Turbina de Pelton, multímetro, cables con conexión de banana, secador de pelo y diferentes leds de colores.

Realización

En esta demostración llevaremos a cabo un experimento donde mediremos el voltaje generado por nuestra turbina, al someterla a la fuerza generada por un fluido ideal (el viento de un secador de pelo), mediante un multímetro. Los resultados muestran que el flujo de aire genera un voltaje que puede alcanzar los 2.50 V aproximadamente. Este voltaje es suficiente para generar una corriente eléctrica por inducción Faraday-Lenz, que se puede visualizar mediante la iluminación de unos leds de colores incorporados al circuito montado para tal fin, ilustrando la conversión de energía mecánica en eléctrica y finalmente luminosa.

Fundamento teórico

En el estudio de este dispositivo consideraremos que el fluido que hará mover la turbina (aire en nuestro caso), es ideal, es decir, incompresible, irrotacional, en régimen estacionario y no viscoso. La energía disponible que tiene el fluido viene dada por su energía cinética de la forma:

    𝐸 = 1/ 2 𝜌𝑉𝑣 2                                                                                        (1)

donde es la densidad del fluido, V el volumen desplazado y v la velocidad a la que se desplaza. Para estimar la energía cedida por el fluido a las palas de la turbina, según el esquema indicado en la figura 1, nos basaremos en el segundo Principio de Newton y en la ecuación de Bernoulli. En primer lugar, la fuerza que el aire hace sobre la pala del rotor es:

        𝐹 = 𝑚𝑎 ≅ 𝑚 ∆𝑣 ∆𝑡 = 𝑚 ∆𝑡 (𝑣𝑖 − 𝑣𝑓)                                                    (2)

donde m es la masa de fluido y ∆𝑣 = (𝑣𝑖 − 𝑣𝑓) es la variación de su velocidad debida a la interacción del fluido con la turbina durante un intervalo de tiempo ∆𝑡, siendo 𝑣𝑖 la velocidad antes de la interacción y 𝑣𝑓 la velocidad después. Utilizando el concepto de velocidad de flujo en masa, definido como la masa de fluido que atraviesa una sección A por unidad de tiempo:

𝑚/∆𝑡 = 𝜌𝐴𝑣                                                                                           (3)

donde 𝑣 es una velocidad media del fluido que es aproximadamente igual a la velocidad de la turbina. Sustituyendo en (2), se tiene

      𝐹 ≅ 𝜌𝐴𝑣(𝑣𝑖 − 𝑣𝑓)                                                                                (4)

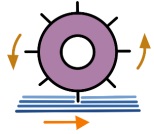
Fig. 1. Transferencia de energía del fluido a la turbina.

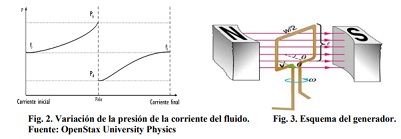
 El flujo de aire se encuentra en su camino una de las palas del rotor de la turbina, lo que provoca un frenado del viento que se traduce en un aumento de presión justo antes de la pala P_a, para caer bruscamente justo después a un valor P_d y recuperarse más tarde hasta la presión normal como se puede ver en la figura 2 [1], donde P_a>P₀ y P_d<P₀, siendo P₀ la presión atmosférica normal lejos de la turbina. Esta diferencia de presiones está directamente ligada a la fuerza ejercida sobre la pala según:

            𝐹 ≅ 𝐴(𝑃𝑎 − 𝑃𝑑 )                                                                              (5)

Sustituyendo (5) en (4) queda: 𝜌𝑣(𝑣𝑖 − 𝑣𝑓) = 𝑃𝑎 − 𝑃_d                                      (6)

Podemos relacionar ahora la diferencia de presiones con las velocidades del fluido antes y después de la interacción aplicando la ecuación de Bernouilli entre la parte anterior y posterior de la pala y un punto alejado de ellas donde la presión es P₀, según:

         1/2 𝜌𝑉𝑣_𝑖 ² + 𝑃₀𝑉 + 𝜌𝑉𝑔ℎ = 1/2 𝜌𝑉𝑣 ² + 𝑃_𝑎𝑉 + 𝜌𝑉𝑔ℎ                        (7)

          1/2 𝜌𝑉𝑣_𝑓 ² + 𝑃₀𝑉 + 𝜌𝑉𝑔ℎ = 1/2 𝜌𝑉𝑣 ² + 𝑃_𝑑𝑉 + 𝜌𝑉𝑔ℎ                        (8)

donde en la ecuación (7) se ha aplicado la ecuación de Bernouilli en la parte anterior de la pala y en la (8) en la parte posterior. Restando a la ecuación (7) la (8), y eliminando el término V, llegamos fácilmente a la siguiente expresión:

          1/2 𝜌(𝑣_𝑖 2 − 𝑣_𝑓 2 ) = 𝑃_𝑎 − 𝑃_𝑑                                                             (9)

Incluyendo la expresión (9) en la (6) se obtiene la velocidad de la turbina como valor promedio de las velocidades del fluido antes y después de interactuar con la misma:

           𝑣 = 1/2 (𝑣_𝑖 + 𝑣_𝑓)                                                                             (10)

Finalmente, la velocidad de rotación de la turbina es 𝜔 = 𝑣/𝑅, siendo R el radio de la misma.

La energía mecánica del fluido cedida a la turbina es aprovechada por ésta para producir electricidad utilizando el fenómeno de la inducción electromagnética, dado que el rotor de la turbina está acoplado a un generador, de manera que aprovecha dicha rotación para generar electricidad tal como ilustra la figura 3. Según la ley de Faraday-Lenz la fuerza electromotriz (f.e.m.) generada es:

              𝜀 = − 𝑑Φ/𝑑𝑡                                                                                 (11)

donde 𝛷 es el el flujo magnético que atraviesa las espiras del generador. Si las espiras están sometidas a un campo magnético constante B, el flujo viene dado por el siguiente producto escalar del campo por el vector superficie A asociado a la espira:

              𝛷 = 𝑩 · 𝑨 = 𝐵𝐴𝑐𝑜𝑠(𝜃) = 𝐵𝐴𝑐𝑜𝑠(𝜔𝑡)                                             (12)

Para un número de espiras N, la fuerza electromotriz generada quedará como:

              𝜀 = 𝑁𝐵𝐴𝜔 sin(𝜔𝑡)                                                                       (13)

i) La turbina se mueve por el flujo del aire del secador. Este flujo debe dirigirse al orificio de la pieza lateral de la turbina, que debe estar encarado a la parte cóncava de las cazoletas o palas. De este modo se consigue aumentar la velocidad del flujo de aire. En principio, esta es suficiente como para poner en marcha la rotación de la turbina.

ii) Una vez conectada la turbina al multímetro (en posición Voltímetro), ir jugando levemente con la dirección del flujo de aire, para comprobar en qué punto la eficiencia es máxima, i.e., el voltaje medido es casi de 2.50 V.

iii) Cuando se conecten los leds a la turbina y se ponga ésta en movimiento generando corriente eléctrica, conviene que el aula esté un poco a oscuras para observar la luz emitida por los leds.

Hay que tener cuidado con la mano que no sujeta el secador, ya que se tiende a colocarla sobre el plástico de la turbina, y éste se calienta bastante debido a la acción del flujo de aire caliente del secador, lo que puede provocar quemaduras si no se está atento.

[1] Cucó Pardillos, S. (2017). Manuel de energía eólica. Desarrollo de proyectos e instalaciones. Universidad Politécnica de Valencia.

[2] Crawford, M. (2012). Lester Allan Pelton. The American Society of Mechanical Engineers [online]. Disponible en: https://www.asme.org/topics-resources/content/lesterallan-pelton (último acceso: 22/07/2020)

1.- La velocidad de la turbina es:

a) Mayor que la velocidad inicial del fluido.

b) Igual que la velocidad inicial del fluido.

c) Menor que la velocidad final del fluido.

d) La semisuma de las velocidades iniciales y finales del fluido.

2.- La fuerza electromotriz producida por el generador es proporcional a:

a) El número de espiras.

b) La velocidad de giro de la turbina.

c) La intensidad del campo magnético.

d) Todas las respuestas son correctas.

3.- Un generador alcanza como máximo 500 V de tensión. Sabiendo que la intensidad del campo magnético es de 0,1 T, que la superficie de una espira es de 0,5 m² y que tenemos 50 espiras, ¿cuál es la velocidad de giro?:

a) 100 rad/s.

b) 150 rad/s.

c) 200 rad/s.

d) 250 rad/s.

4.- Si se triplica la superficie de las espiras del generador:

a) decrecerá la fuerza electromotriz generada con las mismas condiciones. b) requeriremos también del triple de espiras para generar la misma fuerza electromotriz.

c) el giro de las espiras será más rápido.

d) ninguna de las anteriores.