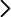- Bloque de madera de ébano (12cm x 4cm x 2,5cm) , masa 70g

- Figura irregular de madera (pino), masa 35g

- Esfera maciza de metal (3 cm de diámetro), masa 40 g

- Caja de metal (12,5 cm de largo)

- Dos trozos de papel de aluminio del mismo tamaño

- Dinamómetro

- Recipiente grande con agua y papel absorbente para secar los objetos.

La madera flota y el metal se hunde.

Mostramos a los alumnos la figura de madera y la esfera de metal y les preguntamos cuál creen que flotará y cuál se hundirá si las colocamos en el recipiente de agua.

Al observar que la esfera se hunde y la figura de madera flota (confirmando su intuición), razonamos una posible explicación relacionada con la masa (la masa m_e de la esfera es algo mayor que la masa m_f de la figura de madera), su tamaño, la composición del material y vemos una idea intuitiva de la densidad.

Cálculo: Usando la definición de densidad:  ρ = m/V   y del volumen de una esfera (conociendo su diámetro D):         V = π D³/6   podemos calcular la densidad de la esfera de metal, siendo mayor que la del agua (1000 kg/m³).

No podemos calcular el volumen de la figura de madera, al ser irregular, y por tanto tampoco su densidad (pero debe ser menor a la del agua para poder flotar)

¿La madera se hunde y el metal flota?

Mostramos ahora el bloque de madera de ébano y la caja de metal y volvemos a preguntar cual flotará y cual se hundirá. Siguen siendo madera y metal, pero el ébano se hunde y la caja de metal flota.

Cálculo: Con la masa del bloque de madera y, midiendo sus dimensiones, podemos calcular su densidad, viendo que es mayor que la del agua (razón por la que se hunde). En cambio, el metal sigue siendo más denso que el agua, pero flota. Razonamos que la forma del metal debe tener algo que ver.

Mostramos dos trozos de aluminio iguales, con uno hacemos una forma similar a la caja de metal y el otro trozo de aluminio lo doblamos por la mitad unas 6 o 7 veces y compactamos. Al colocar cada forma de aluminio en el agua, vemos la forma de barco flota y el aluminio compactado se hunde

Podemos, además, usar la caja de metal que flota e ir colocando en su interior: el bloque de madera de ébano, la figura de madera y la esfera de metal y comprobar que sigue flotando.

Principio de Arquímedes.

Describimos el principio de Arquímedes y el concepto de empuje hidrostático, el cual depende del volumen de fluido V_f desalojado por un objeto sumergido (V_o) en ese fluido. (E = r _f V_f  g)

El empuje que ejerce el fluido sobre el objeto, en sentido ascendente, se opone a la fuerza peso del objeto F_peso. Resulta una fuerza que llamamos Peso aparente: F_{peso_ap} = F_peso – E = 𝑚_o·𝑔 −𝑚_f·𝑔 =𝜌_o·V_o·𝑔 −𝜌_f·V_f·𝑔 = (𝜌_o−𝜌_f)V𝑔       (considerando todo el objeto sumergido V_o = V_f ).

Este objeto sumergido estará sometido a una aceleración según la 2ª Ley de Newton que podemos expresar como:

Así, si el objeto es más denso que el fluido ρo-ρf>0, la aceleración tendrá el mismo sentido que la gravedad y se hundirá (la fuerza peso es mayor que el empuje).

Si el objeto tiene menor densidad que el fluido, ρo-ρf<0, la aceleración tendrá el sentido contrario a la gravedad y flotará (el empuje es mayor que el peso). El objeto que flota asciende hasta que parte de su volumen emerje del fluido, esto hace que el volumen sumergido sea menor, el empuje disminuye y su valor se iguala con el peso.

Medida de la densidad de un objeto con balanza hidrostática.

Usando el concepto de peso aparente, podemos medir el empuje que un fluido ejerce sobre un objeto sumergido en él. Conociendo, además, el peso del objeto y la densidad del fluido, podemos determinar la densidad el objeto.

(objeto sumergido Vo=Vf)

Cálculo: Usamos un dinamómetro para pesar el bloque de madera en seco y obtenemos su peso (F_peso). Lo sumergimos en el agua y medimos con el dinamómetro su peso aparente (F_{peso_ap}). Obtenemos el empuje E =  F_peso – F_{peso_ap}

Conociendo la densidad del agua (ρf= 1000 kg/m³) obtenemos la densidad del bloque de madera que podemos comparar con el valor que obtuvimos al principio, sabiendo su masa y midiendo las dimensiones del bloque.

Secar los objetos para que la madera no se dilate.

No es recomendable hacer una bola con la hoja de aluminio, ya que mantiene aire en su interior y flota en el agua. Es necesario comprimirla bastante para que se hunda.

Serway & Jewet, Física para ciencias e ingeniería. Vol 1. ISBN-13: 978-607-481-357-9

Zanne, Amy E. et al. (2009). Data from: Towards a worldwide wood economics spectrum [Dataset]. Dryad. https://doi.org/10.5061/dryad.234

Ilic, J., Boland, D., McDonald, M., Downes, G. and Blakemore,  P. 2000. Woody density phase - State of knowledge. National carbon accounting system. Technical Report 18 Australian Greenhouse Office, Canberra, Australia.