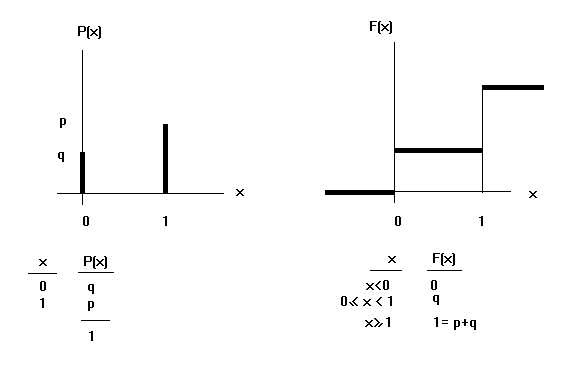
MODELOS DE PROBABILIDAD

MODELOS DE PROBABILIDAD (INTRODUCCIÓN)
MODELOS DISCRETOS
        DISTRIBUCIÓN DICOTÓMICA
        DISTRIBUCIÓN BINOMIAL
        DISTRIBUCIÓN HIPERGEOMÉTRICA
        DISTRIBUCIÓN DE POISSON
        CONVERGENCIA BINOMIAL-POISSON
MODELOS CONTINUOS
       DISTRIBUCIÓN UNIFORME
       DISTRIBUCIÓN EXPONENCIAL
       DISTRIBUCIÓN NORMAL

DISTRIBUCIÓN NORMAL N-DIMENSIONAL ;DERIVADAS DE LA NORMAL (otra lexia)

Una distribución de probabilidad queda definida y caracterizada por:

1.- la especificación de la variable aleatoria y su campo de variación.

2.- la especificación de su asignación de probabilidades, mediante la función de distribución.(Alternativamente mediante la f.cuantía o densidad,la F.C. o la F.G.M.(si existe).(Estas son las FUNCIONES DE DEFINICIÓN)

Si un conjunto dado de distribuciones tiene sus funciones de distribución con la misma ESTRUCTURA FUNCIONAL, diremos que pertenece a la misma FAMILIA DE DISTRIBUCIONES, al mismo MODELO DE PROBABILIDAD o a la misma DISTRIBUCIÓN-TIPO.

p.ej : Todas las distribuciones que están definidas sobre una v.a. continua de modo que para x³ 0 la función de densidad es : f(x)= a e^-ax siendo a un real positivo (alternativamente: F(x)= 1- e^-ax; f (t) = (1-t/a )^-1; son equivalentes la tres caracterizaciones), pertenecen a la misma familia, modelo o tipo (el exponencial).

La estructura matemática de las funciones de definición que caracterizan un modelo de probabilidad suelen depender de uno o más parámetros.Estos parámetros son los PARÁMETROS DE LA DISTRIBUCIÓN(TIPO), y tienen un importancia fundamental, en Estadística matemática y sobre todo en INFERENCIA ESTADÍSTICA.

MODELOS DISCRETOS

Aunque en adelante hablemos de distribución "tal", nos estaremos refiriendo al modelo tal.

Los modelos discretos, son modelos de probabilidad de variable aleatoria discreta.Los más importante son los modelos de BERNOUILLI (especialmente "la distribución binomial") y la "distribución de Poisson".

1.- DISTRIBUCIÓN DICOTÓMICA.(Bernouilli).

El campo de variación de la variable es : {0,1}. y la función de cuantía es :

P(X=0) = q = 1-p

P(X=1)= p .

Si una variable aleatoria X sigue o tiene una distribución dicotómica de parámetro p se expresa como X ~ D(p).

Modeliza situaciones en las que :

· Se realiza una prueba

· Que sólo puede dar dos resultados posibles: A y A

· La probabilidad del resultado A es P(A) = p y la del resultado A es P(A)= q=1-p.

· En estas circunstancias la variable aleatoria X significa "nº de resultados A que se obtienen.

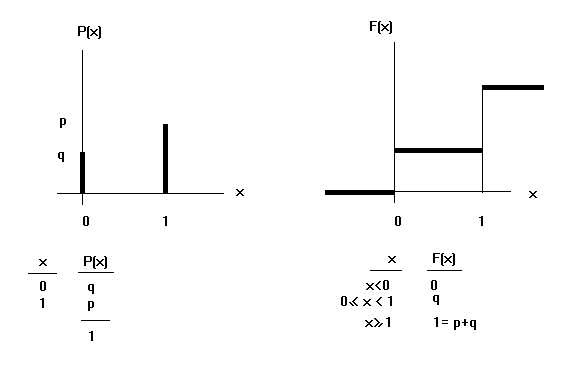
La media de la distribución será: m = å x P(x) = 0.q + 1.p = p

La varianza de la distribución: s² = a₂- m²

con : a₂ = S x².P(x) = 0.q +1.p= p

s² = a₂- m² = p - p² = p (1-p) = p.q

Y la F.G.M.:

f (t) = E(e^tx) = S e^tx P(x) = e⁰ q + e^t p = (pe^t +q)

Es fácil comprobar que todos los momentos ordinarios de orden mayor o igual a 1 son iguales a p.

2.- DISTRIBUCIÓN BINOMIAL.

El campo de variación de la variable es {0,1,2,3,..., n} y la función de cuantía es:

para valores de x= 0,1,2,...n siendo nÎ N , p Î [0,1] y q=1-p

Si una variable aleatoria, X, sigue una distribución binomial de parámetros n y p se expresa como: X ~ B(n,p).

Situaciones que modeliza:

· Se realiza un número n de pruebas (separadas o separables).

· Cada prueba puede dar dos únicos resultados A y Ã

· La probabilidad de obtener un resultado A es p y la de obtener un resultado à es q, con q= 1-p, en todas las pruebas.Esto implica que las pruebas se realizan exactamente en las mismas condiciones.Si se trata de extracciones, (muestreo), las extracciones deberán ser con devolución (reemplazamiento) (M.A.S).

· En estas circunstancias se aleatoriza de forma que variable aleatoria signifique:

X = nº de resultados A que se obtienen en las n pruebas

Es fácil comprobar que considerando estas condiciones la función de cuantía de la variable es precisamente la que se ha especificado arriba.

La función de distribución quedará como F(x) = S P(x), sin una expresión analítica concreta.

Los indicadores-momentos (media y varianza) pueden obtenerse a partir de la función de cuantía (operador esperanza) o a a partir de F.G.M.:

F.G.M.: f (t) = E(e^tx) = S e^tx P(x) =

(desarrollo del Binomio de Newton)

f (t) =(pe^t + q)ⁿ

A partir de aquí :

la media m = a₁= f '(t=0) :

f '(t)= n (pe^t + q)^n-1pe^t ¾ ¾ ® f '(t=0) = n(p+q)^n-1 p = n.1.p= np

la varianza s² = a₂- m² y a₂ =f ''(t=0)

f ''(t) = n.(n-1) (pe^t + q)^n-2pe^t pe^t+ n (pe^t + q)^n-1 p ¾ ¾ ®

¾ ¾ ® f ''(t=0) = n.(n-1) (p + q)^n-2p² +n (p+q)^n-1 p =

=n.(n-1)p² + np = n²p² -np² + np

a₂ =n²p² -np² + np

de donde : la varianza s² = a₂- m² =n²p² -np² + np -(np)² =-np² + np =

s² =np(1-p)= npq

Análogamente se pueden obtener los coeficientes de Asimetría y de Curtosis.

que acaban siendo:

Es interesante hacer ver que si p=q= 0.5 la distribución es SIMÉTRICA Y TIENE VARIANZA MÁXIMA

Puede determinarse la moda de una distribución binomial como el (los) valor(es) de la variable (número entero del 0 a n) que verifica:

pn - q £ Mo £ pn + p

Generalmente será un único valor ( la parte entera de la media), y podrán ser dos valores modales cuando pn +p ( ó pn-q) sea un número entero[p.ej. B(5,0.5)]

3.DISTRIBUCIÓN HIPERGEOMÉTRICA

Dada la siguiente situación:

• Una población constituida por N individuos en total.
• De los cuales Np individuos son del tipo A , y Nq individuos son del tipo Ã.

De forma que la proporción de individuos A que hay en la población es p, y la proporción de individuos de tipo à , es q (p+q=1).

• Se realizan n (pruebas) extracciones sin reemplazamiento

De forma que la probabilidad de extraer un individuo A ( Ã) en una de las extracciones depende de los resultados de las pruebas anteriores.

• Si consideramos la variable aleatoria X = nº de resultados A obtenidos en las n extracciones , X seguirá una distribución hipergeométrica. X~H(N,n,p)

Puede comprobarse que la función de cuantía es, entonces:

La distribución hipergeométrica es semejante a la binomial, excepto en el hecho de que las pruebas no mantienen constantes las probabilidades de A y Ã

al término (N-1/(N-n)) se le llama coeficiente de exhaustividad ,o también, factor corrector de poblaciones finitas :

Puede observarse que este factor es siempre inferior a 1 y que cuando la población es muy grande (N® ¥ ) tiende a 1(por tanto si la población es muy grande la media y la varianza coinciden con las de la D. Binomial).

De hecho, si la población es muy grande (resulta irrelevante la existencia o no de reposición) la función de cuantía de la Hipergeométrica tiende a la f. de cuantía de la distribución Binomial y se puede prescindir del hecho de que haya o no reemplazamiento.

4. DISTRIBUCIÓN DE POISSON

Formalmente : dada una variable aleatoria X con campo de variación

X Î {0,1,2,..., ¥ }, es decir X Î N cuya función de cuantía sea:

siendo l un parámetro positivo

diremos que X sigue una distribución de Poisson de parámetro l , X ~ P(l ).

Situaciones que modeliza:

• Se observa la ocurrencia de hechos de cierto tipo durante un período de tiempo o a lo largo de un espacio, considerados unitarios
• El tiempo (o el espacio) pueden considerarse homogéneos, respecto al tipo de hechos estudiados, al menos durante el período experimental; es decir, que no hay razones para suponer que en ciertos momentos los hechos sean más probables que otros.
• En un instante (infinitesimal) sólo puede producirse como mucho un hecho (se podrá producir o uno o ninguno).
• La probabilidad de que se produzca un hecho en un intervalo infinitesimal es prácticamente proporcional a la amplitud del intervalo infinitesimal.

Si en estas circunstancias la variable aleatoria X = nº de hechos que se producen en un intervalo unitario sigue una distribución de Poisson , que cómo veremos tendrá por parámetro l el número medio de hechos que pueden producirse en el intervalo unitario.

F.G.M. de una distribución de Poisson:

f (t) = E(e^tx) = S e^tx P(x) = = =

Derivando sucesivamente podremos obtener los distintos momentos ordinarios y, a partir de ellos media, varianza y otros indicadores:

f ' (t) = l e^t e^{l(et - 1)} ¾ ¾ ¾ ® f ' (t =0) = a₁= m = l

f '' (t) = l e^t e^{l(et - 1)} +( l e^t )² e^{l(et - 1)} ¾ ¾ ¾ ®

¾ ¾ ¾ ® f ' (t =0) = a₂= l + l²

de forma que la varianza será: s² = a₂- m² = l + l² - l² = l

La moda de una distribución de Poisson puede determinarse como el valor de la variable (el número natural) que verifica que:

l - 1 £ Mo £ l

Habitualmente la moda será la "parte entera de la l (de la media)" , pero habrá dos modas (l - 1 y l ) cuando l sea un número entero.

PROPIEDAD IMPORTANTE: CONVERGENCIA BINOMIAL-POISSON.

Dada una variable aleatoria X que siga una distribución Binomial si el parámetro n es muy grande (n ® ¥ ) y el parámetro p es muy pequeño (p ® 0 ) su distribución puede aproximarse por la de una de Poisson con parámetro l = np.

la f. de cuantía de una variable X / X ~ B(n,p) cuando n ® ¥ y p ® 0 tiende a:

de forma que haciendo l = np tiende a la f. de cuantía de una distribución de Poisson con l = np.

MODELOS CONTINUOS

1.DISTRIBUCIÓN UNIFORME (DE V.CONTINUA)

Dada una variable aleatoria continua, X , definida en el intervalo [a,b] de la recta real, diremos que X tiene una distribución uniforme en el intervalo [a,b] cuando su función de densidad sea: X ~ U([a,b])

f(x)= 1/(b-a) para x Î [a,b].

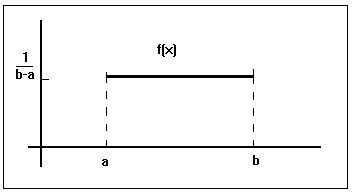
De manera que la función de distribución resultará:

0 para x < a

1 para x ³ b

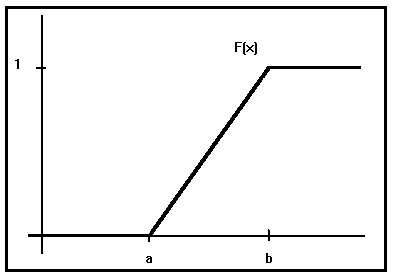
Es fácil comprobar que m =(b+a)/2 y que s² = (b-a)²/12

2. DISTRIBUCIÓN EXPONENCIAL

Dada una variable aleatoria continua, X , definida para valores reales positivos.

diremos que X tiene una distribución exponencial de parámetro a cuando su función de densidad sea: f(x) = a e^{-a x} para x ³ 0 ( siendo el parámetro a positivo)

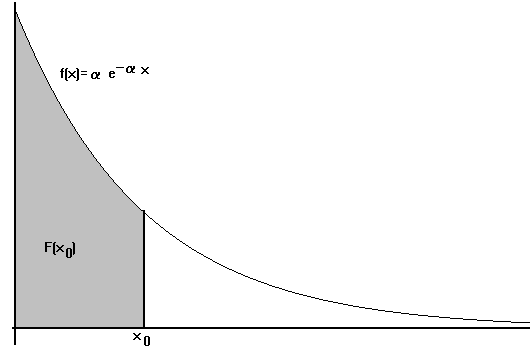
La función de distribución será

F(x) = {	=0 para x < 0

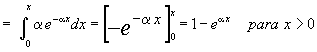F.G.M.

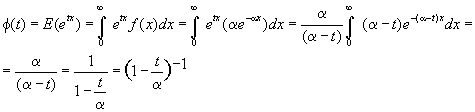
Si derivamos la F.G.M. en el punto t=0 obtendremos que m = 1/a

Y derivando por segunda vez en t= 0 obtendremos el momento ordinario de segundo orden, y a partir de él la varianza: s ²= 1 /a²

la moda es 0 y la mediana ln2/a

3.DISTRIBUCIÓN NORMAL (ir a distribucción normal)

La distribución normal es la más importante de todas las distribuciones de probabilidad.Es una distribución de variable continua con campo de variación [-¥ ,¥ ], que queda especificada a través de dos parámetros ( que acaban siendo la media y la desviación típica de la distribución).

Una variable aleatoria continua, X, definida en [-¥ ,¥ ] seguirá una distribución normal de parámetros m y s , ( X ~ N(m ; s ) ) , si su función de densidad es :

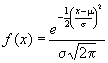para x Î [-¥ ,¥ ]

cuya representación gráfica es:

Importancia de la distribución Normal.

a) Enorme número de fenómenos que puede modelizar: Casi todas las características cuantitativas de las poblaciones muy grades tienden a aproximar su distribución a una distribución normal.

b) Muchas de las demás distribuciones de uso frecuente, tienden a distribuirse según una Normal, bajo ciertas condiciones.

c) (En virtud del teorema central del límite).Todas aquellas variables que pueden considerarse causadas por un gran número de pequeños efectos (como pueden ser los errores de medida) tienden a distribuirse según una distribución normal.

La probabilidad de cualquier intervalo se calcularía integrando la función de densidad a lo largo de ese de intervalo, pero no es necesario nunca resolver la integral pues existen tablas que nos evitan este problema.

F.G.M.:puede probarse que la función generatriz de momentos de una distribución N(m ; s ) es:

f (t) = E(e^tx) = e(^{m t + ½ s2t2})

A partir de ella es fácil comprobar como efectivamente la media de la distribución es el parámetro m y, cómo su varianza es el parámetro s .

Igualmente puede comprobarse que la distribución es simétrica y que su curtósis es nula.

Propiedad importante: "CUALQUIER TRANSFORMACIÓN LINEAL DE UNA VARIABLE ALEATORIA NORMAL TIENE TAMBIÉN UNA DISTRIBUCIÓN NORMAL DONDE LA MEDIA DE LA NUEVA VARIABLE ES LA MISMA TRANSFORMACIÓN LINEAL DE LA MEDIA DE LA ANTIGUA Y DONDE LA DESVIACIÓN TÍPICA ES LA DESVIACIÓN TÍPICA ANTIGUA MULTIPLICADA POR EL COEFICIENTE ANGULAR DE LA TRANSFORMACIÓN":

Dada una variable X ~ N(m ; s ) si la nueva variable Y es Y = a+bX

Y~ N(a+bm ; bs ) :

en efecto: la F.G.M de la distribución de X será:

E(e^tx) = e(^{m t + ½ s2t2})

y la F.G.M. de la distribución de Y será:

fy(t)= e^at.f_x(bt) = e^at .e(^{m bt + ½ s2b2t2}) = e(^(a+bm )t + (bs )²t²)

que es la F.G.M de una distribución N(a+bm ; bs ) //*q.e.d.*//

Consecuencia importante de esto es que si se tipifica una variable X / X ~ N(m ; s ) la nueva variable Z = tendrá una distribución N(0,1).

La distribución N(0,1) se conoce con el nombre de Normal tipificada o reducida y tiene una importancia teórica y práctica fundamental.Su Función de distribución está tabulada y ello nos permite calcular directamente cualquier probabilidad de cualquier intervalo de cualquier distribución normal ( X ~ N(m ; s )), sin necesidad de integrar.

En efecto: si X ~ N(m ; s ) y queremos calcular P(XÎ [a,b])==P(a£ X £ b) =

donde F es la F. de distribución de una Normal tipificada, que puede evaluarse a través de las tablas.