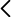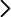Recipiente, agua, dinamómetro, báscula, objeto problema (pesa de bronce).

La balanza hidrostática mide el empuje que un fluido ejerce sobre un cuerpo inmerso en él y permite determinar la densidad de ese cuerpo basándose en el principio de Arquímedes. Se utiliza tanto un dinamómetro como una báscula, que realizan una medida del peso del cuerpo en el aire y al introducirlo en un fluido, en este caso agua.

Demostración cualitativa con dinamómetro o báscula:
Al colgar el cuerpo del dinamómetro en aire medimos la fuerza gravitatoria (o peso 𝑃𝑔): por ejemplo, 𝑃𝑔=4,9 N. Ahora repetimos sumergiendo el cuerpo completamente en agua, de forma que no toque el fondo o las paredes. El dinamómetro indica una fuerza menor de 4,3 N.
Igualmente, podemos usar la báscula: colocamos el vaso con agua sobre la báscula y taramos. Apoyamos
el cuerpo también sobre la báscula y medimos su masa 𝑚𝑐=496,7 g. Pero al introducirlo completamente
en el agua, colgando de un hilo, la báscula indica una masa menor, de 60,2 g.

EXPLICACIÓN 1. Medida de la densidad con el dinamómetro: Al introducir el cuerpo en el fluido (agua), actúa la fuerza empuje hidrostático, que coincide con el peso del fluido desalojado al introducir el sólido: 𝐸 = 𝑚𝑓 𝑔 = 𝜌_𝑓 𝑉_𝑓 𝑔
El empuje es de sentido opuesto al peso y se debe a la variación de la presión del fluido sobre el objeto con la profundidad, mayor en la parte inferior que en la superior (en agua, por cada 10 m de profundidad, la presión aumenta en 1 atmósfera).
La fuerza resultante 𝑃𝐿 = 𝑃𝑔 − 𝐸 es vertical (en este caso con sentido hacia abajo y menor que el peso).
𝑃𝐿 = 𝑃𝑔 − 𝐸 = 𝜌_𝑐 𝑉_𝑐 𝑔 − 𝜌_𝑓 𝑉_𝑓𝑔  Los subíndices ‘c’ y ‘f’ hacen referencia al cuerpo y al fluido respectivamente. El objeto debe estar totalmente sumergido para que sea cierta la consideración de que 𝑉𝑐 = 𝑉𝑓. El cociente entre el peso en aire 𝑃𝑔 y E (diferencia entre pesada en aire y en agua)
proporciona directamente la densidad específica del cuerpo (respecto a densidad del fluidla o, agua en este caso). La densidad del agua 𝜌𝑓 ≈ 1 g/cm ³, luego el cociente entre peso y empuje es prácticamente la densidad del cuerpo en g/cm3).
Para el objeto problema incluido en la demo, se han obtenido las siguientes medidas y resultados, incluyendo las incertidumbres:

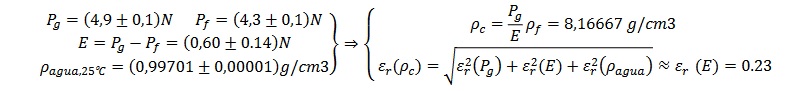
Luego 𝜌𝑐 = (8,2 ± 1,9) 𝑔 /𝑐𝑚𝑚³ , que coincide con la densidad de una aleación de bronce (entre 7,4 y 8,9 g/cm ^3, ver tabla)
Como se puede ver, el error relativo que predomina es el del empuje. Por tanto, cuanto mayor sea este, menor incertidumbre tendrála densidad del cuerpo. En este caso el error relativo de la densidad es superior al 20%, pero se podría reducir realizando medidas con un dinamómetro de mayor sensibilidad.

EXPLICACIÓN 2. Medida de la densidad con una báscula:
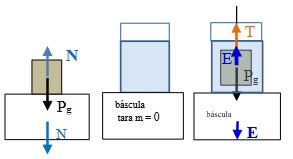
1. La báscula mide la fuerza de contacto N que aplica el cuerpo sobre ella (igual y opuesta a la que la báscula aplica al cuerpo).
En equilibrio, 𝑁 = 𝑃𝑔 = 𝑚𝑐 𝑔 = 𝜌𝑐 𝑉𝑔 . La báscula generalmente está calibrada en kg y mide la masa del cuerpo, es decir:
𝑁/𝑔 = 𝑚𝑐 =𝜌𝑐 𝑉. Coloco el objeto sobre ella y la báscula marca 𝑚𝑐= 496,7 g.
2. Coloco el vaso con agua sobre la báscula y la taro para que marque 0 gramos. La medida de N/g anterior también se puede
hacer apoyando el objeto sobre el vaso tras haber tarado, o apoyado en el fondo, dentro del vaso con agua.

3. Ahora suspendo el objeto del hilo: sujetando por un extremo, lo sumerjo completamente en el vaso, evitando que toque el fondo o las paredes. En este caso sobre el cuerpo actúa la fuerza gravitatoria 𝑃𝑔, la tensión del hilo 𝑇 y el empuje 𝐸 del agua sobre el cuerpo, de forma que en equilibrio, 𝑇 = 𝑃 − 𝐸. Además, el cuerpo ejerce una fuerza 𝐸 igual y opuesta sobre el agua que es la que mide la báscula. En nuestro caso E/g = 𝑚agua =agua · V = 60,2 g.

La relación entre N 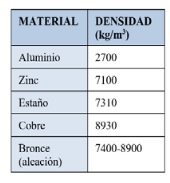y E proporciona la densidad relativa del
objeto respecto a la del agua:

Por lo tanto

Si se realiza el análisis de errores, se obtiene finalmente
ρ = 8,251±0,014 g/cm ³, compatible con una pieza de bronce.
En este caso, el error relativo es mucho menor (<0,2%).

Nota histórica: La historia popular sobre Arquímedes cuenta que salió corriendo desnudo por la ciudad de Siracusa, gritando ¡Eureka!, tras dar con la solución, mientras se daba un baño, al problema que el rey Hierón le había planteado para saber si era víctima de una estafa: determinar si la corona de oro encargada a un orfebre era realmente de oro o una amalgama. El aumento del nivel del agua y su desbordamiento cuando se introdujo en la bañera habría inspirado a Arquímedes el método para resolverlo. Esta leyenda se debe a Vitruvio y no hace justicia al elevado nivel científico de los trabajos de Arquímedes. Su tratado Sobre loscuerpos flotantes analiza (libro I) los principios hidrostáticos generales y (Libro II) la estabilidad de diferentes secciones de paraboloide en un fluido (secciones de navíos). Se sabe, además, que Arquímedes contribuyó al diseño de la nave Siracusia (un Titánic de la época que contenía jardines, biblioteca, termas, y una gigantesca catapulta en cubierta- lo que requería especial estabilidad), supervisó su construcción e ideó un sistema mecánico que permitía la botadura empleando una sola mano. Galileo Galilei, 19 siglos después, se dio cuenta de que esta leyenda no podía ser cierta, al estudiar los tratados de Arquímedes y comprobar el sofisticado nivel de sus contenidos. A partir de ellos, Galileo reconstruyó los principios hidrostáticos que el propio Arquímedes habría usado si hubiera tenido que discernir la composición de dos cuerpos de igual peso y diferente densidad, y los recogió en La Bilancetta. (La pequeña balanza). El eminente historiador de la ciencia Alexander Koyré, de hecho, consideró que la revolución científica del s. XVI consistió en la admisión y gradual comprensión de la obra de Arquímedes.
La idea es la siguiente: dos cuerpos en aire con la misma masa (y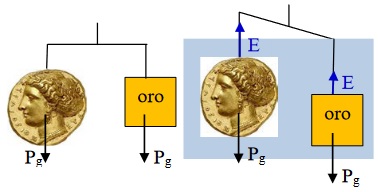 peso Pg) se equilibran en la balanza. Pero si al introducir el conjunto en agua dejan de estar en equilibrio, significa que el empuje no es el mismo sobre
ambos. En la figura, el empuje sobre la moneda es mayor, luego desaloja mayor masa y volumen de agua que la pieza de oro. Por lo tanto, su densidad es menor (hay que concluir que está amalgamada con otro metal). La densidad se puede cuantificar experimentalmente sin necesidad de conocer, y esto es lo importante, el volumen del cuerpo.

• La idea básica es que a partir de dos medidas con un dinamómetro (peso en aire y peso con objeto sumergido en agua), se obtiene la densidad de un objeto sin necesidad de conocer su volumen. Dependiendo del tiempo disponible, se puede dedicar tiempo al cálculo de errores, o bien saltarse este paso.
• Se puede utilizar otro líquido de distinta densidad para observar que el valor de la densidad del objeto es el mismo pero su peso aparente cambia en función del fluido utilizado. De hecho a partir del peso en aire y de los dos pesos aparentes (por ejemplo en agua y alcohol) es posible calcular tanto la densidad del cuerpo como la del otro fluido.
• Esta demo está relacionada con la Demo 36 (Balanza hidrostática de Mohr), que se aconseja abordar a continuación.

El cuerpo debe quedar totalmente sumergido (sin tocar paredes laterales y ni el fondo del recipiente).Usar a continuación la demo 36 de la balanza de Mohr https://fisicademos.blogs.uv.es/files/2017/07/demo36.pdf

http://www.sc.ehu.es/sbweb/fisica3/fluidos/densidad/densidad.html

Los tratados de Arquímedes (ed. T. L. Heath, CUP 1897)). Sobre los cuerpos flotantes (p 252)

https://archive.org/details/worksofarchimede00arch/page/252/mode/2up

Chantal Ferrer roca y Andrea Bombi “La revolución olvidada, aspectos lingüísticos de una pérdida y recuperación. Reflexiones sobre un ensayo de Lucio Russo” https://roderic.uv.es/handle/10550/27386