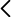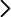La esfera de Hoberman y los pulsares

Categorias:

Mecánica.

Autores:

chantal maria ferrer roca, Asunción Marco, Maria Dolores Zaragozá

Etiquetas:

Rotación, Conservación del momento angular, Momento de Inercia, Púlsares.

Objetivos:

Demostrar la conservación del momento angular cuando varía el momento de inercia de la esfera porque ésta cambia su radio mediante un mecanismo interno, en analogía con lo que sucede a las estrellas que se transforman en púlsares.

Materiales:

Esfera de Hoberman, esfera geodésica articulada con polea e hilo para contraerla a voluntad

Tiempo de montaje:

2 minutos.

Descripción:

Descripción
La esfera de Hoberman es una esfera articulada que puede aumentar y disminuir su tamaño mediante un mecanismo
interno que consiste en un hilo que pasa por una pequeña polea. La dirección del hilo coincide con el eje de giro de la
esfera.
Poner a girar la esfera completamente abierta (figura 1), y a un cierto punto tirar del hilo hacia abajo para que la esfera
se contraiga (figura 2). Observamos que al reducirse el radio de la esfera, su velocidad de giro aumenta de forma
apreciable. Si de nuevo soltamos el hilo para que se expanda, se reduce la velocidad de giro.

Explicación
El momento de fuerzas externo sobre la esfera es nulo. Las fuerzas que actúan sobre la esfera (tensión del hilo superior,
fuerzas gravitatoria y fuerza aplicada con la mano para contraerla, están aplicadas al eje de giro, y por lo tanto su
momento de fuerzas es nulo. Por lo tanto, se conserva el momento angular del sistema.
Al modificar su radio, cambiamos su momento de inercia. Cuando la esfera está con su radio máximo, totalmente
expandia, tiene un momento de Inercia Ie y cuando la esfera está totalmente contraída tiene un momento de inercia Ic <
Ie ya que el radio es ahora menor. Como el momento angular es L=Iω, y permanece constante, tanto en módulo como
en dirección (esta es vertical, usando la regla de la mano derecha, hacia arriba o abajo según el sentido de giro):

𝐿𝑐 = 𝐼𝑐 𝜔𝑐 = 𝐼𝑒 𝜔𝑒 = 𝐿𝑒

Luego la velocidad angular cuando está contraída es mayor: $\large \omega _{c=\frac{I_{e}}{I_{c}}}\omega _{e}> \omega _{e}$

Podemos analizarlo cuantitativamente: Cuando la esfera está expandida podemos suponer que es una superficie esférica
o esfera hueca de radio 𝑅𝑒 , cuyo momento de inercia es $\large I_{e}=\frac{2}{3}MR_{e}^{2}$ .Cuando está contraída se asemeja más a una
esfera maciza de radio 𝑅𝑐 , cuyo momento de inercia es $\large I_{c}=\frac{2}{5}MR_{c}^{2}$ .
Luego: $\large \omega _{c}=\frac{I_{e}}{I_{c}}\omega _{e}\approx \frac{5R_{e}^{2}}{3R_{c}^{2}}\omega _{e}$

Para nuestra esfera se mide que 𝑅𝑒 = 38,1 𝑐m 𝑦 𝑅𝑐 = 12,07 cm. Luego el valor teóricode la relación entre velocidades angulares es, aproximadamente: $\large \frac{\omega _{c}}{\omega _{e}}=\frac{5R_{e}^{2}}{3R_{c}^{2}}=\frac{72,6}{4,4}=16,6$

Este valor hay que comparalo con el experimental, midiendo el tiempo que la esfera tarda en dar varias vueltas en las
dos situaciones.

Comentarios:

Esta demostración puede utilizarse para visualizar los cambios que se producen en la velocidad de rotación alrededor de su eje de las estrellas a lo largo de su evolución. Y en particular la transformaciónde ciertas estrellas muy masivas o supernovas en estrellas de neutrones o púlsares, de radio muy pequeño y periodos de rotación estremadamente rápidos: la contracción extrema de la materia para radios muy pequeños conlleva un aumento, en la misma proporción, de la velocidad angular(disminución del periodo de rotación).

Advertencias:

Procurar que el hilo del mecanismo interior que contrae la rueda pase sin torcerse por el interior de la garganta de la polea del mecanismo de contracción.

Bibliografía:

Using an Expandable Toy in Discussing Rotational Motion

The Physics Teacher 43, 247 (2005); https://doi.org/10.1119/1.1888088

Ficha:

Demo 183 en pdf