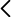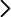Sujetar la varilla roja por la empuñadura en posición vertical u horizontal. Mover la muñeca para hacerla girar rápidamente en vaivén como aparece en la imagen superior. Hacer lo mismo con la azul: se nota que nos cuesta mucho más y no conseguimos hacerlo con la misma velocidad. Puedes coger una varilla en cada mano para comparar el efecto al mismo tiempo.
Explicación
Los cuerpos presentan una inercia frente a los giros que depende de cómo se encuentra distribuida su masa alrededor del eje de giro (momento de inercia). La ecuación dinámica para los giros establece que la aceleración angular a con la que gira un cuerpo depende momento de fuerzas neto τ que actúa sobre él, dividido por el momento de inercia I.
De forma que si aplicamos el mismo momento de fuerzas o torque a dos cuerpos con momentos de inercia I1 e I2 > I1 las aceleraciones angulares serán α1=τ / I1 α2=τ / I2 < α1.
En este caso, las dos varillas tienen la misma masa, pero distribuida de forma diferente, una cerca del centro de giro (roja) y la otra en los extremos (azul). Y para esta segunda notamos que la aceleración angular que conseguimos es menor, aplicando con la mano un torque parecido (es más difícil aumentar su velocidad rotación o disminuirla cuando tiene un valor constante).
El momento de inercia de una masa puntual m situada a una distancia d del eje de giro viene dado por 
.
Suponiendo que la varilla es un tubo de una cierta masa mt y momento de inercia It al que se añaden dos masas puntuales a pocos centímetros del centro de la empuñadura en un caso y en los extremos en el otro entonces, los momentos de inercia de las varillas serán 
. Supondremos que 
.
Entonces, 
y, en el caso de que It sea despreciable, 
