Saltar la navegación

Introducció al modelatge de barres

Què és el modelatge de barres?

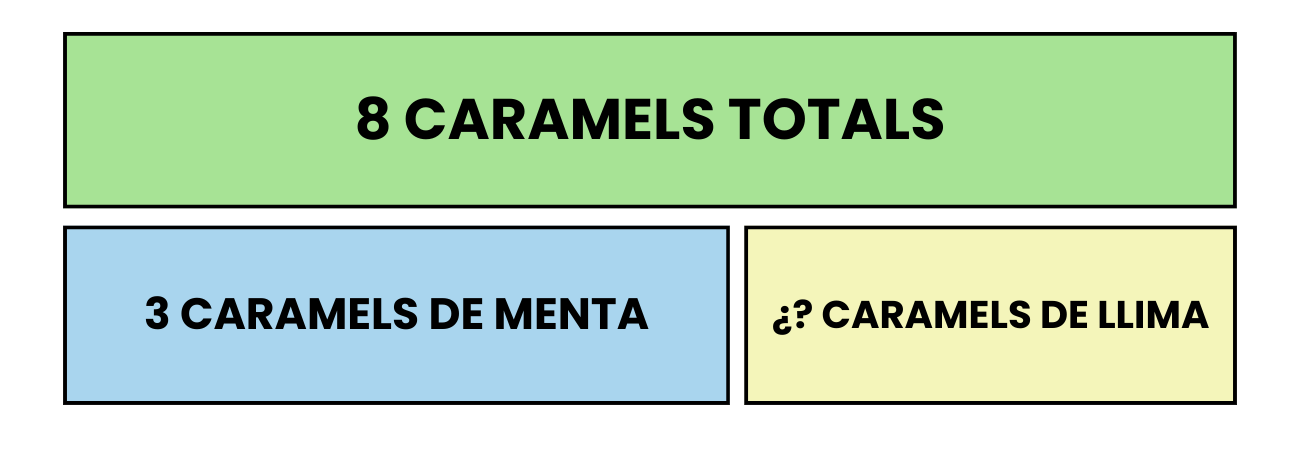
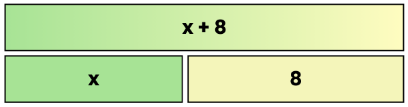
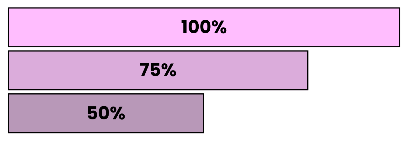
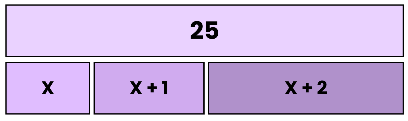
És un model pel qual podem representar, mitjançant l'ús de barres, les quantitats i les relacions que tenen aquests dins d'un problema.

S'utilitza com a ferramenta matemàtica visual dibuixant rectangles, coneguts com barres a fi de facilitar la comprensió, representació y resolució de problemes d'una forma gràfica i estructurada.

Per exemple: Maria ha comprat 3 taronges i 4 pomes. Anem a veure com es representaria amb aquest mètode.

Elaboració pròpia. Figura 1. (CC0)

Importància de l'ús d'aquest model

La seua eficàcia és gràcies al traspaç del llenguatge verbal a una estructura visual organizada, ajudant a establir una base sòlida per a l'adquisició de competències matemàtiques més complexes. Amb açò, es permet:

  • Per una banda, s'identifica quantitats conegudes i desconegudes dins d'un problema.

Oriol té 8 caramels en total. En té 3 de menta. Quants en té de llima?

En la imatge, s'observen tres barres. En la part superior hi ha una barra verda que abasta els caramels totals que té Oriol, amb un total de 8 caramels. Baix d'aquesta, es representen dues barres proporcionals en funció de la quantitat: una blava que representa els caramels de menta, que són 3 i una barra groga, que representa els caramels de llima i quina xifra és desconeguda.

                  Elaboració Pròpia. Figura 2. Representació visual en barres d'un problema. (CC0)

  • A més, permet identificar de forma visual les relacions de comparació, totalitat i parts o canvi de les dades.

    1. COMPARACIÓ: Es pot dur a terme procediments que impliquen diferenciar i comparar dos o més dades. 

    2. TOTALITAT: Es poden sumar varies parts i juntar-les com un tot.

    3. PARTS: També s'utilitza per treballar fraccions o porcions d'un tot. 

  • També facilita l'escolliment de l'operació matemàtica corresponen necessària per resoldre els problemes. 

Usos segons el nivell educatiu

Gràcies a la seva simplicitat i versatilitat, aquesta metodologia pot utilitzar-se en tots els nivells educatius, inclós aplicar-lo en casos on hi ha necessitats especials de suport educatiu.

EDUCACIÓ INFANTIL EDUCACIÓ PRIMÀRIA I SECUNDÀRIA ADAPTABILITAT NESE

S'utilitza amb materials manipulatius representant problemes senzills com: Tinc 4 galletes i em menge 1. 

Materials d'interés:

  • Snapcubes o cubs manipulatius. 

  • Caixes de barres. 

S'utilitza per dur a terme equacions algebraiques o problemes de proporcionalitat. 

  • Representació en barres d'equacions: 

  • Representació en barres de proporcionalitat: 

És ideal per a estudiants amb dificultats de processament verbal, ja que canvia les paraules a imatges. 

Per exemple: 

La suma de tres nombres consecutius és igual a 25. Quins són?

Per què és eficaç el modelatge de barres?

  • Redueix la càrrega cognitiva: Observar un problema de forma gràfica i visual, possibilita a l'estudiant focalitzar-se en el procediment lògic i no en retindre dades.
  • Fomenta el pensament crític: Cal que s'analitzen les relacions entre les quantitats abans de fer les operacions i no actuar de forma impulsiva. 
  • Presenta capacitat d'adaptació: Serveix per a problemes simples com complexos (fraccions, per exemple).

Creado con eXeLearning (Ventana nueva)