El modelo anterior es un modelo de distribución de probabilidad. Hay modelos de distribuciones de probabilidades de variables aleatorias discretas y de variables aleatorias continuas. A continuación se introduce el modelo de distribución Binomial:

La forma general del modelo es

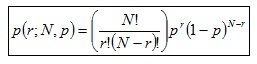
donde

p: probabilidad de ocurrencia de un suceso.

r: Número de ocurrencias del suceso cuya probabilidad queremos obtener.

 

Ejemplo

La probabilidad de obtener 5 aciertos respondiendo al azar en un examen que consta de 10 cuestiones, cada una con 4 alternativas, es:

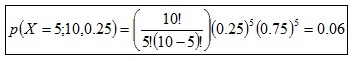
El modelo Binomial se aplica a variables que presentan las siguientes características:

a) Son variables dicotómicas (presentan solo dos modalidades, como sexo) o dicotomizados (presentan más de dos modalidades pero han sido agrupadas a dos. Ejemplo: Agrupación en las categorías "solteros" y "otros" de las modalidades "soltero, casado, divorciado, viudo" de la variable "Estado Civil").

b) "r" representa el número de ocurrencias del suceso cuya probabilidad se desea.

c) La forma de la distribución se acerca a la Normal como mayor sea N. Ejemplo con N= 100, r= 10 y p= 0.5:

 

Ejemplo

Obtención de la distribución de la variable "puntuación en una prueba objetiva cuando las respuestas se emiten al azar". Aplicamos el modelo a todos los posibles valores de X y obtenemos las probabilidades de los valores de la variable. Estos valores son 0, 1, 2, . . . , 10 (número de aciertos posibles en una prueba de 10 cuestiones). La función de probabilidad (conjunto de valores con sus probabilidades) es:

(Puedes activar la hoja clicando una vez; al aparecer el cuadro, clica dos veces más. Puedes variar los datos, como p(x) y comprobar qué efecto tiene variar el número de alternativas en las probabilidades, la Esperanza, la función de distribución etc.)

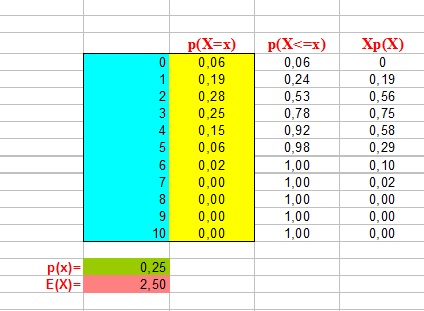
(El número esperado de aciertos al azar es igual a 2.5)