# Definir el número de lanzamientos
n_lanzamientos <- 1000
# Simular los resultados de los lanzamientos
set.seed(33)
resultados_lanzamientos <- rbinom(n = n_lanzamientos, size = 1, prob = 0.5)6 Técnicas de simulación
6.1 Introducción
Las técnicas de simulación se erigen como otro componente fundamental para el análisis prospectivo, ya que permiten modelar el comportamiento de sistemas complejos y analizar diferentes escenarios y políticas en un entorno simulado. La simulación implica la construcción de un modelo que representa, por un lado, las variables y relaciones importantes de un sistema y, por otro lado, la realización de simulaciones para observar cómo se comporta el sistema en diferentes situaciones.
Existen diferentes técnicas de simulación, cada una de las cuales tiene sus propias ventajas y desventajas. Por ejemplo, la simulación de Monte Carlo se utiliza comúnmente para modelar la incertidumbre y proporcionar una distribución de probabilidad de los resultados, mientras que la simulación basada en agentes se utiliza para modelar la interacción entre diferentes agentes en un sistema.
Si bien es cierto que existen diferentes técnicas de simulación, como comentaremos a continuación, en esta sesión nos centraremos en la técnica de simulación de Monte Carlo, puesto que es la más utilizada.
Para finalizar la sesión, y con el objetivo de afianzar los conceptos teóricos abordados, se mostrarán algunos ejemplos sobre cómo aplicar técnicas de simulación implementando el software estadístico R.
6.2 Técnicas de simulación
Como hemos adelantado en la introducción, existen diferentes técnicas de simulación. Algunas de ellas son las siguientes:
Simulación de Monte Carlo. Esta técnica es una herramienta muy poderosa para simular escenarios aleatorios. En esta técnica, se utilizan números aleatorios para simular las variables de entrada de un modelo. Se ejecuta el modelo múltiples veces, cada vez con diferentes valores aleatorios para las variables de entrada. Al final, se analizan los resultados de todas las simulaciones para obtener una distribución de probabilidad de los resultados. Esta técnica es muy útil para el análisis de riesgos y la toma de decisiones en condiciones de incertidumbre. En un contexto empresarial, se puede aplicar para realizar proyecciones financieras y evaluar el riesgo asociado con diferentes escenarios. Por ejemplo, una empresa de inversión podría usar la simulación de Monte Carlo para modelar el rendimiento de una cartera de inversiones en diferentes condiciones económicas, lo que les permitiría evaluar el riesgo y tomar decisiones informadas.
Simulación de sistemas dinámicos. Esta técnica se utiliza para modelar sistemas complejos y dinámicos. En lugar de analizar cada parte del sistema de forma aislada, esta técnica permite estudiar cómo interactúan todas las partes del sistema a lo largo del tiempo. Por lo general, se construyen modelos matemáticos complejos que describen cómo las variables del sistema evolucionan a lo largo del tiempo. Esta técnica es muy útil para entender cómo los sistemas complejos funcionan, predecir resultados futuros y probar diferentes escenarios. En un contexto empresarial, se puede aplicar para simular el comportamiento del mercado y predecir tendencias futuras. Por ejemplo, una empresa de marketing podría usar la simulación de sistemas dinámicos para modelar cómo los cambios en el comportamiento del consumidor podrían afectar la demanda de su producto en el futuro.
Simulación basada en agentes. Esta técnica se utiliza para modelar la interacción de múltiples agentes en un sistema. En esta técnica, se construyen modelos que describen cómo los agentes interactúan entre sí y con el entorno en el que operan. Los modelos pueden ser muy detallados y pueden incluir información sobre los comportamientos, preferencias y restricciones de los agentes. Esta técnica es muy útil para entender cómo los individuos o grupos interactúan en un sistema y cómo los cambios en las políticas o el entorno pueden afectar el comportamiento de los agentes. En un contexto empresarial, se puede aplicar para simular el comportamiento de los clientes y evaluar cómo sus decisiones individuales afectan el resultado final. Por ejemplo, una empresa de servicios financieros podría usar la simulación basada en agentes para modelar cómo los diferentes tipos de clientes toman decisiones de inversión y cómo esas decisiones afectan el rendimiento de una cartera de inversiones.
Simulación de juegos. Esta técnica se utiliza para modelar situaciones de toma de decisiones en un entorno competitivo. En esta técnica, se construyen modelos de juegos que describen cómo los jugadores interactúan entre sí y toman decisiones. Los modelos pueden ser muy complejos y pueden incluir información sobre las preferencias, restricciones y estrategias de los jugadores. Esta técnica es muy útil para analizar estrategias y resultados en situaciones competitivas. En un contexto empresarial, se puede aplicar para simular la competencia en un mercado y evaluar diferentes estrategias de negocio. Por ejemplo, una empresa de telecomunicaciones podría usar la simulación de juegos para modelar cómo diferentes estrategias de precios podrían afectar la participación de mercado y el margen de beneficio.
Simulación de eventos discretos. Esta técnica se utiliza para simular eventos que ocurren en momentos específicos y en orden secuencial. En esta técnica, se construyen modelos que describen cómo se producen los eventos y cómo se ven afectados por diferentes variables. Los modelos pueden ser muy detallados y pueden incluir información sobre los tiempos de llegada, los tiempos de servicio y las probabilidades de eventos específicos. Esta técnica es muy útil para analizar procesos de producción, logística, transporte y otros procesos que implican eventos discretos. En un contexto empresarial, se puede aplicar para simular el flujo de producción en una fábrica y evaluar la eficiencia del proceso. Por ejemplo, una empresa de fabricación podría usar la simulación de eventos discretos para modelar cómo diferentes configuraciones de la línea de producción podrían afectar la productividad y el tiempo de entrega.
Si bien es cierto que las técnicas de simulación expuestas pueden parecer similares, las situaciones en las que se utilizan son muy dispares.
6.3 Casos de uso
A continuación, se ofrecen algunos ejemplos de cómo se han utilizado las técnicas de simulación en diferentes áreas:
Industria: Las técnicas de simulación se utilizan comúnmente en la industria para optimizar el rendimiento de procesos complejos, como la producción de petróleo y gas, la fabricación de productos químicos, la producción de energía y la producción de alimentos. Por ejemplo, se pueden utilizar simulaciones para modelar el comportamiento de una planta de producción y determinar la mejor configuración de procesos y recursos para maximizar la producción y minimizar costes.
Logística: Las técnicas de simulación también se utilizan en la logística para modelar el movimiento de bienes y personas a través de una red de transporte. Por ejemplo, se pueden utilizar simulaciones para analizar el impacto de cambios en la infraestructura de transporte, como la construcción de una nueva carretera o la expansión de una red de ferrocarril, en el tiempo de viaje, la congestión del tráfico, etc.
Economía: Las técnicas de simulación se han utilizado durante mucho tiempo en la economía para modelar el comportamiento de los mercados y analizar el impacto de las políticas económicas. Por ejemplo, se pueden utilizar simulaciones para analizar cómo diferentes políticas fiscales y monetarias pueden afectar el crecimiento económico, la inflación y el desempleo.
Política: Las técnicas de simulación también se utilizan cada vez más en el análisis de políticas públicas para modelar el comportamiento de los sistemas complejos, como los sistemas de salud, los sistemas educativos y los sistemas de seguridad pública. Por ejemplo, se pueden utilizar simulaciones para modelar el impacto de diferentes políticas de atención médica en la accesibilidad, la calidad y el coste de la atención médica.
Estos son solo algunos ejemplos de cómo se han utilizado las técnicas de simulación en diferentes áreas. Cada vez más, las organizaciones están utilizando estas técnicas para analizar y predecir el comportamiento de sistemas complejos y mejorar la toma de decisiones.
6.4 El método de Monte Carlo
El método de Monte Carlo recibe su nombre de la ciudad de Monte Carlo en Mónaco, que es conocida por su famoso casino. Durante la década de 1940, los físicos Stanislaw Ulam y Nicholas Metropolis trabajaban en el proyecto Manhattan en Los Álamos, Nuevo México, y se encontraron con un problema que requería la generación de números aleatorios. Debido a su afición por los juegos de azar, Ulam sugirió utilizar la aleatoriedad presente en los juegos de azar para resolver el problema, haciendo una analogía con las probabilidades que se utilizan en los juegos de casino de Monte Carlo. Desde entonces, este método ha sido utilizado en una gran variedad de campos, como la física, la ingeniería, la biología, la economía y las finanzas, entre otros.

El método de Monte Carlo es una técnica de simulación estadística que se utiliza para estimar la distribución de probabilidad de un evento o variable aleatoria mediante la generación de múltiples muestras aleatorias. Como se ha expuesto anteriormente, este método se basa en la generación de un gran número de muestras aleatorias y en la utilización de técnicas estadísticas para analizar y resumir los resultados obtenidos. Este método se utiliza comúnmente para resolver problemas en los que la solución analítica es difícil o imposible de obtener. Por ejemplo, en física se utiliza para simular el comportamiento de sistemas complejos, como los fluidos, los plasmas y los sólidos, mientras que en finanzas se utiliza para simular el comportamiento de los precios de los activos financieros. En prospectiva, el método de Monte Carlo también se puede utilizar para simular el comportamiento de eventos futuros o variables aleatorias. Por ejemplo, se puede utilizar para simular el rendimiento de una cartera de inversión en el futuro, la demanda de un producto en el mercado o el riesgo de incumplimiento de un préstamo.
6.4.1 Bootstrap
El método Monte Carlo y el bootstrap son dos técnicas estadísticas que se utilizan para simular y analizar datos, pero tienen diferentes objetivos y aplicaciones.
El método Monte Carlo se utiliza para simular la distribución de probabilidad de una variable aleatoria mediante la generación de múltiples muestras aleatorias. Por ejemplo, se puede utilizar para simular el comportamiento de un sistema físico complejo o para estimar la distribución de rendimientos de una cartera de inversión. El método Monte Carlo se basa en la aleatoriedad y en la generación de muestras aleatorias para obtener estimaciones de la distribución de probabilidad de la variable de interés.
Por otro lado, el bootstrap es una técnica de remuestreo que se utiliza para estimar la distribución de probabilidad de una estadística de interés, como la media o la mediana, a partir de una única muestra de datos. En lugar de simular nuevas muestras aleatorias, el bootstrap utiliza la muestra original para generar múltiples muestras de datos simulados mediante un proceso de remuestreo con reemplazo. Estas muestras simuladas se utilizan para obtener estimaciones de la distribución de la estadística de interés, como la media o la mediana.
6.4.2 Teoría de colas
El método de Monte Carlo y la teoría de colas son dos técnicas estadísticas que se utilizan en conjunto para analizar y optimizar sistemas de colas o líneas de espera.
La teoría de colas se enfoca en el estudio del comportamiento de sistemas donde hay llegadas aleatorias de clientes o elementos a un sistema, como por ejemplo un centro de atención al cliente, una estación de servicio, un aeropuerto, etc. La teoría de colas utiliza modelos matemáticos para describir y analizar el comportamiento del sistema y los tiempos de espera de los clientes en la cola. A partir de estos modelos se pueden obtener medidas de desempeño, como la longitud media de la cola, el tiempo de espera promedio y la utilización del servidor.
Por otro lado, y como hemos comentado anteriormente, el método de Monte Carlo se utiliza para simular el comportamiento de un sistema a través de la generación de múltiples muestras aleatorias. El método de Monte Carlo se basa en la aleatoriedad y en la generación de muestras aleatorias para obtener estimaciones de la distribución de probabilidad de la variable de interés.
Cuando se utilizan en conjunto, el método de Monte Carlo y la teoría de colas permiten simular y analizar el comportamiento de un sistema de colas de manera precisa y eficiente. Por ejemplo, se pueden simular múltiples escenarios de llegada y servicio de clientes para evaluar diferentes políticas de atención al cliente y determinar cuál es la más adecuada en términos de tiempo de espera y utilización del servidor.
6.5 Ejemplos con R
Veamos ahora diferentes maneras de poner en práctica los conceptos anteriores. A continuación, se muestran varios ejemplos de cómo se puede utilizar R para realizar técnicas de simulación:
6.5.1 Ejemplo 1
Supongamos que queremos simular el lanzamiento de una moneda justa. En este caso, el resultado de cada lanzamiento será aleatorio y seguirá una distribución de probabilidad binomial con una probabilidad de éxito de 0.5. Para simular el lanzamiento de una moneda, puedes utilizar la función rbinom de R, que simula una variable aleatoria binomial:
En este caso, hemos simulado 1000 lanzamientos de una moneda, y los resultados se almacenan en el vector resultados_lanzamientos.
Una vez que tenemos los resultados de la simulación, se pueden calcular estadísticas sobre ellos, como la proporción de caras (1) y cruces (0) que aparecen:
# Calcular la proporción de caras y cruces
prop_caras <- sum(resultados_lanzamientos == 1) / n_lanzamientos
prop_cruces <- sum(resultados_lanzamientos == 0) / n_lanzamientos
# Imprimir los resultados
print(paste0("Proporción de caras: ", scales::number(prop_caras, accuracy = 0.0001)))[1] "Proporción de caras: 0.4950"print(paste0("Proporción de cruces: ", scales::number(prop_cruces, accuracy = 0.0001)))[1] "Proporción de cruces: 0.5050"Como se puede observar, la proporción de caras y cruces es aproximadamente 0.5, lo que es consistente con el hecho de que estamos simulando una moneda justa.
6.5.2 Ejemplo 2
Supongamos ahora que queremos simular el comportamiento del precio de una determinada acción a lo largo de un año. Partiremos del último precio conocido (el de hoy) y simularemos el precio del resto de días atendiendo a un modelo estadístico determinado.
# precio de la acción hoy
p <- 500
# creamos un vector vacío en el que guardaremos los precios generados
precios <- vector()
precios[1] <- p
# generamos el precio del día 2
mean <- 0
sd <- p/100
(precios[2] <- precios[1] + rnorm(n=1, mean=mean, sd=sd))[1] 498.339# simulamos los precios de todo el año
n_dias <- 365
for(t in 2:n_dias){
precios[t] <- precios[t-1] + rnorm(n=1, mean=mean, sd=sd)
}
ts.plot(precios)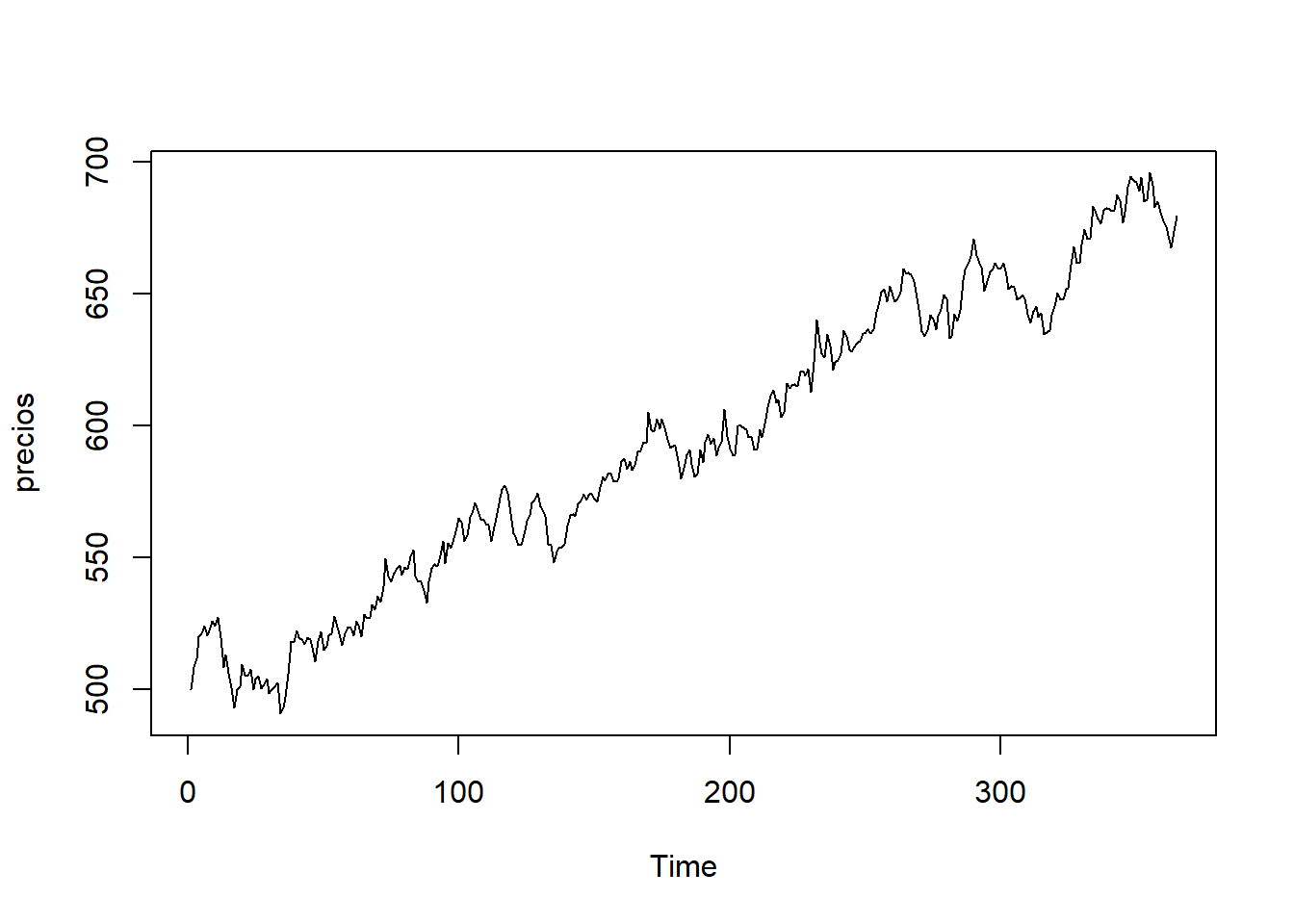
Cuando repetimos el proceso, puesto que nuestro modelo tiene un componente aleatorio, cada simulación ofrece un resultado distinto. Lo que ahora procede es crear una matriz en la que se incluyan las diferentes simulaciones realizadas:
n_sim <- 5
precios <- matrix(nrow = n_dias, ncol = n_sim)
precios[1,] <- p
head(precios) [,1] [,2] [,3] [,4] [,5]
[1,] 500 500 500 500 500
[2,] NA NA NA NA NA
[3,] NA NA NA NA NA
[4,] NA NA NA NA NA
[5,] NA NA NA NA NA
[6,] NA NA NA NA NAfor(s in 1:n_sim){
for(t in 2:n_dias){
precios[t,s] <- precios[t-1,s] + rnorm(n=1, mean=mean, sd=sd)
}
}
head(precios) [,1] [,2] [,3] [,4] [,5]
[1,] 500.0000 500.0000 500.0000 500.0000 500.0000
[2,] 498.8454 499.5958 503.1925 502.8256 498.4420
[3,] 496.7899 493.0991 499.3787 505.7109 506.5691
[4,] 502.0054 498.7059 503.3869 510.6031 511.1805
[5,] 502.7028 492.8524 502.2231 519.6080 518.1872
[6,] 493.5384 493.9765 500.1734 509.9761 519.0526ts.plot(precios) #col=1:ncol(precios)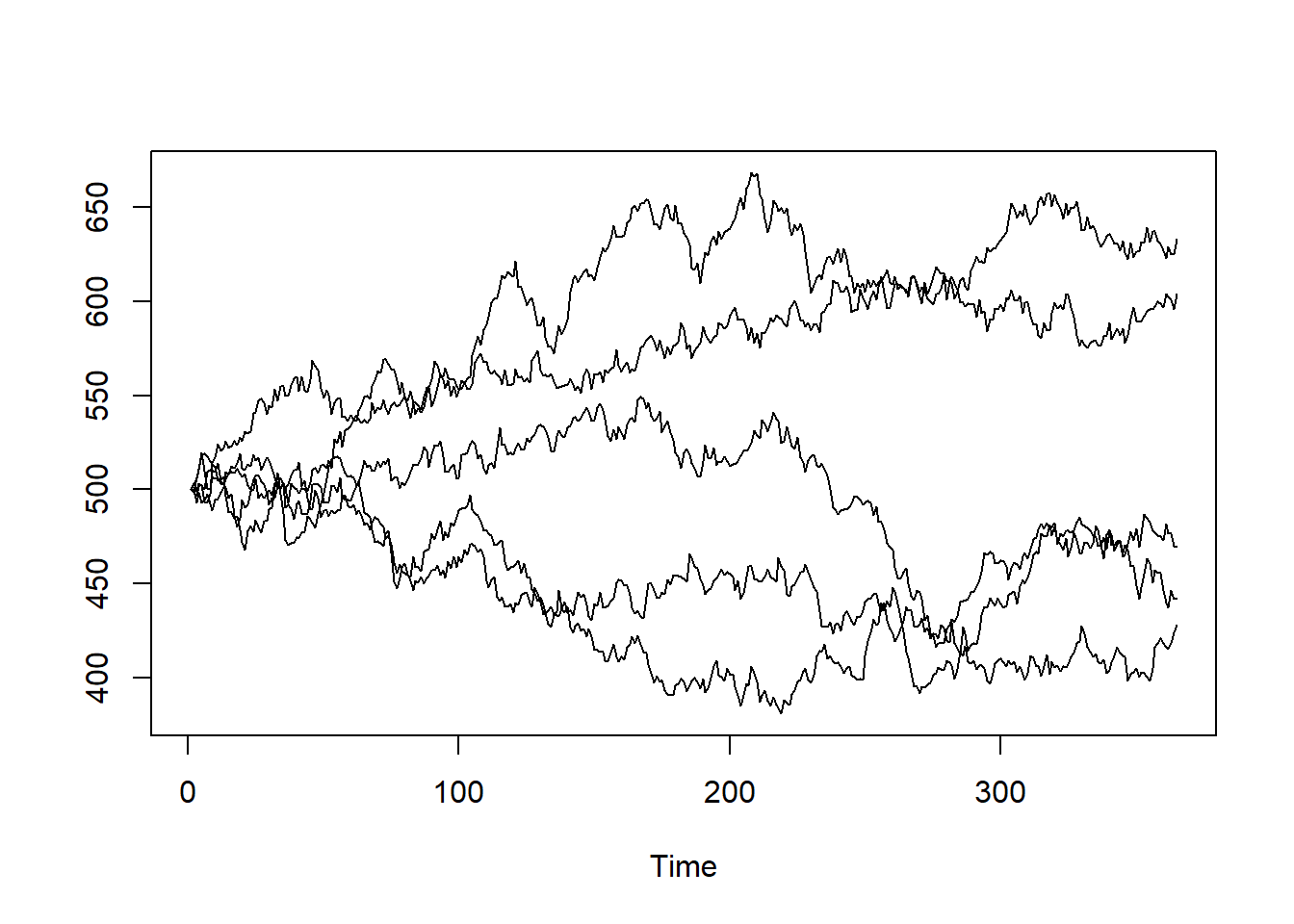
tail(precios) [,1] [,2] [,3] [,4] [,5]
[360,] 446.5301 626.9704 418.3722 472.9238 597.0272
[361,] 439.7609 622.8926 416.6027 481.8984 604.1922
[362,] 437.4672 629.0011 415.6229 476.6035 602.5349
[363,] 446.8080 625.0792 418.6471 476.9447 600.7908
[364,] 441.7280 624.9314 424.3335 470.2234 595.9585
[365,] 442.0588 632.9131 428.1903 469.4423 603.9641Si repetimos el proceso pero esta vez con 1000 simulaciones…
n_sim <- 1000
precios <- matrix(nrow = n_dias, ncol = n_sim)
precios[1,] <- p
for(s in 1:n_sim){
for(t in 2:n_dias){
precios[t,s] <- precios[t-1,s] + rnorm(n=1, mean=mean, sd=sd)
}
}
ts.plot(precios)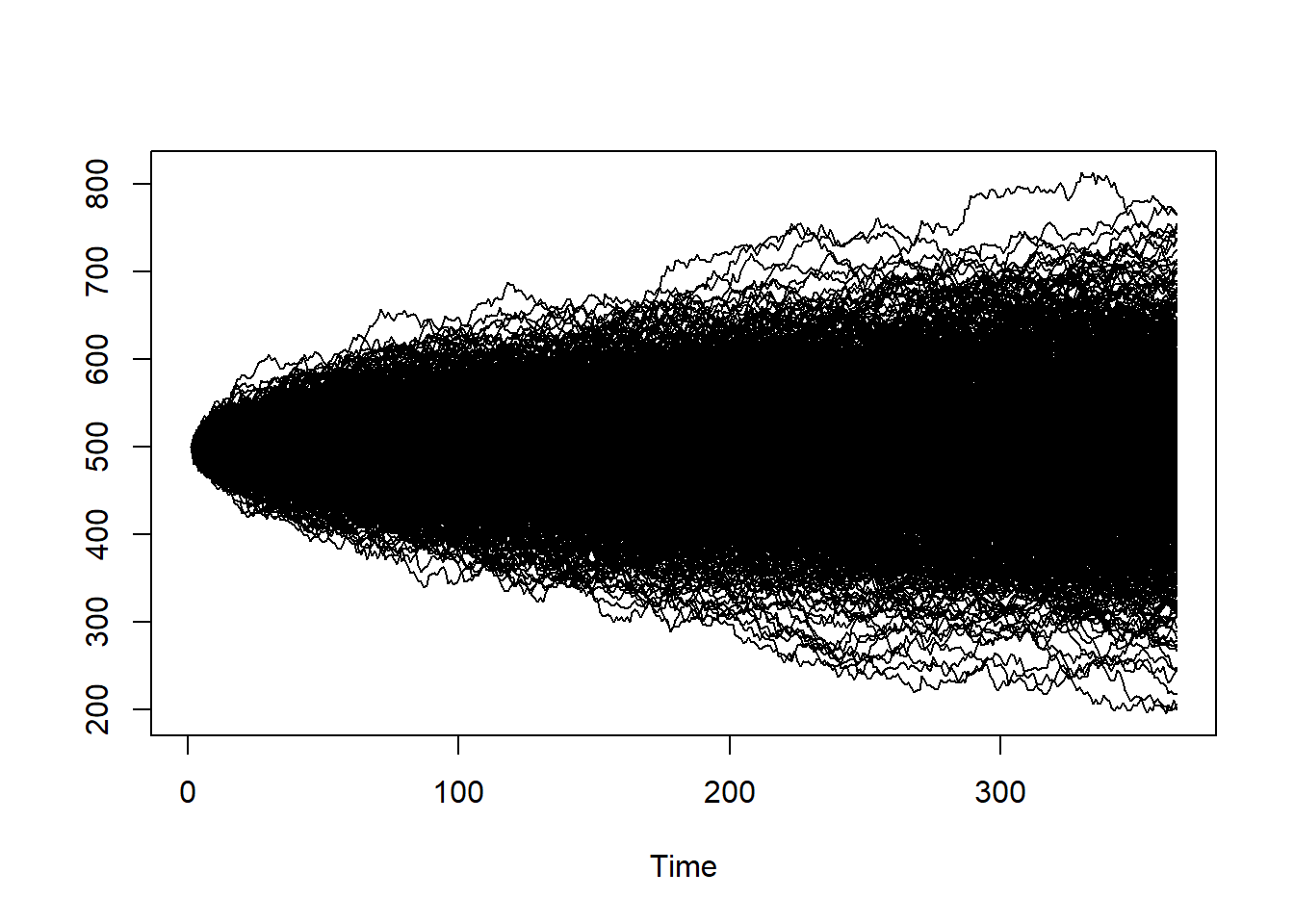
precios_finales <- precios[n_dias,]
hist(precios_finales)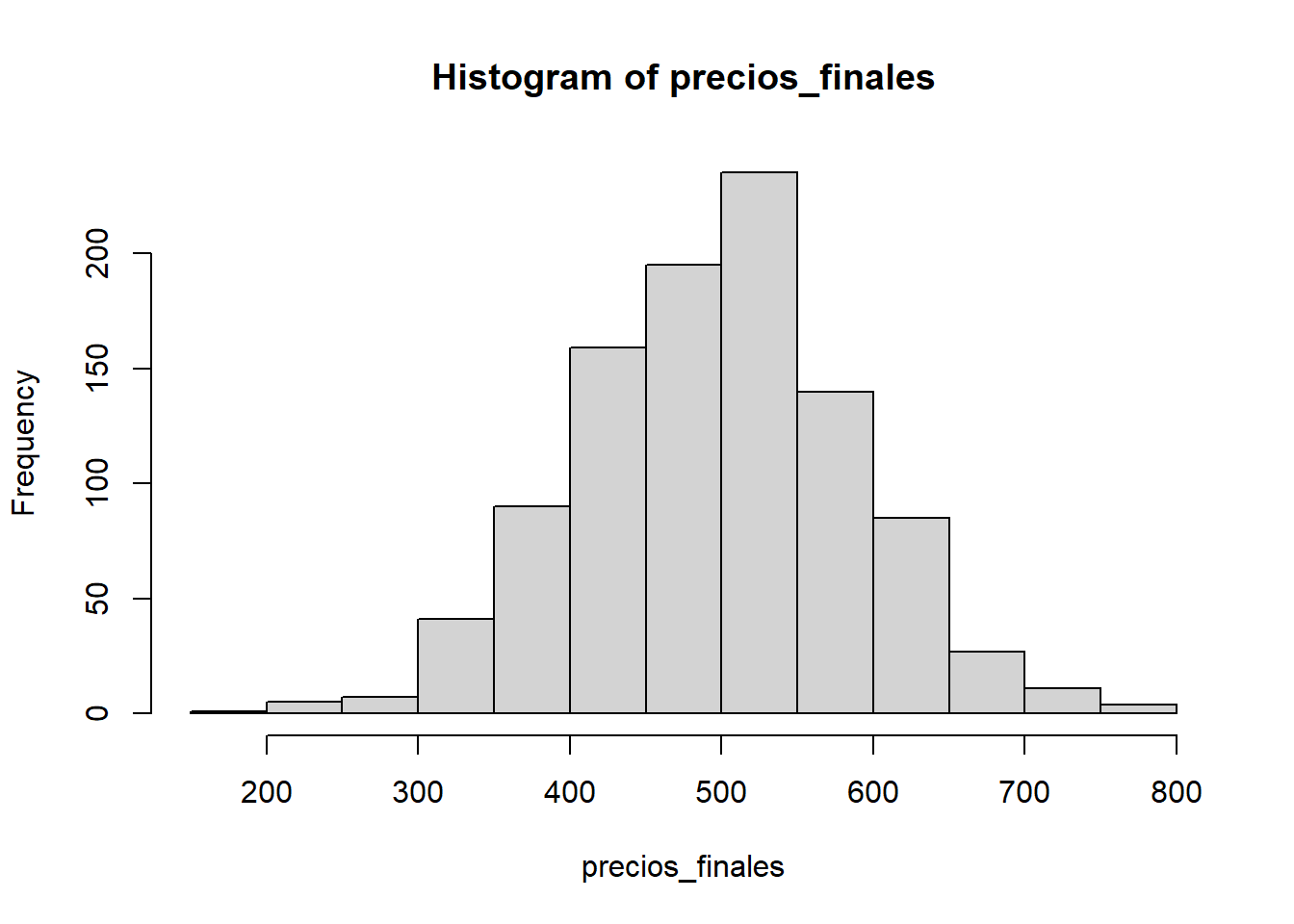
summary(precios_finales) Min. 1st Qu. Median Mean 3rd Qu. Max.
199.5 432.7 500.2 496.7 554.1 766.8 # intervalo de confianza
mean(precios_finales) + c(-1,1)*qnorm(.975)*sd(precios_finales)[1] 318.3636 674.9403# ordenamos los precios finales de mayor a menor
precios_finales <- precios_finales[order(precios_finales, decreasing = T)]
head(precios_finales)[1] 766.8487 765.3661 754.8141 752.1761 745.2194 739.0774tail(precios_finales)[1] 248.3706 245.3487 244.5496 217.4478 207.0099 199.5167# precio que deja un 5% por debajo
precios_finales[.95*n_sim][1] 348.68186.5.3 Ejemplo 3
Supongamos que eres gerente de un pequeño negocio en el que vendes un determinado producto a un precio fijo, por ejemplo 50 euros. Quieres saber cuánto dinero esperas ganar en un día típico de ventas. Sin embargo, debido a la naturaleza estocástica de las ventas, no puedes predecir con certeza cuánto dinero ganarás.
Para simular tus ventas diarias, se pueden seguir los siguientes pasos. En primer lugar, definimos una función que simule las ventas de un día. Esta función debe tomar como entrada el número de clientes que entran en la tienda ese día, y devolver la cantidad de dinero que se obtiene por ventas ese día. Para simplificar, supongamos que el número de clientes sigue una distribución normal con media 30 y desviación estándar 5, y que la cantidad de dinero que se obtiene por venta sigue una distribución normal con media 50 y desviación estándar 10. La función podría verse así:
ventas_diarias <- function(num_clientes) {
ventas <- rnorm(num_clientes, mean = 50, sd = 10)
return(sum(ventas))
}Ahora simulamos un gran número de días de ventas (por ejemplo, 1000 días), y para cada día, simulamos el número de clientes que entran en la tienda. Para simplificar, supongamos que el número de clientes sigue una distribución normal con media 30 y desviación estándar 5:
num_dias <- 1000
clientes_por_dia <- rnorm(num_dias, mean = 30, sd = 5)Para cada día, usamos la función ventas_diarias para simular las ventas y guardar los resultados en un vector. Podemos hacer esto con un bucle for, como en el ejemplo anterior, o con la función sapply():
resultados <- sapply(clientes_por_dia, ventas_diarias)Ahora calculamos la ganancia media diaria, la desviación estándar de la ganancia diaria y un intervalo de confianza del 95% para la ganancia diaria:
ganancia_media <- mean(resultados)
ganancia_sd <- sd(resultados)
ganancia_ci <- t.test(resultados)$conf.intCon estos pasos, hemos simulado mediante el método de Monte Carlo (generando números aleatorios) las ventas diarias del negocio de una forma trivial. Incluyamos ahora más variables que influyen (pueden influir) en la probabilidad de éxito en la venta. En el siguiente ejemplo, la variable tamanio_empresa es un vector que contiene los posibles tamaños de empresa (“Pequeña”, “Mediana”, “Grande”). Se utiliza la función sample() para seleccionar de forma aleatoria un valor del vector en cada simulación, y se ajustan las ganancias según el tamaño de la empresa con una estructura condicional if-else.
# Definición de variables
precio_base <- 1000 # precio promedio al que se vende un producto o servicio
prob_exito <- 0.5 # probabilidad de que la venta ocurra
coste_total <- 500 # coste promedio de producir/vender el producto o servicio
tamanio_empresa <- c("Pequeña", "Mediana", "Grande")
# Función para calcular ganancias
calcular_ganancias <- function(precio_base, prob_exito, coste_total, tamanio_empresa) {
# Generación de variables aleatorias
precio_venta <- rnorm(1, mean = precio_base, sd = 100)
exito <- rbinom(1, size = 1, prob = prob_exito)
coste_venta <- rnorm(1, mean = coste_total, sd = 50)
tam_empresa <- sample(tamanio_empresa, 1, replace = TRUE)
# Cálculo de ganancias
if (exito == 1) {
ganancias <- precio_venta - coste_venta
} else {
ganancias <- 0
}
# Ajuste de ganancias según tamaño de la empresa
if (tam_empresa == "Pequeña") {
ganancias <- ganancias * 0.8
} else if (tam_empresa == "Mediana") {
ganancias <- ganancias * 0.9
} else {
ganancias <- ganancias * 1.1
}
return(ganancias)
}
# Simulación
set.seed(123)
num_simulaciones <- 10000
resultados <- rep(0, num_simulaciones)
for (i in 1:num_simulaciones) {
resultados[i] <- calcular_ganancias(precio_base, prob_exito, coste_total, tamanio_empresa)
}
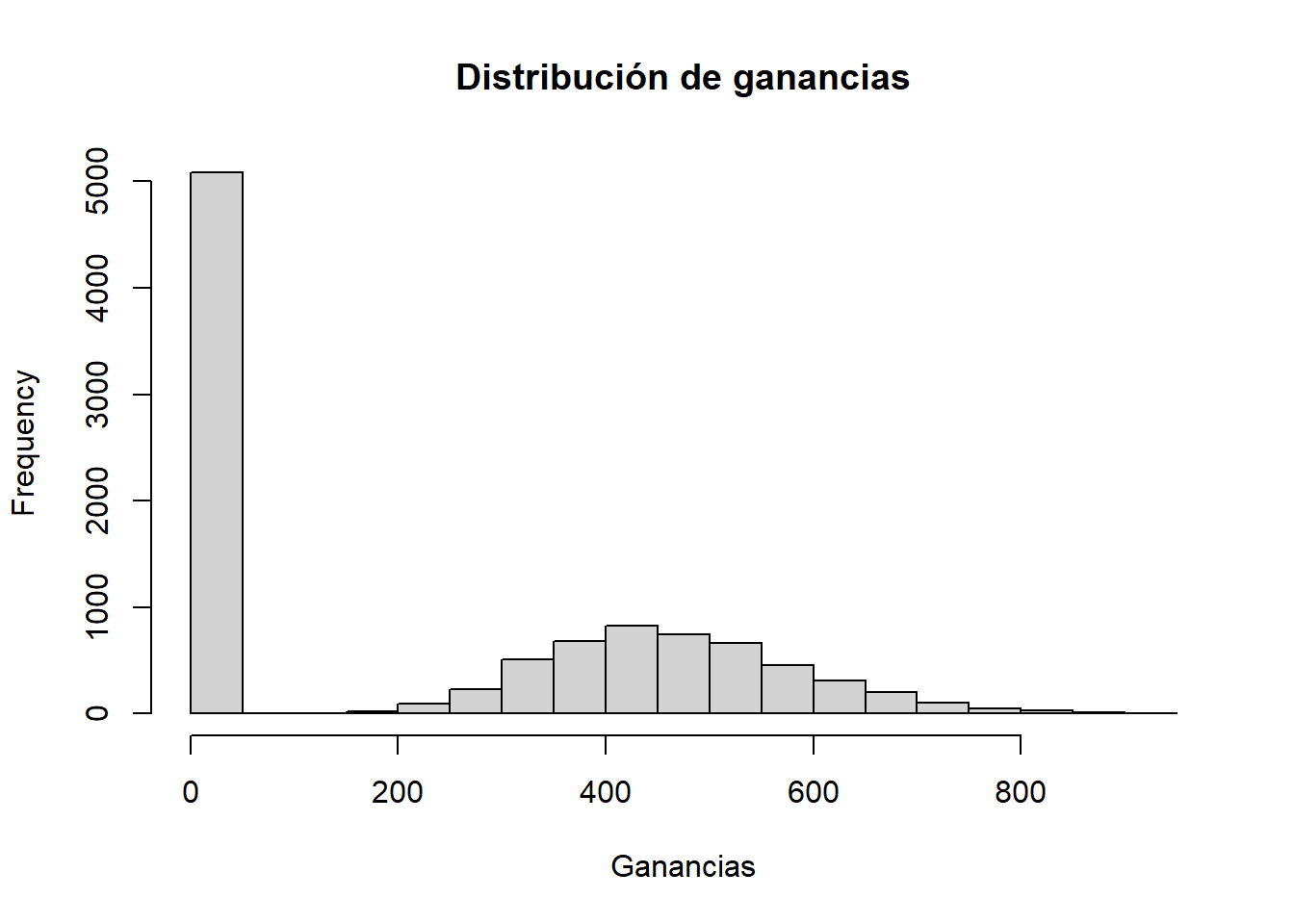
# Análisis de resultados
mean_resultados <- mean(resultados)
cat("Las ganancias esperadas son:", round(mean_resultados, 2))Las ganancias esperadas son: 229.21hist(resultados, breaks = 20, main = "Distribución de ganancias", xlab = "Ganancias")