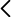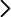Targetes i suports per a targetes

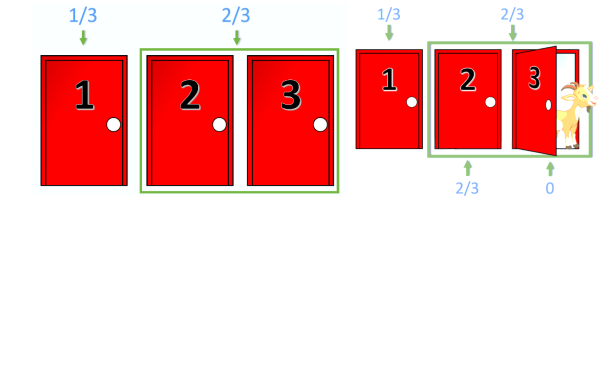
El problema de Monty Hall és un famós dilema matemàtic de probabilitat que es basa en un escenari hipotètic inspirat en el concurs televisiu nord-americà Let's Make a Deal. La situació és la següent: Imagina que ets en un concurs i has de triar entre tres portes tancades. Darrere d'una hi ha un cotxe i darrere de les altres dues, hi ha sengles cabres (com a exemple de premi sense valor). Esculls una porta, per exemple, la número 1. El presentador, que sap el que hi ha darrere de cada porta, obre una altra porta, diguem-ne la número 3, revelant sempre una cabra (és a dir, l'única porta amb cabra si la que has fet elegit amaga una cabra o una aleatòria entre les dues possibilitats que hi hauria si has triat la porta del cotxe). Després us ofereix l'oportunitat de canviar la vostra elecció inicial per l'altra porta tancada, la número 2. La pregunta és: Hauries de mantenir la teva elecció original o canviar a l'altra porta? Augmenten les teves probabilitats de guanyar el cotxe si canvies de porta? La resposta (per a alguns) contraintuïtiva és que sí que hauries de canviar de porta. Al principi, la probabilitat que el cotxe estigui darrere de la porta que vas triar és de 1/3, i la probabilitat que estigui darrere d'una de les altres dues portes és de 2/3. Quan el presentador obre una porta que té una cabra, la probabilitat de 2/3 no canvia, però ara es concentra a l'única porta que queda tancada. Per tant, canviar de porta duplica les teves possibilitats de guanyar el cotxe a 2/3. Aquest problema ha generat molt de debat i confusió perquè desafia la intuïció de moltes persones, però matemàticament canviar de porta és l'estratègia que maximitza les teves possibilitats de guanyar [1]. En aquesta demostració es proposa fer l'experiment repetides vegades per mostrar quina és la millor estratègia acumulant prou estadística. Hi ha també llocs web on es pot fer aquesta simulació [2]. Molta gent raona que tant és canviar o no, ja que la probabilitat d'encertar és del 50% en cadascuna, però això només seria cert per al cas en què el jugador triés després d'obrir una de les portes.

Per poder fer moltes proves in situ, s'utilitzen tres targetes plastificades que es poden col·locar sobre suports (els numerats de l'1 al 3). A cada targeta hi ha una porta per una banda i un cotxe o una cabra per l'altra. Hi ha més targetes amb cabres per a una prova que s'explicarà després. El procediment és el següent:

1) S'escull un “secretari” que sortirà a la pissarra per apuntar quins van sent els resultats (és a dir, si cada estudiant-concursant s'emporta el cotxe o no) 2) Es pregunta als alumnes si es quedarien amb la porta inicial , si canviarien o si pensen que és igual. Es fan així dos grups, un amb els que canviarien i un altre amb els que no canviarien o pensen que és igual. Alternativament es poden incloure els que pensen que tant és a l'altre grup si així s'aconsegueixen grups més parells en nombre. Aquesta classificació es fa prèviament per evitar que conforme vegin el que trien els companys anteriors o el resultat de les proves, acabin tots escollint el mateix. 3) Es duu a terme el concurs amb cadascun dels estudiants (primer per a un dels grups anteriors, després per a l'altre, per facilitar el comptatge per part del secretari). A cada prova el professor estudia les cartes, col·locant-les en el suport de manera que mostrin als alumnes les portes. L'alumne tria una porta, el professor “obre” una de les altres dues que no té cabra i l'alumne canvia la seva elecció o no segons hagi triat estar al grup dels que canvien o no. El secretari apunta si encerta o no amb la seva “elecció” final. 4) Per assegurar que hi ha prou estadística, es poden fer diverses rondes per a cadascun dels grups, de manera que al final es tinguin uns 30 casos almenys en ambdós grups, millor si són 40. Una manera perquè els alumnes vegin de manera més intuïtiva que el millor és canviar és plantejar l'experiment amb 10 portes, només amb un premi. En aquest cas és més evident que si triem una porta a l'atzar i el presentador obre 8 portes sense premi, el més raonable és canviar de porta perquè clarament la probabilitat d'haver encertat a la nostra primera elecció és molt baixa (10%). Aquesta prova es pot realitzar amb els suports i targetes addicionals (hi ha també una targeta extra de reemplaçament).

Es pot comentar que és un problema que s'esmenta en diversos elements de cultura popular, per exemple: El problema va ser popularitzat per Marilyn vos Savant a la seva columna de la revista Parade Magazine el 1990, fet que va portar a un ampli debat públic sobre la solució correcta. Aquesta història s'esmenta a la novel·la “El curiós incident del gos a mitjanit”, de M. Haddon. També apareix a la pel·lícula “21 blackjack”, dirigida per R. Luketic, o en episodis de les sèries Friends, Broklyn Nine-Nine o The Hollow

[1] https://es.wikipedia.org/wiki/Problema_de_Monty_Hall [2] https://www.mathwarehouse.com/monty-hall-simulation-online/