Transparencias con redes periódicas de puntos. Círculos de Ewald de distintos tamaños. Pasador de papel para sujetar los círculos. Rotulador de transparencias.
ES NECESARIO PROYECTOR.
- Elegir la red periódica bidimensional que se desee utilizar.
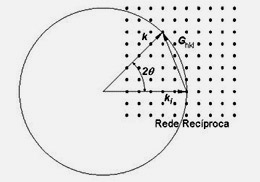
- Elegir el círculo de Ewald con el que se desee ilustrar la difracción. El vector k de la radiación incidente está pintado en el círculo.
- Introducir el pasador para sujetar el círculo de Ewald por uno de sus extremos sobre uno de los puntos de red perforados.
- Girar el círculo hasta que uno de los puntos de red toque el borde del círculo (“superficie de la esfera de Ewald”). Esto es equivalente a cambiar el ángulo de incidencia de los rayos X. El vector que va del centro del círculo al punto de red en su superficie indica la dirección de difracción. El vector que une los dos puntos de red es el vector de la red recíproca es el que aparece en la condición de Bragg.
- Girar la red. Esto es equivalente a girar el cristal. Obviamente, el efecto global es el mismo que en el punto 4, pero ahora la dirección de la radiación incidente se mantiene fija en el espacio.
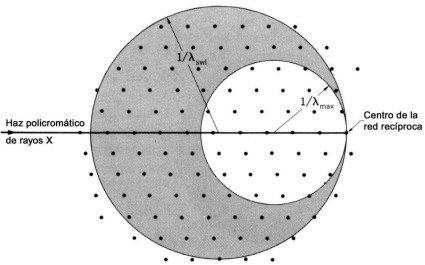
- Utilizar un círculo de distinto tamaño y sujetarlo al mismo punto de red, de forma que sus dos radios coincidan. Los puntos comprendidos entre el círculo pequeño y el grande satisfarán la condición de difracción si se hace un barrido en frecuencia.
Fundamento teórico:
La esfera de Ewald es una construcción que permite determinar las direcciones en las que se cumple la condición de difracción conociendo la red recíproca de un cristal y las características de la radiación incidente. En este modelo bidimensional la esfera está representada por un círculo.
Sea k el vector de ondas de la radiación incidente, la esfera de Ewald es una esfera de radio k que se dibuja sobre la red recíproca. El origen de la red recíproca, que tomamos en un punto arbitrario, se encuentra situado en la superficie de la esfera.
La condición de difracción de Laue establece que la diferencia entre el vector de ondas del rayo difractado, k’, y el incidente k, deben coincidir con un vector de la red recíproca, G:
La construcción de Ewald garantiza que se cumple la condición de difracción para aquellos puntos de la red recíproca que se encuentran en su superficie. La dirección de difracción viene dada por el vector k’, vector que tiene su origen en el centro de la esfera y termina en un punto de red contenido en la superficie de la esfera. El ángulo que forman los vectores k y k’ es dos veces el ángulo de difracción (2), tal como aparece en la figura 1.