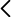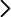Manómetro con tubo en forma de U y líquido coloreado, pera de goma

Descripción

El manómetro consta de un tubo en forma de U (dos ramas verticales y paralelas conectadas en U por el extremo inferior, tal y como se muestran en la Figura 1). Al introducirse un líquido coloreado en el tubo, su nivel en ambas ramas es el mismo (figura 2a). Si por uno de los extremos ejercemos una presión con la goma de pera (figura 2 b), veremos que el nivel en cada una de las ramas es distinto. Podemos observar que a mayor presión ejercida el desnivel es mayor, y que el líquido en una determinada rama puede ascender o descender dependiendo si disminuimos o aumentamos la presión ejercida en la rama.

Explicación - Fundamento teórico

La ecuación de Bernoulli nos proporciona una relación entre las variaciones de presión en un fluido y la velocidad y cambios de altura que experimenta el fluido en su recorrido. Esta puede deducirse fácilmente a partir de la conservación de la energía mecánica, asumiendo que esta no se disipa debido al rozamiento (asumimos un fluido ideal no viscoso) y que el fluido es incompresible (su densidad permanece constante). Bajo estas condiciones, la suma de los términos P (presión manométrica), ½ρv² (presión cinética) y ρgh (presión hidrostática) permanece constante a lo largo de la línea de corriente del fluido:

        P + ½ρv² + ρgh = cte                                                                         (1)

A partir de la ecuación (1), resulta sencillo deducir que si el fluido se encuentra en reposo (v=0), entonces la diferencia de presión entre dos puntos del fluido situados a distinta altura o profundidad vendrá dada por:           P₂-P₁ = ρgh                                                                                      (2)

siendo h en este caso la distancia entre los dos puntos (h1-h2). La ecuación (2) se conoce como ecuación fundamental de la hidrostática, y también puede deducirse teniendo en cuenta que la diferencia de presión entre dos puntos de un fluido en reposo es debida al peso de la columna de fluido delimitado por esos dos puntos:

Peso columna = m·g = ρVg Presión = Peso/S = ρgh

La ecuación fundamental de la hidrostática puede obtenerse también considerando el balance de fuerzas sobre un elemento de fluido (en reposo) de altura dz (tal y como se ilustra en la figura), de forma que debe cumplirse que la fuerza neta sea cero (equilibrio).

F₂-F₁-Peso = 0 (P+dP)·S-P·S-ρ·g·S·dz = 0  dP = ρgdz

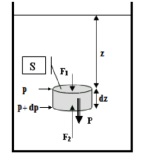 Cuya integración entre dos niveles 1 y 2 (considerando la densidad constante) da como resultado la ecuación 2.

 La consecuencia más importante de la ecuación (2) para esta demo es que a partir de la medida de la diferencia de alturas (h) es posible obtener el valor de la diferencia de presión entre los dos puntos   (∆P).

 Generalmente, uno de los niveles es la presión atmosférica (referencia), y la ecuación (2) quedaría como:

        ∆P= ρgh → P = Patm + ρgh                                                               (3)

En el caso, por ejemplo, de un fluido como el agua, la ecuación (3) indica que la presión P aumenta con la profundidad h (de hecho, en el caso del agua aproximadamente 1 atm cada 10 m). Hay que tener en cuenta que en aquellos casos en los que un aumento de h implique una disminución de la presión, el signo + deberá sustituirse por un signo negativo. Este suele ser el caso del ascenso por una montaña, en la que al aumentar la altura sobre el nivel del mar disminuye la presión. Sin embargo, en este caso la ecuación (3) no podría ser aplicada porque la densidad del aire no es constante con la altura.

Ejemplo de medida de la presión (manómetro)

La Figura 2 detalla cómo, midiendo el desnivel h se puede determinar la diferencia de presión ∆P y la presión P (ec. 3). En el tubo se ha introducido agua con un colorante para poder visualizarla. Inicialmente, las presiones sobre ambas ramas son iguales y por lo tanto el líquido se encuentra al mismo nivel (Figura 2a). Al aspirar con la pera de goma colocada en la rama izquierda, se produce una disminución de presión y la altura del líquido en esta rama aumenta y en la de la derecha disminuye (Figura 2b). La lectura sobre la regla graduada proporciona el valor de presión que hemos ejercido con la pera de goma (Figura 2c). Hay que tener en cuenta que la regla que incorpora el instrumento ya está calibrada en presiones (en concreto en kPa), y podemos obtener el valor de ∆P directamente de la lectura de la escala (línea verde en la Figura 2c). También se puede realizar la medida de la longitud entre el nivel superior e inferior del líquido con una regla y realizar el cálculo (línea roja en la Figura 2c). En este caso, la separación entre los dos niveles de líquido es de 9.4 cm, por lo que, según (3):

∆P = ρgh = 1000·9.8·0.094 = 921.2 Pa = 0.92 kPa (aprox. 0.0091 atm)

Para calcular la presión total ejercida (3): P = Patm + ρgh = 101.33+ 0.92 kPa =102,25 kPa

Figura 2. (a) Manómetro con tubo en forma de U utilizando agua con colorante como líquido. Si no se ejerce ningún tipo de presión, el nivel de líquido en ambas ramas es el mismo.

(b) Pera de goma utilizada para “aspirar” por la rama izquierda, de forma que el líquido se desnivela debido a la diferencia de presión.

(c) Valor de la presión sobre la escala graduada del instrumento (en kPa) o bien realizando la medida de la distancia entre los dos puntos del líquido.

- Se pueden medir distintos términos de presión: globos de distinto radio, aspirar como si fuera una pajita, etc. En este caso, por motivos de higiene conviene desinfectar la rama tras su uso.

- Se puede utilizar como fluido agua y un alcohol para ver el efecto de la densidad del fluido sobre la medida de la presión.

-Las presiones que pueden medirse con este instrumento son muy bajas, por lo que hay que tener cuidado ya que el líquido puede salirse fácilmente del tubo al presionar la pera.

-Conviene llevarse a clase el instrumento con el líquido ya incluido.

Se puede visualizar una versión de este experimento en la siguiente clase del profesor Walter Lewin, entre los minutos 42:00 – 45:20 https://www.youtube.com/watch?v=O_HQklhIlwQ