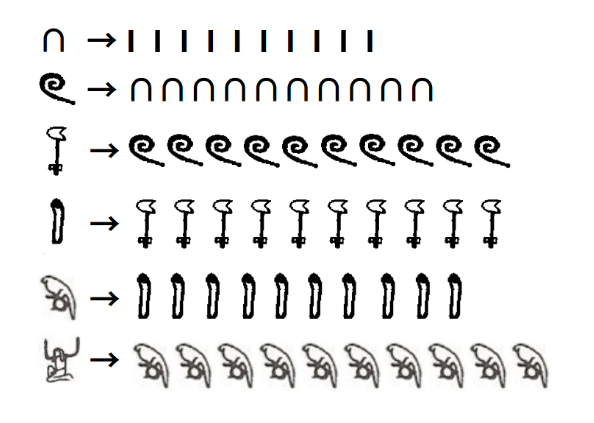
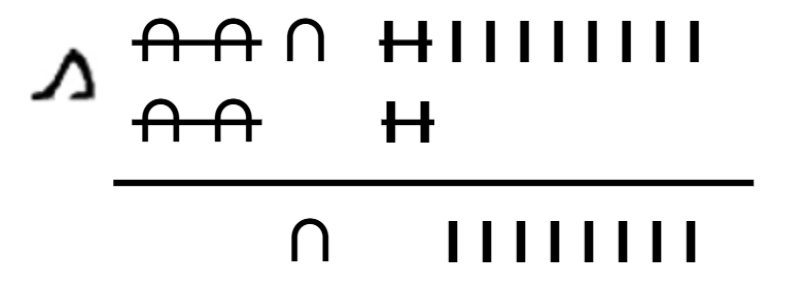En el cas d’haver de realitzar una resta portada com la coneixem actualment, els egipcis realitzaven un canvi d’unitats paregut al nostre, pero en compte d’anomenar-lo prèstec li denominaren conversió o reconversió. Així, un símbol de numeració major es transforma en 10 símbols de la unitat menor. D’aquesta manera, la conversió de símbols és:
Per tant si volem operar 40 - 22, hauriem de seguir els següents passos:
1. Descomposar els dos nombres i escriure en sistema decimal de numeració en base 10:
40 = 4x10 + 0x1 → ∩ ∩ ∩ ∩
22 = 2x10 + 2x1 → ∩ ∩ I I
2. Col·locar els nombres en ordre agrupant els símbols iguals.
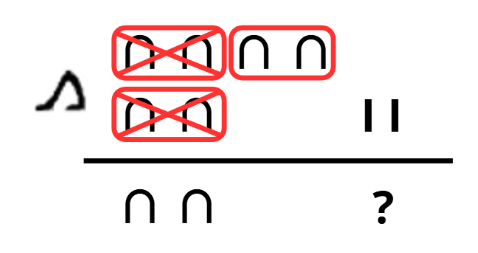
Com podem veure, podem operar amb el símbol ∩, ja que tenim una quantitat major al minuend que al subtrahend. No obstant això, en el cas del símbol I tenim una quantitat major al subtrahend que al minuend, per tant, no podem operar-les. El nombre 40 és igual a ∩ ∩ ∩ ∩ per tant, com no tenim símbols I; hi ha que fer una conversió ∩ → I.
∩ = I I I I I I I I I I
D’aquesta manera, tindriem:
Al minuend → 3x10 + 10x1 (∩∩∩ I I I I I I I I I I)
Al subtrahend → 2x10 + 2x1 (∩∩ I I)
Realitzem la resta: