7  Librería sf

7.1 Simple Features

El paquete sf(Pebesma, 2018, 2022), abreviatura de Simple Features, es una herramienta moderna y poderosa en el lenguaje de programación R diseñada específicamente para el manejo y análisis de datos geoespaciales. Este paquete proporciona un enfoque simple y coherente para trabajar con datos espaciales, permitiendo a los usuarios de R manipular, visualizar y analizar datos espaciales de manera eficiente y efectiva.

Desarrollado para reemplazar y ampliar las capacidades de paquetes más antiguos como sp(Pebesma y Bivand, 2023) y rgdal(Bivand et al., 2017), sf ofrece una integración completa con el sistema de objetos de R y trabaja de manera armoniosa con paquetes populares en el ecosistema de R como dplyr(Wickham, François, et al., 2023), tidyr(Wickham, Vaughan, et al., 2023) y ggplot2(Wickham, 2016). Esto facilita la realización de tareas comunes de manipulación de datos, como la selección, filtración y agregación, directamente en conjuntos de datos espaciales.

El paquete sf soporta múltiples tipos de geometrías espaciales, incluyendo puntos, líneas, polígonos y sus variantes combinadas, lo que lo hace adecuado para una amplia gama de aplicaciones geoespaciales. La estructura de datos de sf está alineada con el estándar Simple Features de la Open Geospatial Consortium, lo que garantiza la compatibilidad con una amplia variedad de herramientas y formatos de datos espaciales.

Las capacidades clave de sf incluyen:

  • Lectura y escritura eficiente: sf puede leer y escribir una variedad de formatos de archivo geoespacial comunes, incluyendo Shapefile, GeoJSON, KML y muchos otros, a través de la integración con la biblioteca GDAL.

  • Manipulación de datos espaciales: Permite realizar operaciones espaciales como el cálculo de distancias, áreas, intersecciones, uniones y otros tipos de análisis geométrico.

  • Visualización de datos espaciales: Integración con ggplot2 para la creación de visualizaciones de datos espaciales avanzadas y de alta calidad.

  • Análisis espacial: Facilita la realización de análisis espacial, incluyendo la medición de autocorrelación espacial o la creación de modelos de regresión espacial, entre otros.

7.2 Instalación del paquete sf

Del mismo modo que hacemos con otros paquetes, para poder utilizarlo hay que instalarlo y cargarlo.

install.packages("sf")
library(sf)
Linking to GEOS 3.12.2, GDAL 3.9.3, PROJ 9.4.1; sf_use_s2() is TRUE
Advertencia

Cuando cargamos la librería, nos aparece un mensaje informativo. Hablaremos de esto más adelante pero, ¿a qué crees que hace referencia?

Recordemos una forma de comprobar qué versión del paquete tenemos instalada:

packageVersion("sf")
[1] '1.0.19'

7.3 Cómo crear un objeto sf

Los objetos sf se forman como integración de unas piezas o subclases que heredan las características de la norma UNE ISO19125. Básicamente un objeto sf se descompone en dos objetos: uno de tipo sfc (simple feature column) y otro de tipo data.frame. A su vez, un objeto sfc se origina a partir de un objeto sfg (simple feature geometry), pudiéndole añadir un CRS (sistema de coordenadas de referencia). Los objetos sfg pueden ser de tipo POINT, LINESTRING, etc. Veamos más detenidamente cada tipo de objeto, comenzando por los más básicos hasta llegar a sf.

7.3.1 sfg

La clase sfg almacena la geometría con la información gráfica del objeto: las coordenadas, dimensiones, tipo de geometría… Hay 17 tipos posibles, pero los 7 más utilizados son:
- POINT: un punto simple (un vector x,y).
- MULTIPOINT: múltiples puntos (una matriz cada fila un punto).
- LINESTRING: secuencia de 2 o mas puntos conectados por lineas rectas.
- MULTILINESTRING: múltiples lineas (lista de matrices).
- POLYGON: un polígono cerrado (lista de matrices).
- MULTIPOLYGON: múltiples polígonos.
- GEOMETRYCOLLECTION: cualquier combinación de los anteriores.

Para crear cualquiera de estas geometrías básicas la librería sf contiene una serie de funciones creadoras: st_point(), st_multipoint(), st_linestring(), st_polygon(). Veamos algunos ejemplos.

7.3.1.1 Point

sf::st_point(c(5, 2))                 # XY point
POINT (5 2)
sf::st_point(c(5, 2, 3))              # XYZ point
POINT Z (5 2 3)
sf::st_point(c(5, 2, 1), dim = "XYM") # XYM point
POINT M (5 2 1)
sf::st_point(c(5, 2, 3, 1))           # XYZM point
POINT ZM (5 2 3 1)

Los resultados muestran que los tipos de puntos XY (coordenadas 2D), XYZ (coordenadas 3D) y XYZM (3D con una variable adicional, normalmente precisión de medición) se crean a partir de vectores de longitud 2, 3 y 4, respectivamente. El tipo XYM debe especificarse utilizando el argumento dim (que es la abreviatura de dimensión).

7.3.1.2 Multipoint

Para generar objetos tipo multipoint o linestring, trabajaremos con matrices, en lugar de con vectores. La función rbind() facilita esta tarea.

punto1 <- sf::st_point(c(5,2))
punto2 <- sf::st_point(c(4,3))
punto1
POINT (5 2)
class(punto1)
[1] "XY"    "POINT" "sfg"  
plot(punto1, axes = T, xlab = "X", ylab = "Y", pch=19)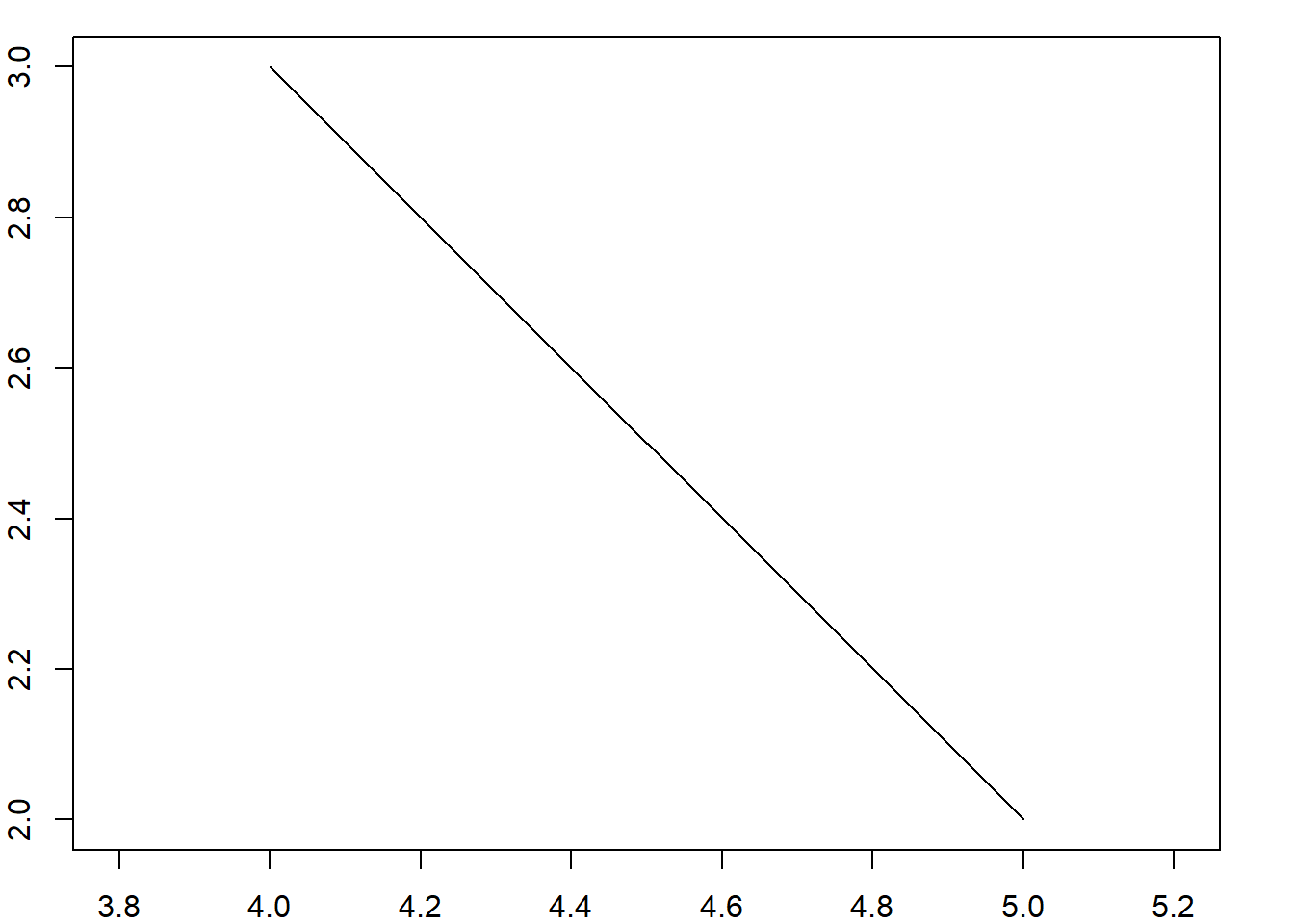

matriz_puntos <- rbind(punto1,punto2)
matriz_puntos
       [,1] [,2]
punto1    5    2
punto2    4    3
class(matriz_puntos)
[1] "matrix" "array" 
multipunto <- sf::st_multipoint(matriz_puntos)
multipunto
MULTIPOINT ((5 2), (4 3))
class(multipunto)
[1] "XY"         "MULTIPOINT" "sfg"       
par(mar = c(2,2,1,2))
plot(multipunto, axes = T, xlab = "X", ylab = "Y", pch=19)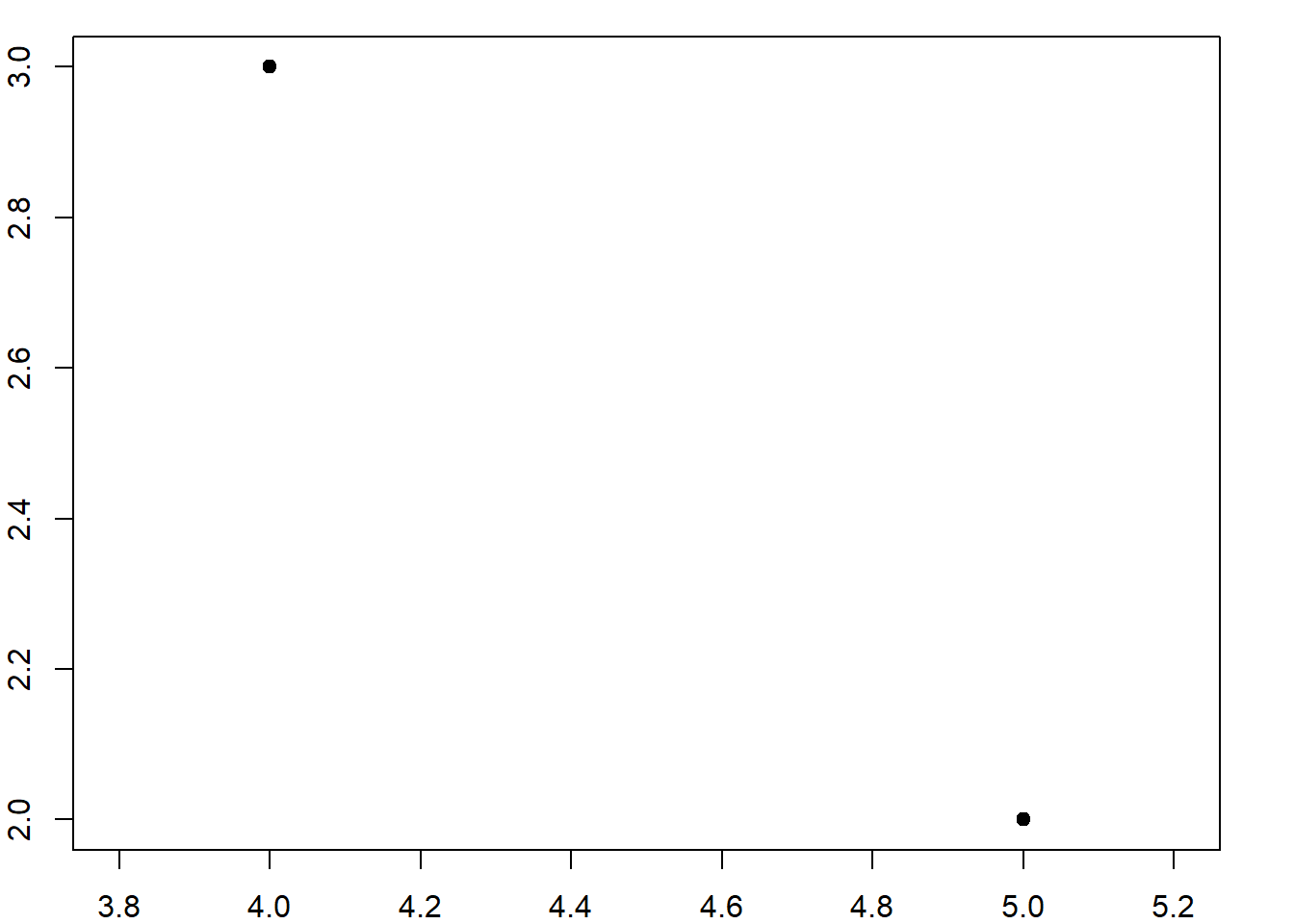

7.3.1.3 Linestring

linea <- sf::st_linestring(matriz_puntos)
linea
LINESTRING (5 2, 4 3)
class(linea)
[1] "XY"         "LINESTRING" "sfg"       
par(mar = c(2,2,1,2))
plot(linea, axes = T, xlab = "X", ylab = "Y")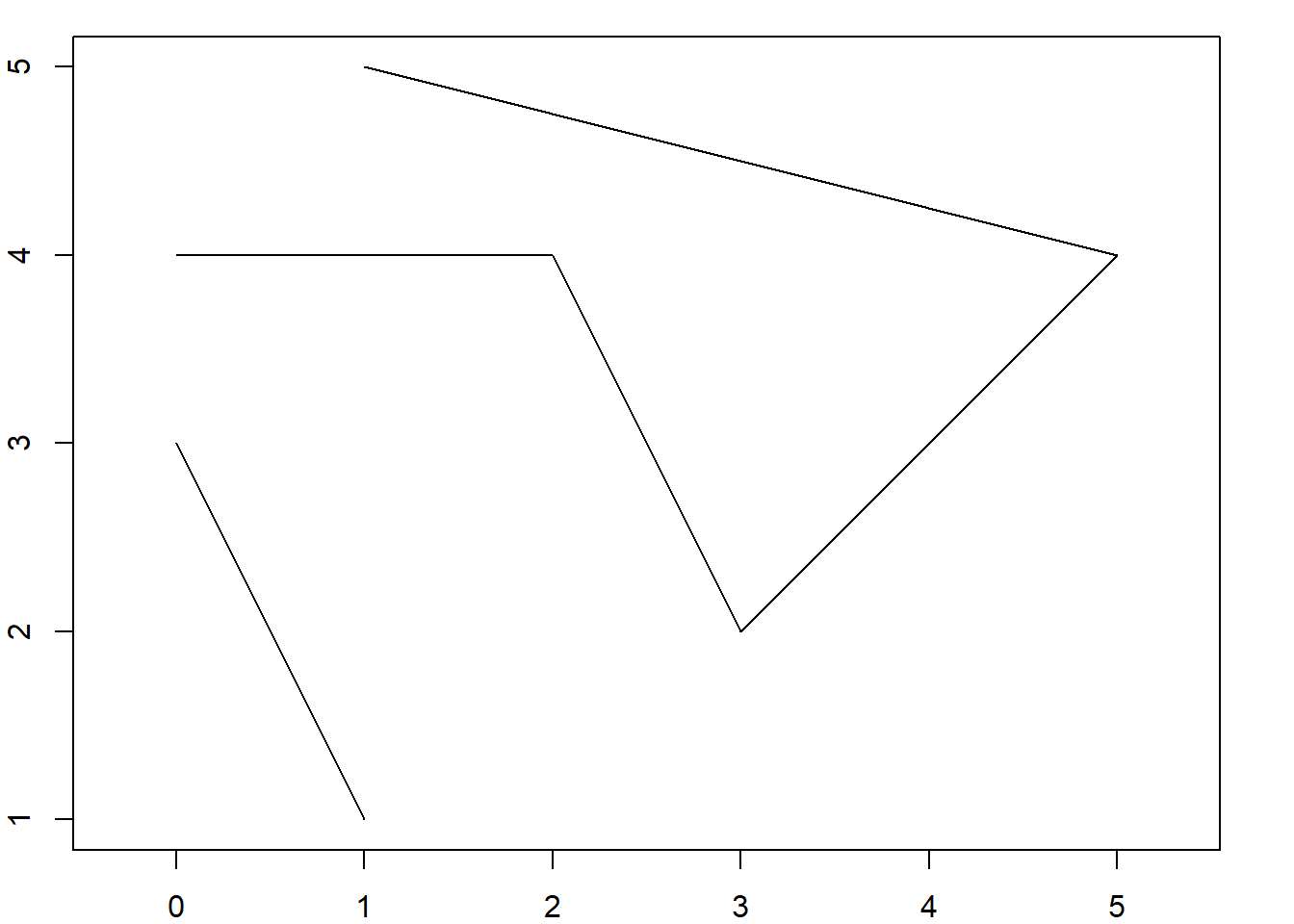

7.3.1.4 Multilinestring

Para generar objetos de tipo multiniestring, polygon, mulipolygon o geometrycollection trabajaremos con listas.

lineas_list <- list(rbind(c(1, 5), c(5, 4), c(3, 2), c(2, 4), c(0, 4)),
                    rbind(c(0, 3), c(1, 1)))
lineas <- st_multilinestring(lineas_list)
class(lineas)
[1] "XY"              "MULTILINESTRING" "sfg"            
par(mar = c(2,2,1,2))
plot(lineas, axes = T, xlab = "X", ylab = "Y")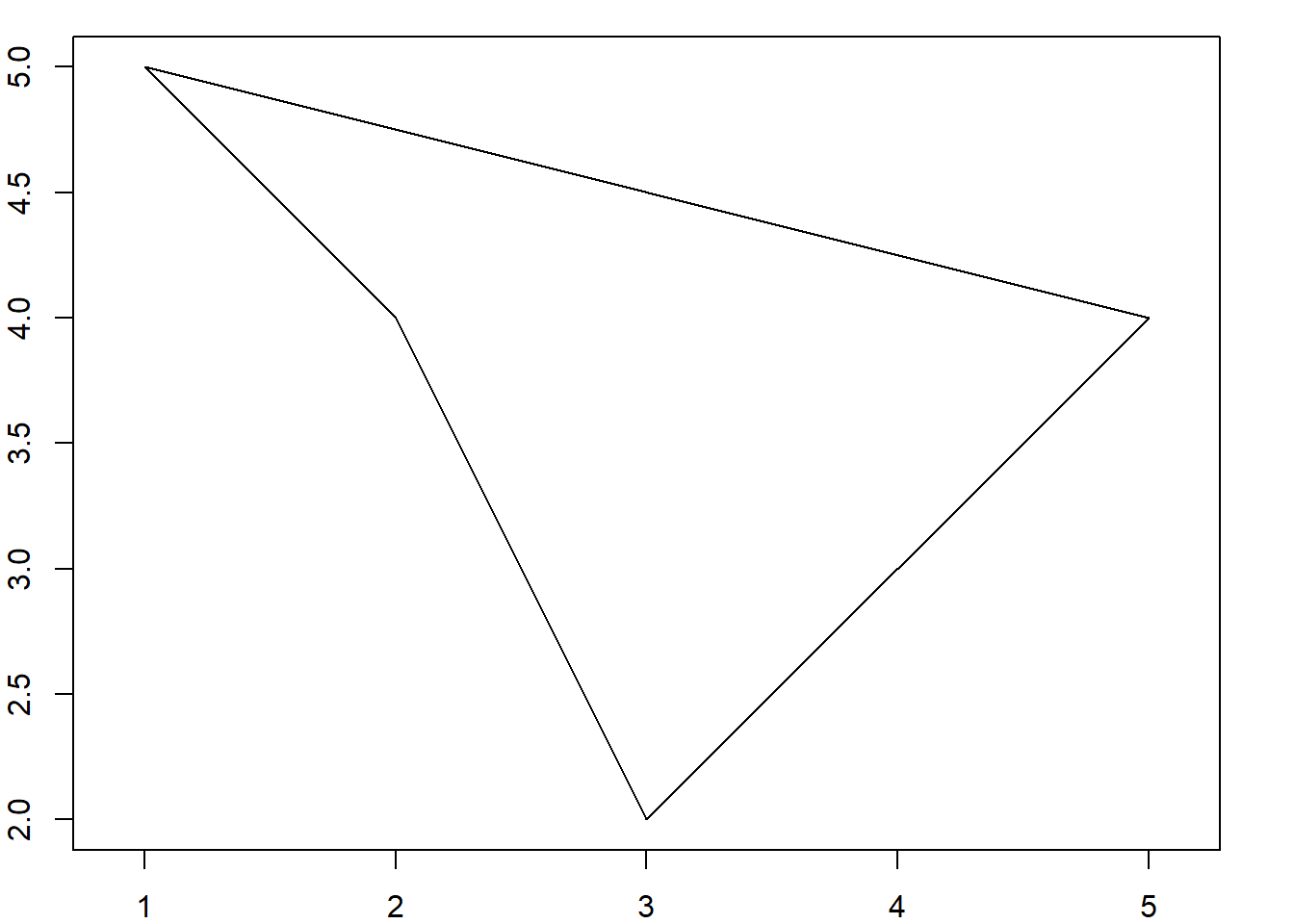

7.3.1.5 Polygon

pol1_list <- list(rbind(c(1, 5), c(5, 4), c(3, 2), c(2, 4), c(1, 5)))
pol1 <- sf::st_polygon(pol1_list)
pol1
POLYGON ((1 5, 5 4, 3 2, 2 4, 1 5))
class(pol1)
[1] "XY"      "POLYGON" "sfg"    
par(mar = c(2,2,1,2))
plot(pol1, axes = T, xlab = "X", ylab = "Y")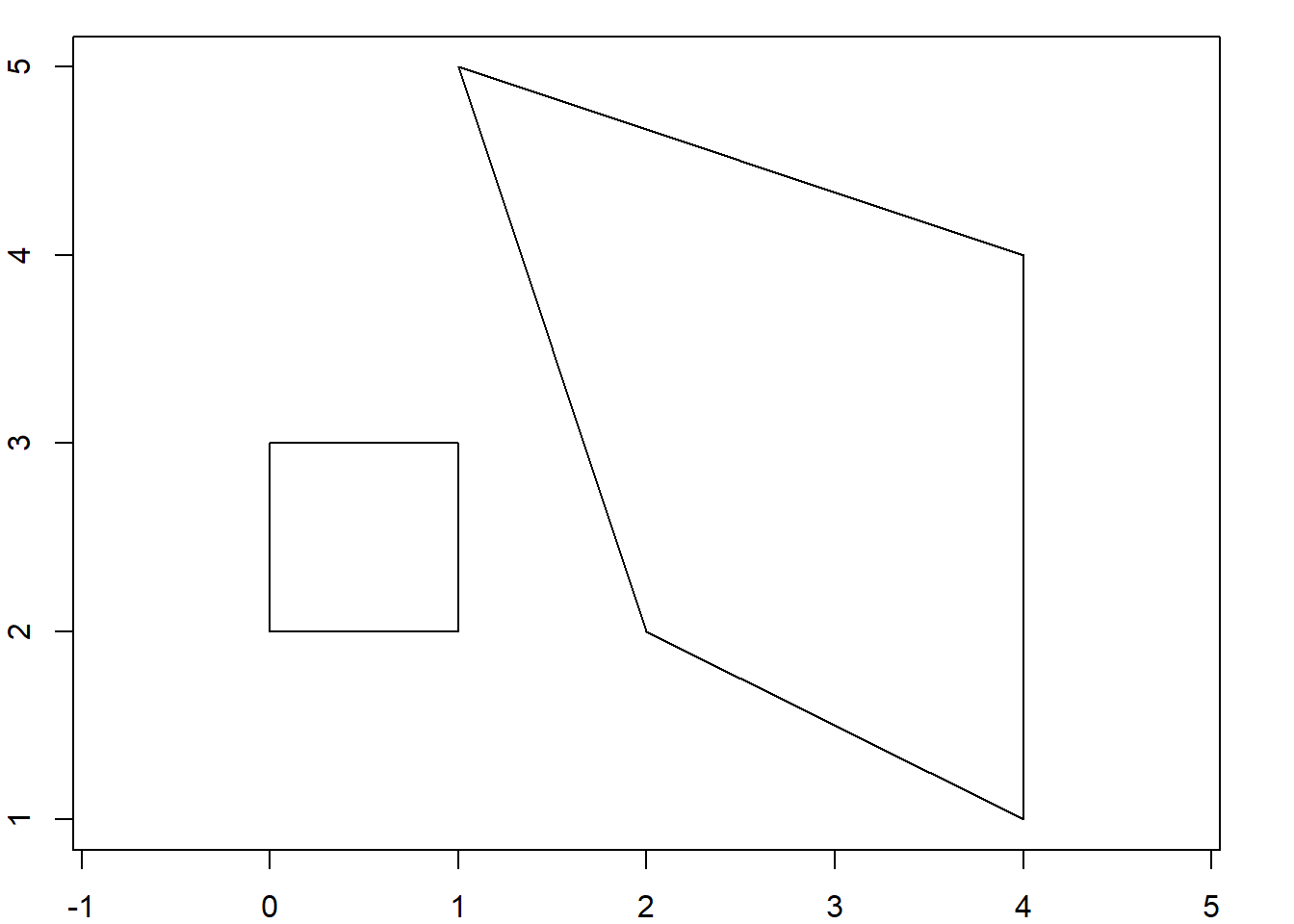

Pregunta

Este polígono tiene 4 puntos, pero hemos puesto 5… ¿Qué ha pasado? ¿Qué pasa si quitamos el quinto punto?

7.3.1.6 Multipolygon

multipolygon_list <- list(list(rbind(c(1, 5), c(2, 2), c(4, 1), c(4, 4), c(1, 5))),
                          list(rbind(c(0, 2), c(1, 2), c(1, 3), c(0, 3), c(0, 2))))
multipoly <- st_multipolygon(multipolygon_list)
multipoly
MULTIPOLYGON (((1 5, 2 2, 4 1, 4 4, 1 5)), ((0 2, 1 2, 1 3, 0 3, 0 2)))
class(multipoly)
[1] "XY"           "MULTIPOLYGON" "sfg"         
par(mar = c(2,2,1,2))
plot(multipoly, axes = T, xlab = "X", ylab = "Y")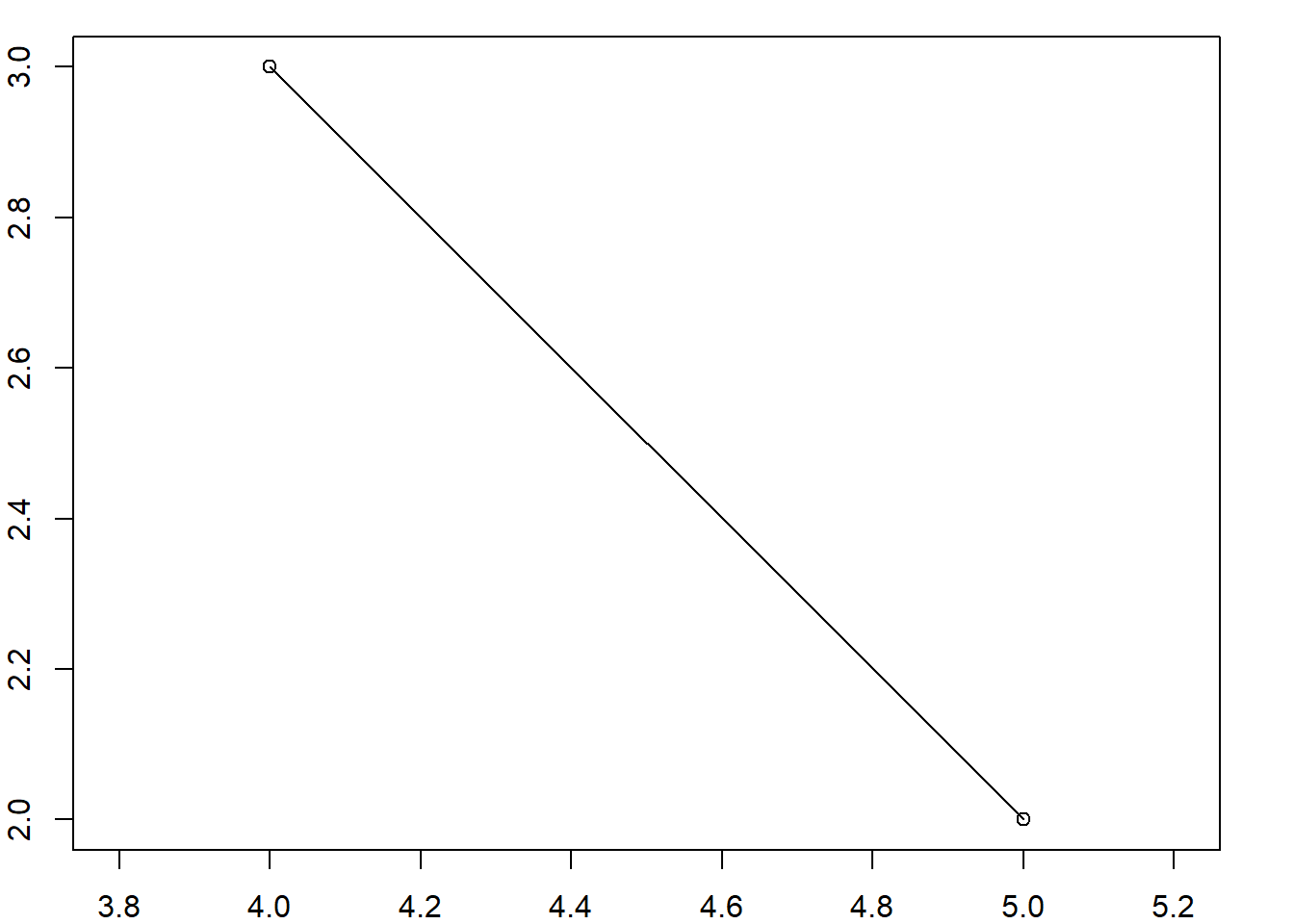

7.3.1.7 Geometrycollection

geom_collection_list <- list(sf::st_multipoint(matriz_puntos),
                             sf::st_linestring(linea))
geom_collection <- sf::st_geometrycollection(geom_collection_list)
geom_collection
GEOMETRYCOLLECTION (MULTIPOINT ((5 2), (4 3)), LINESTRING (5 2, 4 3))
class(geom_collection)
[1] "XY"                 "GEOMETRYCOLLECTION" "sfg"               
par(mar = c(2,2,1,2))
plot(geom_collection, axes = T, xlab = "X", ylab = "Y")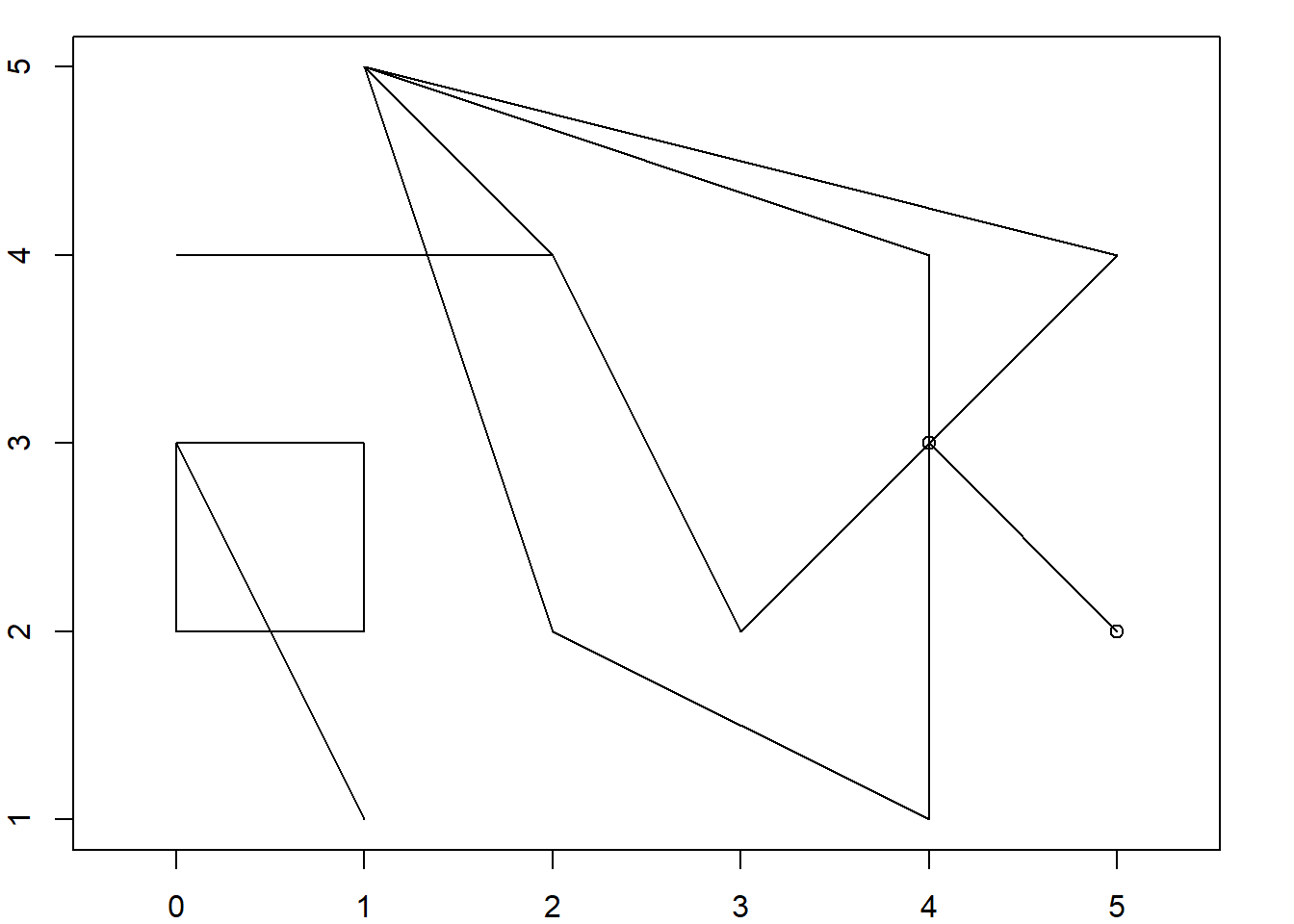

7.3.2 sfc

Como hemos visto en el bloque anterior, un objeto sfg contiene solo una geometría simple (es, por tanto, la unidad más básica de una geometría en el paquete sf). Una sfc (simple feature column) es una lista de objetos sfg (una especie de contenedor que agrupa una o más geometrías sfg), y que además puede contener información sobre el sistema de referencia de coordenadas en uso. Para combinar dos (o más) geometrías simples en un único objeto, podemos usar la función st_sfc().

conjunto <- sf::st_sfc(punto1, punto2, linea, lineas, pol1, multipoly)
conjunto
Geometry set for 6 features 
Geometry type: GEOMETRY
Dimension:     XY
Bounding box:  xmin: 0 ymin: 1 xmax: 5 ymax: 5
CRS:           NA
First 5 geometries:
POINT (5 2)
POINT (4 3)
LINESTRING (5 2, 4 3)
MULTILINESTRING ((1 5, 5 4, 3 2, 2 4, 0 4), (0 ...
POLYGON ((1 5, 5 4, 3 2, 2 4, 1 5))
class(conjunto)
[1] "sfc_GEOMETRY" "sfc"         
par(mar = c(2,2,1,2))
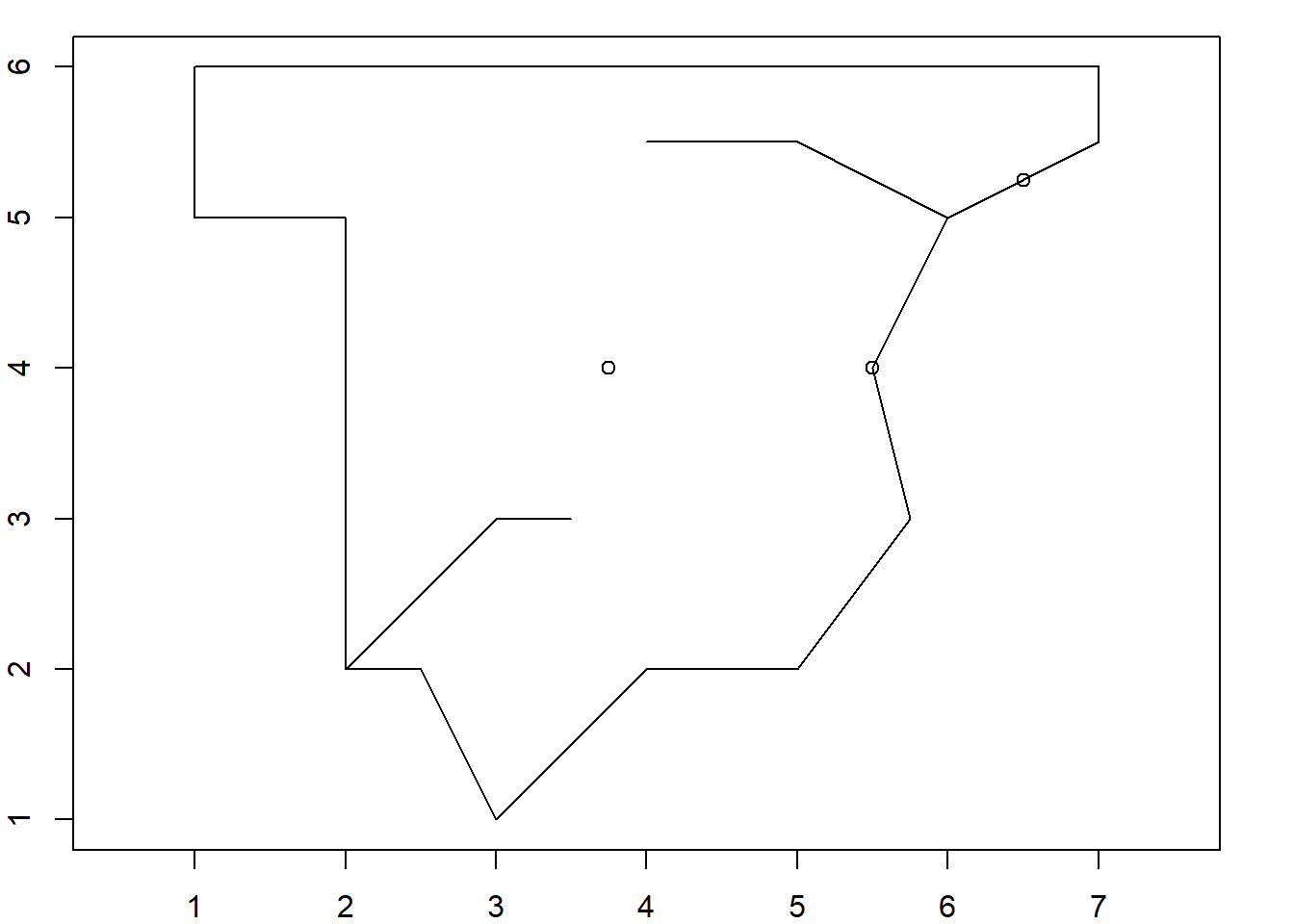
plot(conjunto, axes = T, xlab = "X", ylab = "Y")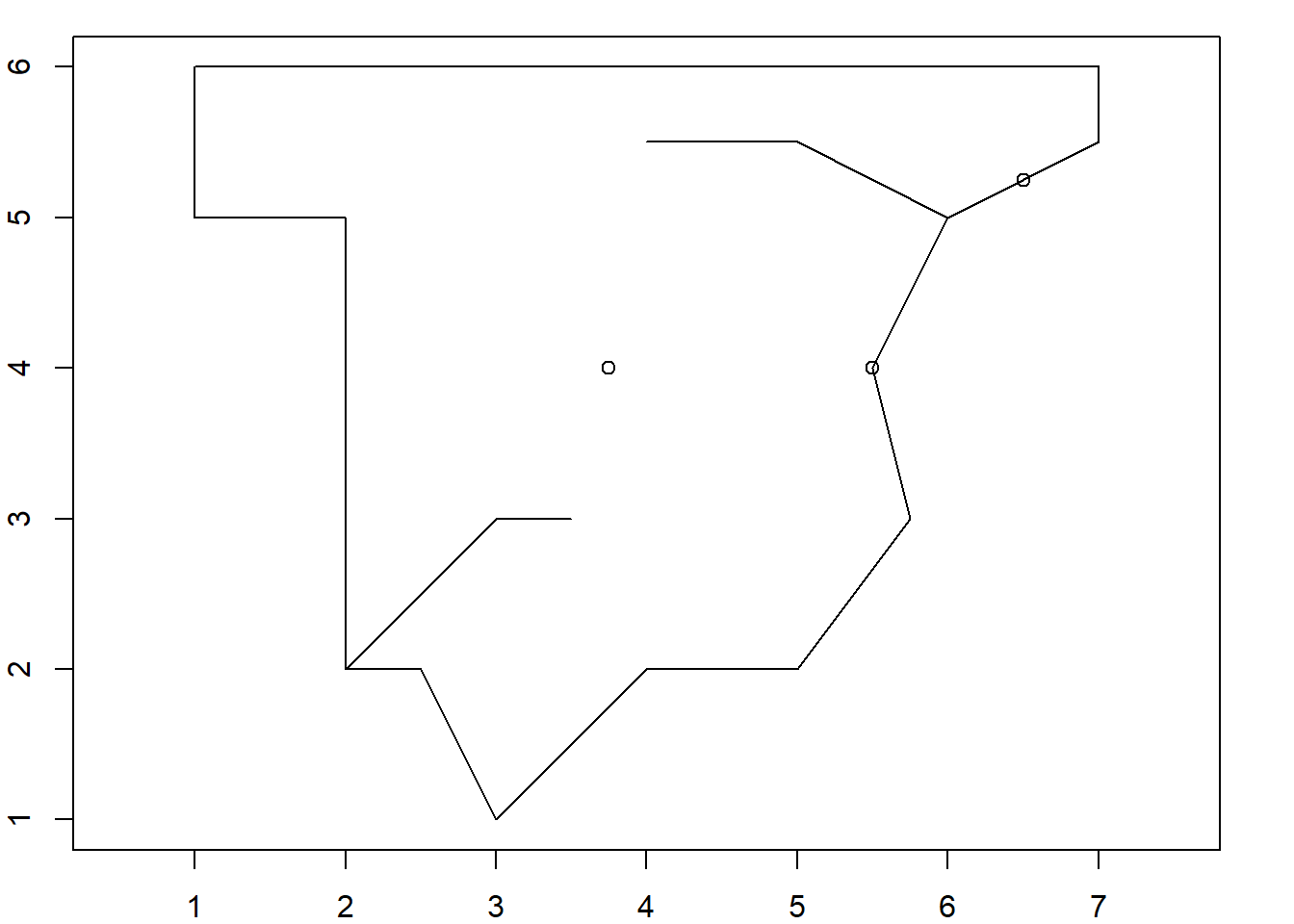

Ejercicio

Crea la siguiente figura:

7.3.3 sfc + CRS

Pregunta

Observemos el objeto creado… ¿Hay algo que te llame la atención?

Para ver qué CRS tiene asignado un objeto, usaremos la función st_crs:

sf::st_crs(geom_col)
Coordinate Reference System: NA

Como dijimos anteriormente, es posible asignar un sistema de coordenadas de referencia al objeto sfc. De hecho, suele ser lo habitual.

Para asignar un CRS a un objeto que aun no tiene asignado ninguno, también se usa la función st_crs:

sf::st_crs(geom_col) <- 4326

Para modificar el CRS de un objeto que ya tiene uno asignado, se usa la función st_transform():

geom_col2 <- sf::st_transform(geom_col, crs = 4258)
sf::st_crs(geom_col2)
Coordinate Reference System:
  User input: EPSG:4258 
  wkt:
GEOGCRS["ETRS89",
    ENSEMBLE["European Terrestrial Reference System 1989 ensemble",
        MEMBER["European Terrestrial Reference Frame 1989"],
        MEMBER["European Terrestrial Reference Frame 1990"],
        MEMBER["European Terrestrial Reference Frame 1991"],
        MEMBER["European Terrestrial Reference Frame 1992"],
        MEMBER["European Terrestrial Reference Frame 1993"],
        MEMBER["European Terrestrial Reference Frame 1994"],
        MEMBER["European Terrestrial Reference Frame 1996"],
        MEMBER["European Terrestrial Reference Frame 1997"],
        MEMBER["European Terrestrial Reference Frame 2000"],
        MEMBER["European Terrestrial Reference Frame 2005"],
        MEMBER["European Terrestrial Reference Frame 2014"],
        MEMBER["European Terrestrial Reference Frame 2020"],
        ELLIPSOID["GRS 1980",6378137,298.257222101,
            LENGTHUNIT["metre",1]],
        ENSEMBLEACCURACY[0.1]],
    PRIMEM["Greenwich",0,
        ANGLEUNIT["degree",0.0174532925199433]],
    CS[ellipsoidal,2],
        AXIS["geodetic latitude (Lat)",north,
            ORDER[1],
            ANGLEUNIT["degree",0.0174532925199433]],
        AXIS["geodetic longitude (Lon)",east,
            ORDER[2],
            ANGLEUNIT["degree",0.0174532925199433]],
    USAGE[
        SCOPE["Spatial referencing."],
        AREA["Europe - onshore and offshore: Albania; Andorra; Austria; Belgium; Bosnia and Herzegovina; Bulgaria; Croatia; Cyprus; Czechia; Denmark; Estonia; Faroe Islands; Finland; France; Germany; Gibraltar; Greece; Hungary; Ireland; Italy; Kosovo; Latvia; Liechtenstein; Lithuania; Luxembourg; Malta; Moldova; Monaco; Montenegro; Netherlands; North Macedonia; Norway including Svalbard and Jan Mayen; Poland; Portugal; Romania; San Marino; Serbia; Slovakia; Slovenia; Spain; Sweden; Switzerland; United Kingdom (UK) including Channel Islands and Isle of Man; Vatican City State."],
        BBOX[32.88,-16.1,84.73,40.18]],
    ID["EPSG",4258]]
Pregunta

¿Qué CRS conoces?

7.3.4 sf

Siguiendo el diagrama inicial, nos queda un último paso para crear un objeto sf. Para ello, lo único que faltaría sería añadir un data.frame al objeto sfc que ya tenemos.

Pregunta

¿Qué información le añadirías?

data <- data.frame(nombre = c("Valencia","Madrid","Barcelona","Ebro","Guadiana","España"),
                   tipo = c(rep("ciudad",3), rep("rio",2), "pais"))
data
     nombre   tipo
1  Valencia ciudad
2    Madrid ciudad
3 Barcelona ciudad
4      Ebro    rio
5  Guadiana    rio
6    España   pais
objeto_sf <- sf::st_sf(data, geom_col)
class(objeto_sf)
[1] "sf"         "data.frame"

Ahora ya tenemos nuestro objeto sf, el cual podemos representar gráficamente con ggplot2:

library(ggplot2)

ggplot() +
  geom_sf(data = objeto_sf)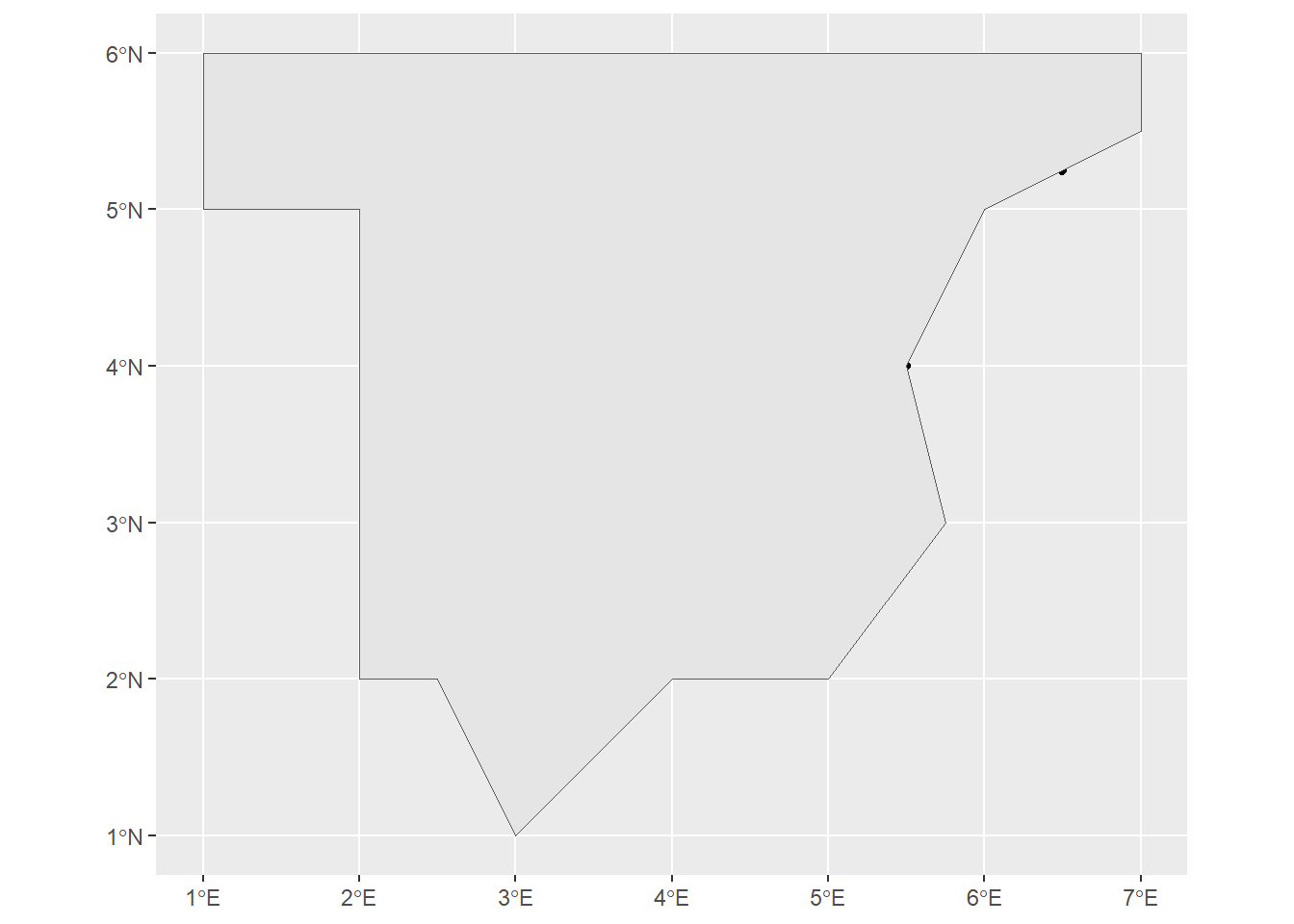

Pregunta

¿Qué problemas ves en el gráfico?

Digamos que el objeto sf que hemos creado “mezcla” información (datos) de diversa índole. Lo recomendable es tener un objeto para cada tipo de datos (puntos, líneas, polígonos) y luego usar lo que necesitemos.

library(dplyr)
sf1 <- objeto_sf %>% filter(tipo == "ciudad")
sf2 <- objeto_sf %>% filter(tipo == "rio")
sf3 <- objeto_sf %>% filter(tipo == "pais")

Teniendo la información estructurada correctamente, podemos representarla mejor:

ggplot() +
  geom_sf(data = sf3, fill="white") +
  geom_sf(data = sf2, color="blue") +
  geom_sf(data = sf1, shape=19, color="red")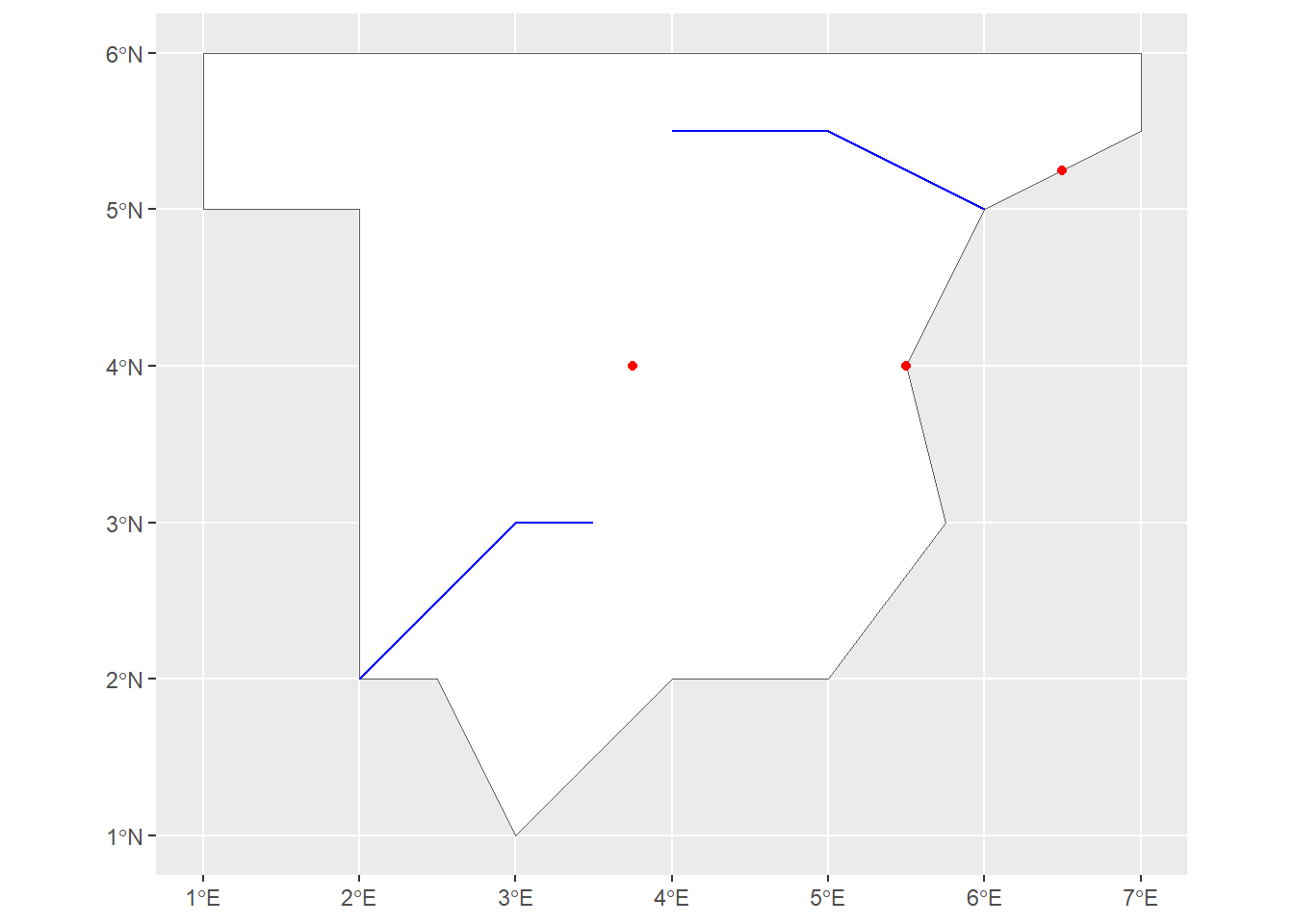

7.3.5 Descomponer un objeto sf

Ya hemos visto los pasos para crear un objeto sf pero, ¿cómo podemos extraer los datos (data.frame)? ¿y las geometrías?

Para lo primero usaremos la función st_set_geometry(). Para lo segundo, la función st_geometry():

datos <- sf::st_set_geometry(objeto_sf, NULL)
class(datos)
[1] "data.frame"
datos
     nombre   tipo
1  Valencia ciudad
2    Madrid ciudad
3 Barcelona ciudad
4      Ebro    rio
5  Guadiana    rio
6    España   pais
geom <- sf::st_geometry(objeto_sf)
class(geom)
[1] "sfc_GEOMETRY" "sfc"

7.4 Resumen

En este apartado hemos visto las siguientes funciones del paquete sf:

  • st_point
  • st_multipoint
  • st_linestring
  • st_multilinestring
  • st_polygon
  • st_multipolygon
  • st_geometrycollection
  • st_sfc
  • st_crs
  • st_transform
  • st_sf
  • st_set_geometry
  • st_geometry
  • st_drop_geometry
Ejercicio

¿Para qué sirve cada una de estas funciones?

Bivand, R., Keitt, T., y Rowlingson, B. (2017). rgdal: Bindings for the ’Geospatial’ Data Abstraction Library. https://CRAN.R-project.org/package=rgdal
Pebesma, E. (2018). Simple Features for R: Standardized Support for Spatial Vector Data. The R Journal, 10(1), 439-446. https://doi.org/10.32614/RJ-2018-009
Pebesma, E. (2022). sf: Simple Features for R. https://CRAN.R-project.org/package=sf
Pebesma, E., y Bivand, R. (2023). sp: Classes and Methods for Spatial Data. https://CRAN.R-project.org/package=sp
Wickham, H. (2016). ggplot2: elegant graphics for data analysis. Springer.
Wickham, H., François, R., Henry, L., Müller, K., y Vaughan, D. (2023). dplyr: A Grammar of Data Manipulation. https://CRAN.R-project.org/package=dplyr
Wickham, H., Vaughan, D., y Girlich, M. (2023). tidyr: Tidy Messy Data. https://CRAN.R-project.org/package=tidyr