library(dplyr)
leaflet::leaflet() %>%
leaflet::addProviderTiles("Esri.WorldImagery") %>%
leaflet::addMarkers(lng = 5.736411469027462,
lat = 50.97762112889899,
label = "Río Mosa - Meuse River") %>%
leaflet::setView(lng = 5.739371512344707,
lat = 50.97421490588442,
zoom = 13)14 Geoestadística
14.1 Introducción
En esta práctica nos centraremos en predecir la distribución espacial de variables continuas asociadas a fenómenos cuantificables. Para ello utilizaremos el conjunto de datos Meuse del paquete sp. Los datos corresponden a localizaciones y concentraciones de metales pesados en la capa superior del suelo (en un área de aproximadamente de 15 × 15 metros), recogidos en una llanura de inundación del río Mosa, cerca de la localidad holandesa de Stein.
14.2 Paquetes
En esta práctica utilizaremos funciones de las siguientes librerías:
library(tidyverse)
library(sf)
library(sp)
library(gstat)14.3 Análisis exploratorio
En primer lugar, obtenemos el conjunto de datos con el que vamos a trabajar:
#data(package="sp")
data(meuse)Las dos primeras columnas del dataframe son las localizaciones en coordenadas RDH (un sistema de coordenadas topográficas holandés); las cuatro siguientes, concentraciones en partes por millón de metales pesados (cadmio, cobre, plomo y zinc); elev es la elevación relativa sobre la llanura; dist es la distancia GIS al río Mosa; om es la materia orgánica del suelo; las cuatro siguientes son variables de tipo cualitativo, mientras que la última dist.m es la distancia en metros al río Mosa. Toda esta información está disponible en el manual de referencia del paquete sp.
?meusestarting httpd help server ... doneglimpse(meuse)Rows: 155
Columns: 14
$ x <dbl> 181072, 181025, 181165, 181298, 181307, 181390, 18…
$ y <dbl> 333611, 333558, 333537, 333484, 333330, 333260, 33…
$ cadmium <dbl> 11.7, 8.6, 6.5, 2.6, 2.8, 3.0, 3.2, 2.8, 2.4, 1.6,…
$ copper <dbl> 85, 81, 68, 81, 48, 61, 31, 29, 37, 24, 25, 25, 93…
$ lead <dbl> 299, 277, 199, 116, 117, 137, 132, 150, 133, 80, 8…
$ zinc <dbl> 1022, 1141, 640, 257, 269, 281, 346, 406, 347, 183…
$ elev <dbl> 7.909, 6.983, 7.800, 7.655, 7.480, 7.791, 8.217, 8…
$ dist <dbl> 0.00135803, 0.01222430, 0.10302900, 0.19009400, 0.…
$ om <dbl> 13.6, 14.0, 13.0, 8.0, 8.7, 7.8, 9.2, 9.5, 10.6, 6…
$ ffreq <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ soil <fct> 1, 1, 1, 2, 2, 2, 2, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1,…
$ lime <fct> 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1,…
$ landuse <fct> Ah, Ah, Ah, Ga, Ah, Ga, Ah, Ab, Ab, W, Fh, Ag, W, …
$ dist.m <dbl> 50, 30, 150, 270, 380, 470, 240, 120, 240, 420, 40…Vamos a centrarnos en la variable zinc. Primero exploramos la variable y generamos un histograma. Como se puede observar, la distribución no es simétrica (está sesgada hacia la derecha). Esto también lo podemos observar haciendo un summary(), puesto que la media es mayor que la mediana (distribución no-normal).
hist(meuse$zinc, breaks = 16)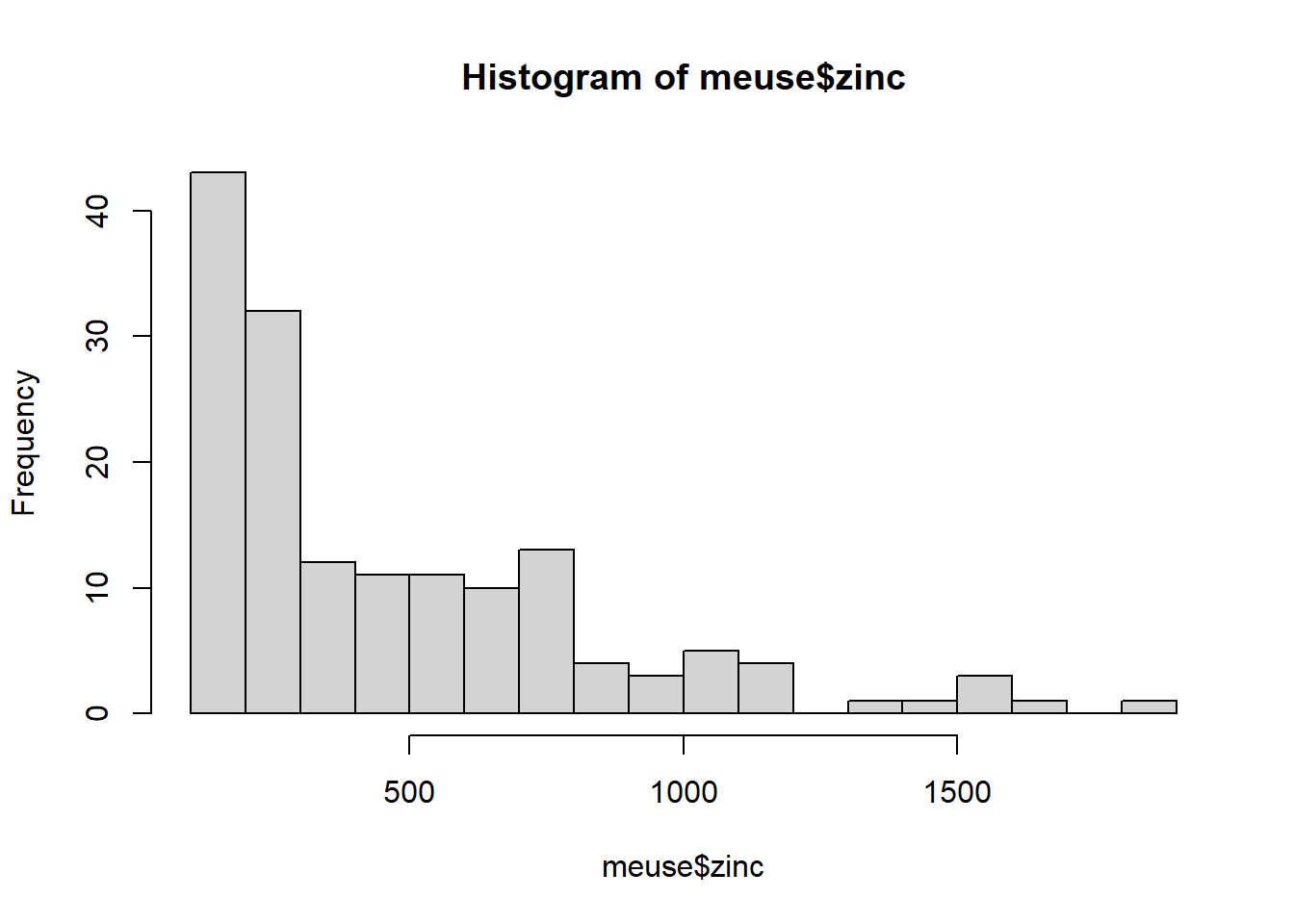
summary(meuse$zinc) Min. 1st Qu. Median Mean 3rd Qu. Max.
113.0 198.0 326.0 469.7 674.5 1839.0 Al ser una distribución no simétrica, se aplica el logaritmo para transformar los valores y obtener una distribución simétrica (Normal). Esto, ademas, reduce los posibles outliers.
meuse <- meuse %>%
mutate(logZn = log10(zinc)) %>%
relocate(logZn, .after = zinc)
hist(meuse$logZn, breaks = 16)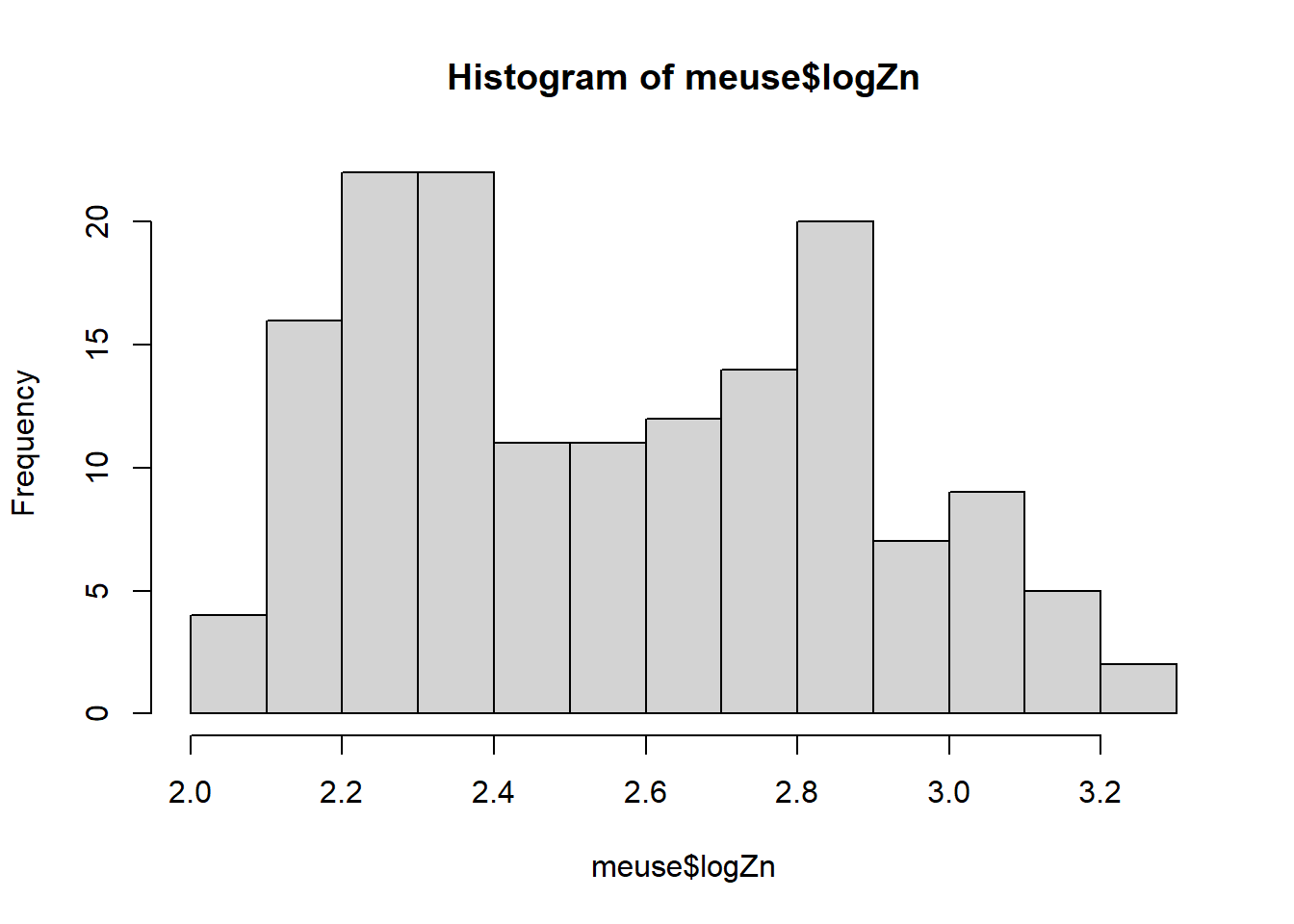
summary(meuse$logZn) Min. 1st Qu. Median Mean 3rd Qu. Max.
2.053 2.297 2.513 2.556 2.829 3.265 14.4 Estructura espacial
Lo primero que debemos hacer es georreferenciar los datos, usando algunas funciones del paquete sf.
class(meuse)[1] "data.frame"meuse.sf <- st_as_sf(meuse, coords = c("x","y"))
class(meuse.sf)[1] "sf" "data.frame"st_crs(meuse.sf)Coordinate Reference System: NAst_crs(meuse.sf) <- 28992 # https://epsg.io/28992A continuación, visualizaremos la distribución espacial de los puntos. Los puntos no están regularmente distribuidos sino que existe una mayor densidad en las proximidades del río.
data(meuse.riv, package="sp")
class(meuse.riv)[1] "matrix" "array" meuse.riv.sf <- st_sfc(st_linestring(meuse.riv, dim="XY"), crs = st_crs(meuse.sf))
class(meuse.riv.sf)[1] "sfc_LINESTRING" "sfc" summary(meuse.riv.sf) LINESTRING epsg:28992 +proj=ster...
1 0 0 ggplot() +
geom_sf(data = meuse.sf, mapping = aes(size=zinc, color=dist.m)) +
geom_sf(data = meuse.riv.sf) +
labs(color = "Distancia al río (metros)",
size = "Concentración de Zinc (en ppm)") +
theme_void()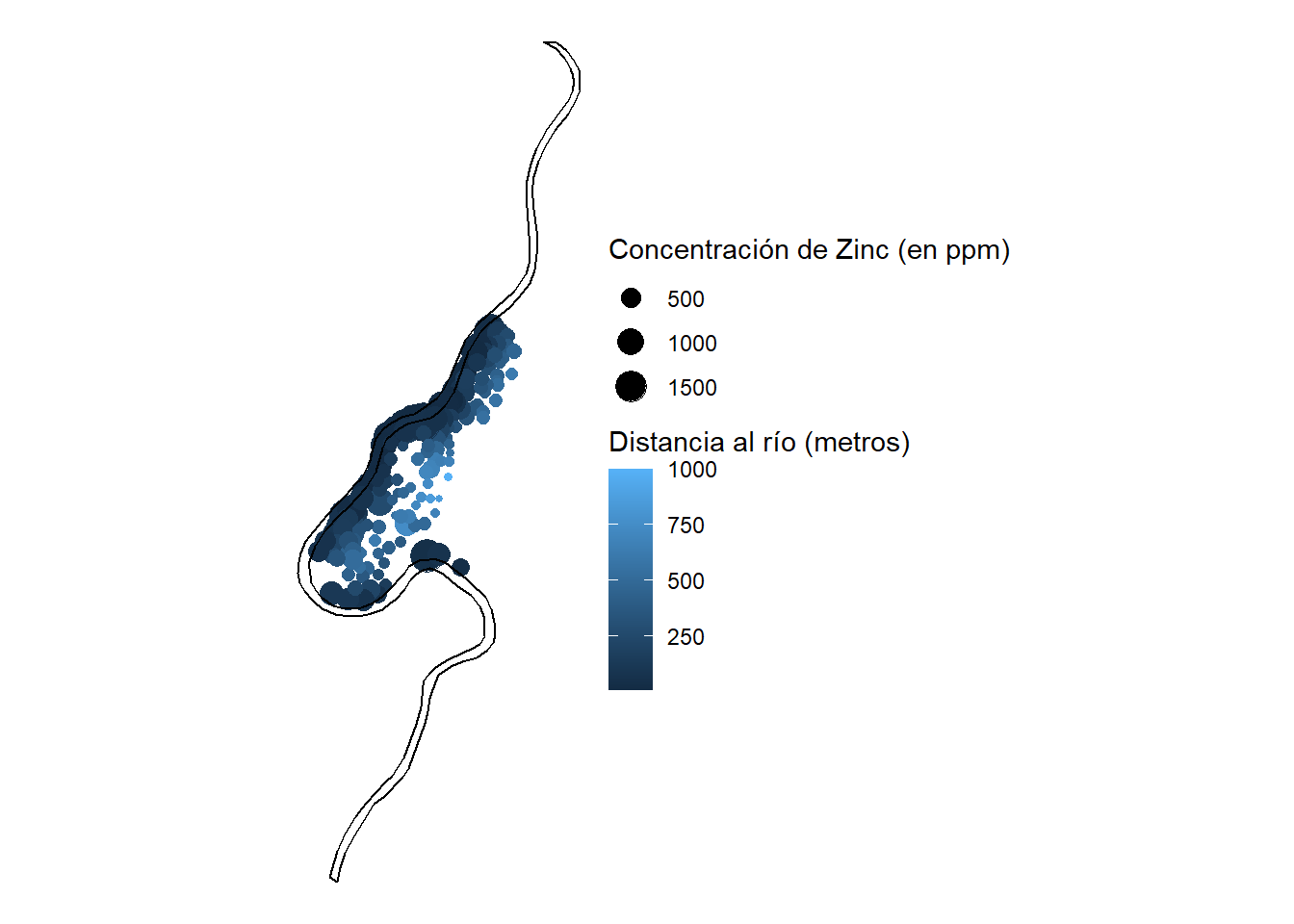
Como vimos en la teoría, la dependencia espacial local significa que cuanto más cerca estén los puntos en el espacio geográfico, más cerca también lo están en el espacio de atributos. Esto se llama autocorrelación.
Los valores de un atributo pueden estar correlacionados con sí mismos, y la fuerza de esta correlación depende de la distancia de separación entre puntos.
Cada par de puntos, estará separado por una distancia en el espacio geográfico y una semivarianza en el espacio de atributos.
14.5 Cálculo de la semivarianza
La expresión de la semivarianza, tal y como vimos en la teoría, es:
\[ \gamma(s)=\frac{1}{2}(z_i-z_j)^2 \]
¿Cuántos pares de puntos hay en el conjunto de datos?
n <- length(meuse.sf$logZn)
n*(n-1)/2[1] 11935Calculamos la distancia y la semivarianza para los primeros dos puntos del dataset:
dim(st_coordinates(meuse.sf))[1] 155 2i <- st_coordinates(meuse.sf)[1,] #coordenadas del primer punto
j <- st_coordinates(meuse.sf)[2,] #coordenadas del segundo punto
sep <- dist(st_coordinates(meuse.sf)[1:2,]) #distancia entre ambos puntos
(gamma <- 0.5 * (meuse.sf$logZn[1] - meuse.sf$logZn[2])^2) # semivarianza, unidades log(mg kg-1)^2[1] 0.001144082Ahora graficaremos el variograma experimental, teniendo en cuenta las concentraciones de Zinc (en log). Recordemos que el variograma es una representación gráfica que agrupa los pares de puntos por intervalos de distancia, calculando la media de todas las semivarianzas para cada intervalo. En este caso fijamos los intervalos (width) en una distancia de 100 metros, hasta una distancia máxima (cutoff) de 1600 metros. Por defecto, la función variogram() usa un valor de cutoff igual a la tercera parte de la diagonal del bounding box del conjunto de puntos, y lo divide en 15 partes para obtener el valor de width. Comentar que la función variogram() lo que realmente genera es la nube de variograma, pero como vimos en la teoría, no aporta mucha información:
(ve <- variogram(logZn ~ 1, meuse.sf)) np dist gamma dir.hor dir.ver id
1 57 79.29244 0.02328372 0 0 var1
2 299 163.97367 0.04078134 0 0 var1
3 419 267.36483 0.05710896 0 0 var1
4 457 372.73542 0.07773532 0 0 var1
5 547 478.47670 0.08740507 0 0 var1
6 533 585.34058 0.10650776 0 0 var1
7 574 693.14526 0.10731407 0 0 var1
8 564 796.18365 0.11668969 0 0 var1
9 589 903.14650 0.12205966 0 0 var1
10 543 1011.29177 0.13043828 0 0 var1
11 500 1117.86235 0.13266916 0 0 var1
12 477 1221.32810 0.11389827 0 0 var1
13 452 1329.16407 0.12292122 0 0 var1
14 457 1437.25620 0.10685452 0 0 var1
15 415 1543.20248 0.10841829 0 0 var1(ve <- variogram(logZn ~ 1, meuse.sf, cutoff = 1600, width = 100)) np dist gamma dir.hor dir.ver id
1 52 77.01898 0.02451310 0 0 var1
2 263 156.23373 0.03944162 0 0 var1
3 381 252.07842 0.05567101 0 0 var1
4 430 351.32465 0.07233142 0 0 var1
5 475 449.81046 0.08320925 0 0 var1
6 503 547.38671 0.09831169 0 0 var1
7 525 648.91763 0.10411787 0 0 var1
8 565 749.37405 0.11606559 0 0 var1
9 535 851.35872 0.12769093 0 0 var1
10 530 950.02457 0.12146261 0 0 var1
11 487 1048.66466 0.13023823 0 0 var1
12 483 1150.81781 0.12656410 0 0 var1
13 431 1249.49976 0.11800227 0 0 var1
14 419 1348.75136 0.11961576 0 0 var1
15 427 1449.84210 0.10647697 0 0 var1
16 386 1549.20766 0.10871425 0 0 var1plot(ve, plot.numbers = TRUE, pch = 20,
xlab = "distancia",
ylab = "semivarianza [log10(Zn)^2]")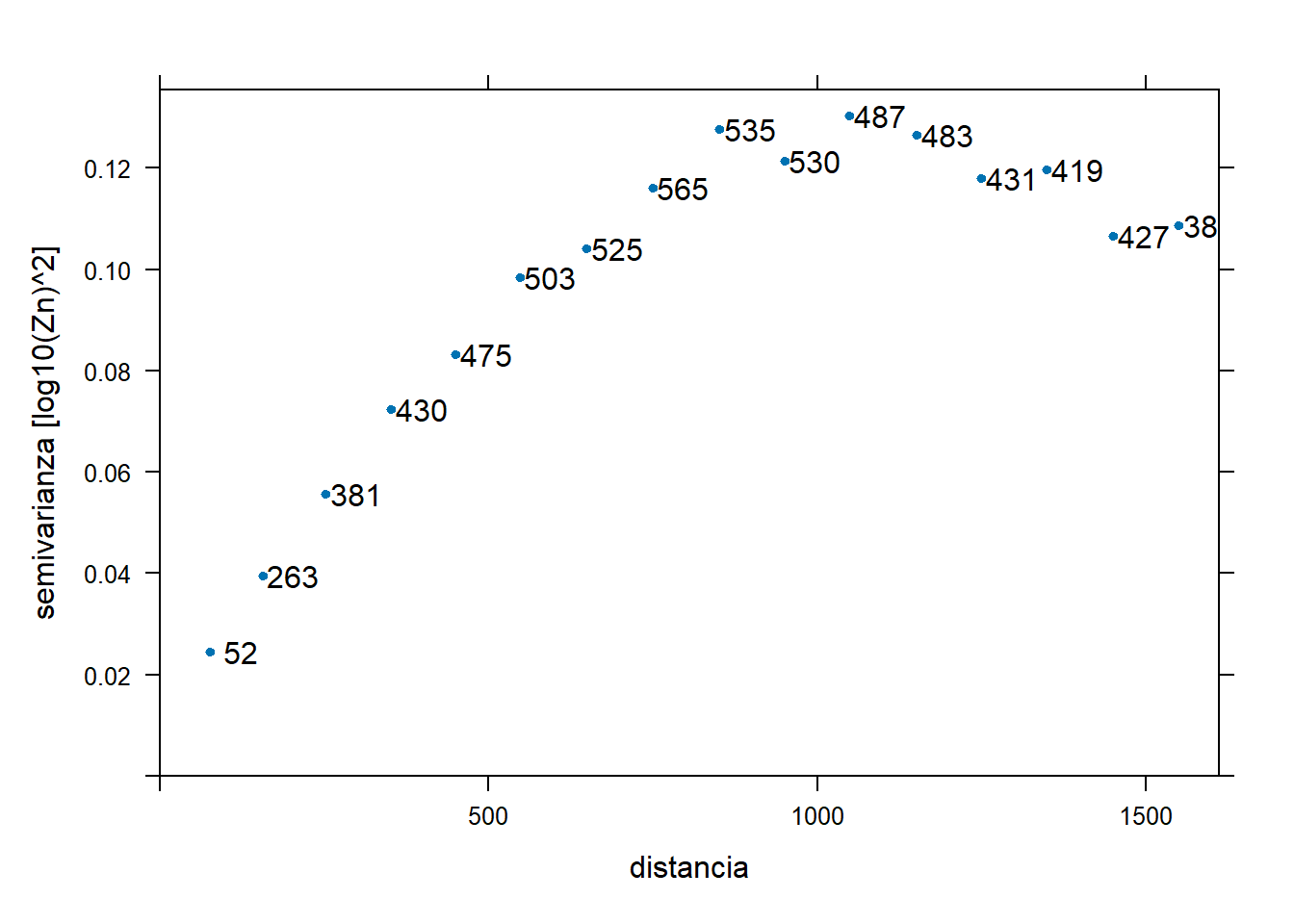
#diagonal del bounding box
min <- st_point(c(st_bbox(meuse.sf)[1],st_bbox(meuse.sf)[2]))
max <- st_point(c(st_bbox(meuse.sf)[3],st_bbox(meuse.sf)[4]))
st_distance(min,max) [,1]
[1,] 4789.868plot(variogram(logZn ~ 1, meuse.sf, cloud=TRUE), pch = 20,
xlab = "distancia",
ylab = "semivarianza")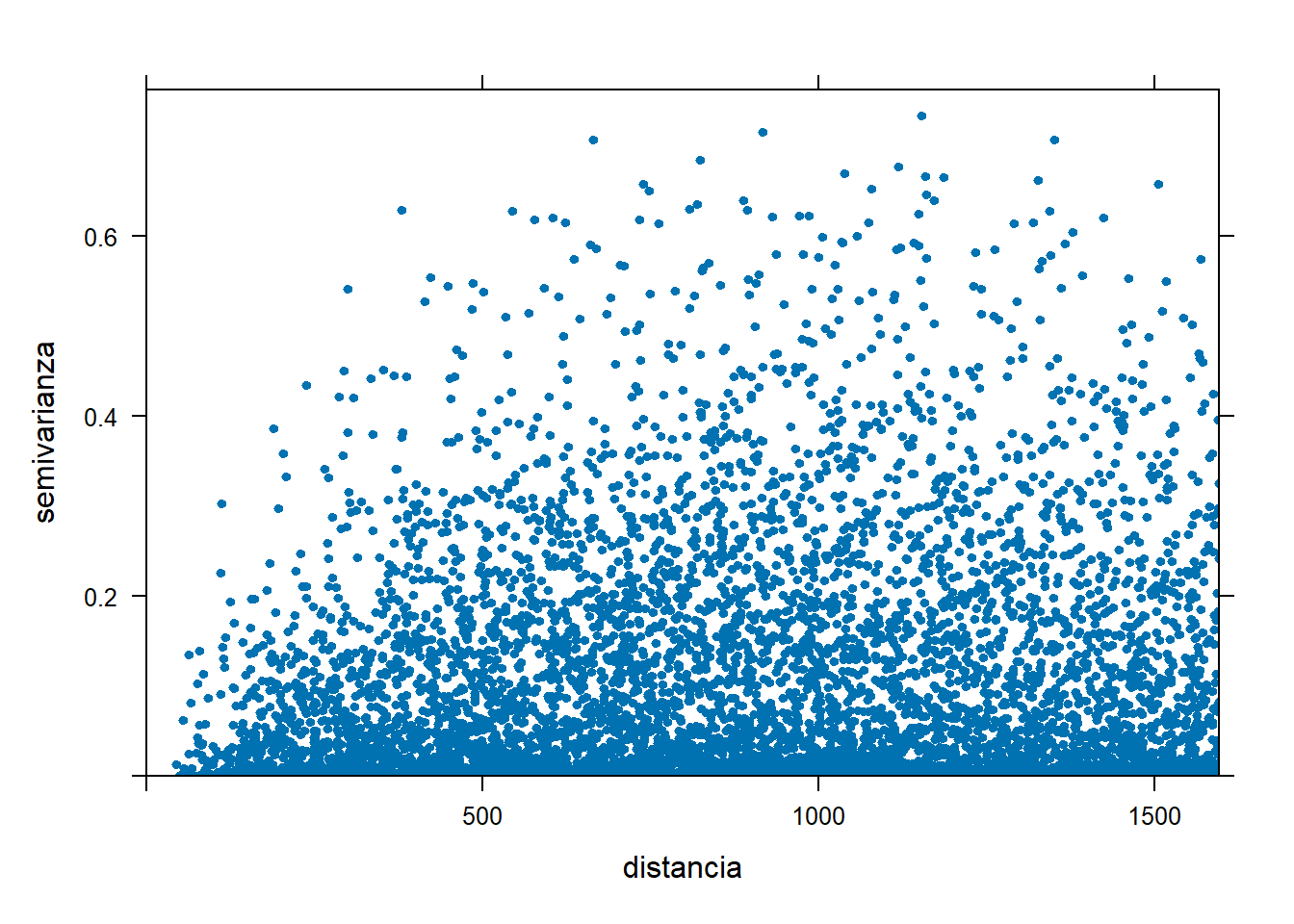
También podemos mostrar con la función variogram() los pares de puntos que están más próximos/lejanos entre sí:
vc <- variogram(logZn ~ 1, meuse.sf, cloud=TRUE)
min(vc$dist)[1] 43.93177max(vc$dist)[1] 1596.091vc <- vc %>% arrange(dist)
head(vc) dist gamma dir.hor dir.ver id left right
1 43.93177 1.326441e-02 0 0 var1 87 72
2 49.24429 8.749351e-05 0 0 var1 26 25
3 53.00000 2.375806e-03 0 0 var1 23 22
4 55.22681 6.198261e-02 0 0 var1 88 79
5 56.04463 8.764773e-03 0 0 var1 88 73
6 56.36488 2.996326e-03 0 0 var1 139 77tail(vc) dist gamma dir.hor dir.ver id left right
6878 1595.350 0.32538378 0 0 var1 108 38
6879 1595.509 0.03284066 0 0 var1 149 104
6880 1595.600 0.03340535 0 0 var1 155 76
6881 1595.741 0.24158867 0 0 var1 107 78
6882 1595.846 0.08290377 0 0 var1 108 90
6883 1596.091 0.01524721 0 0 var1 140 120Y verificar que distancia y semivarianza tienen una relación positiva:
ggplot(data = vc, aes(x=dist, y=gamma)) +
geom_point(color="grey80") +
geom_smooth(method='lm', formula=y~x) +
theme_classic()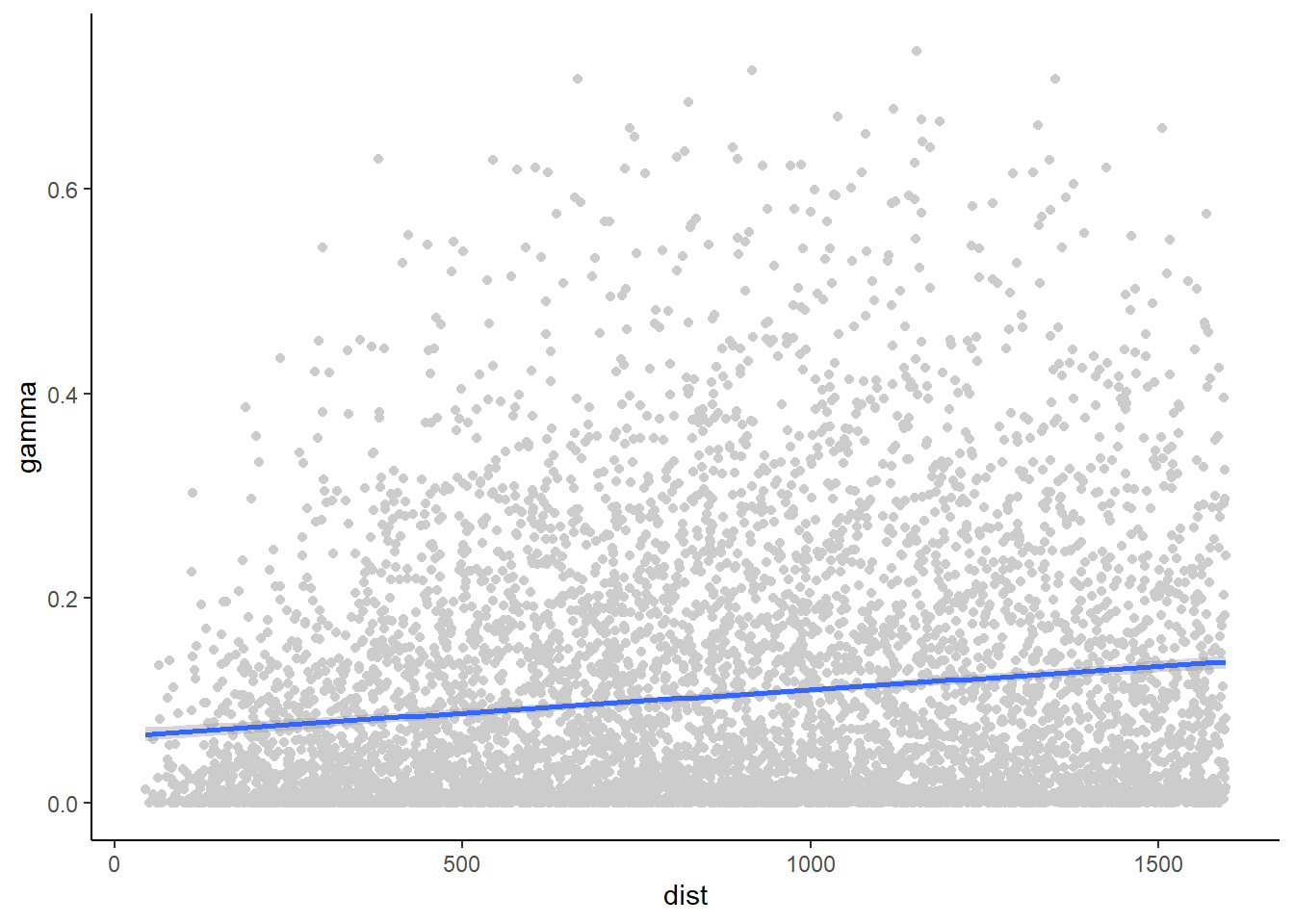
Pero, ¿cómo se relacionan las semivarianzas respecto de las distancias?
Para saberlo, debemos comparar nuestro viariograma experimiental con los distintos variogramas teóricos existentes. Primero, veamos los diferentes tipos:
print(show.vgms())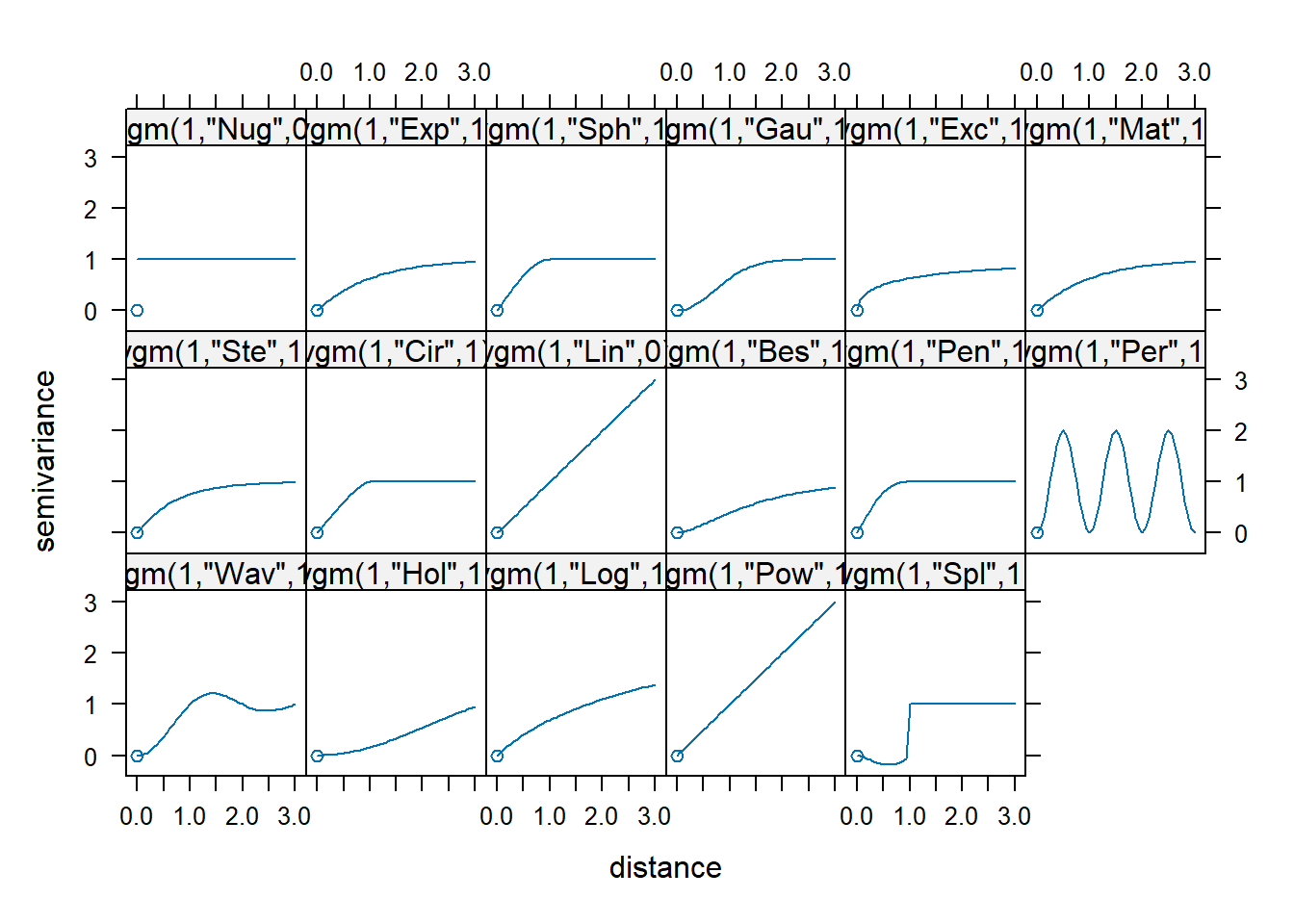
Una vez tenemos claro qué modelo se asemeja más a nuestro variograma experimental, lo generamos. Para ello, debemos introducir los parámetros que conforman el variograma, es decir, nugget, sill y range:
vm <- vgm(model="Sph",
psill=0.12,
range=850,
nugget=0.01)
plot(ve, pl=T, model=vm, pch=20, xlab = "distance", ylab = "semivariance")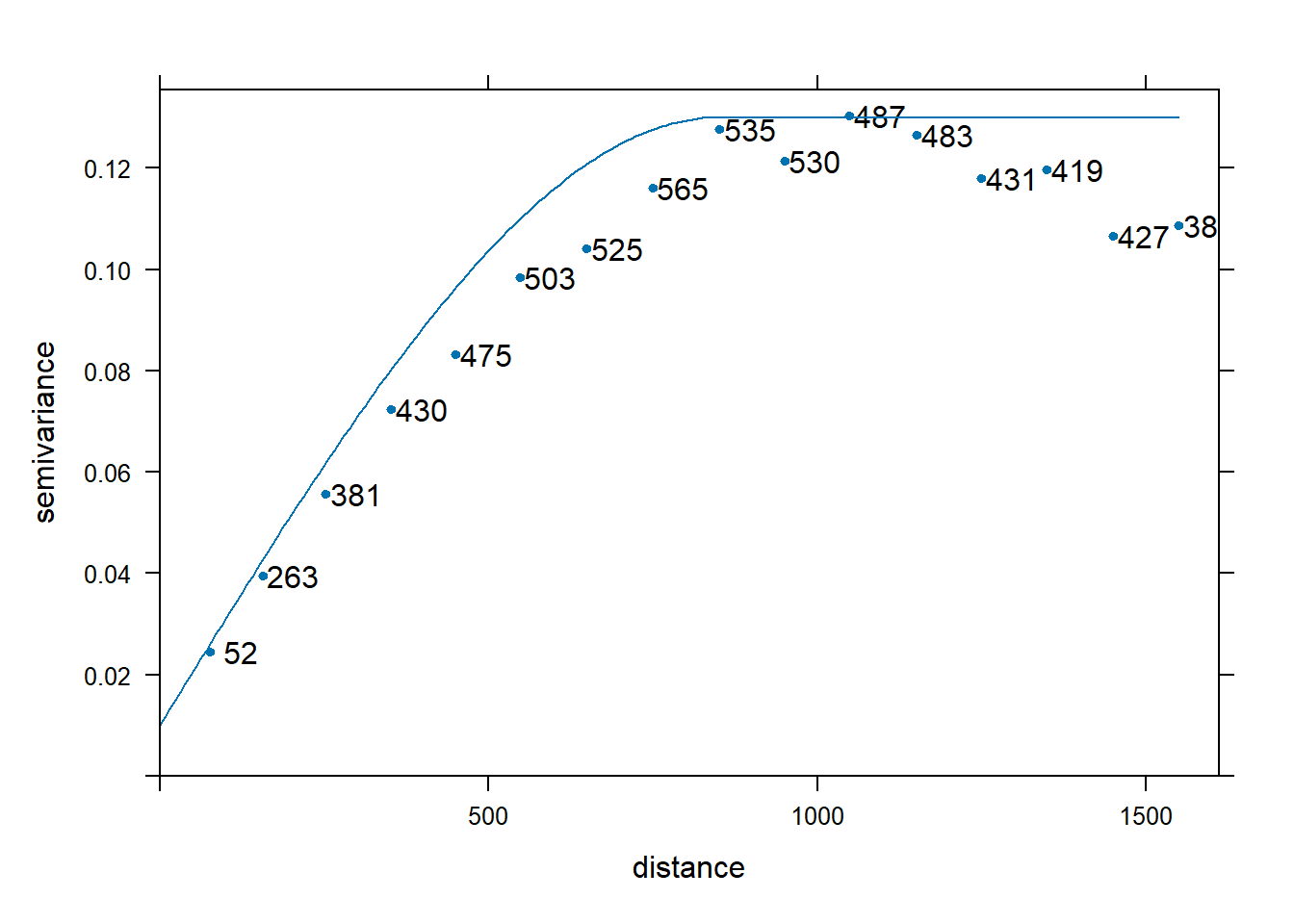
Pero puede que no veamos de forma clara los valores, o no hayamos detectado bien el modelo del variograma teórico… Esto mismo lo podemos hacer de forma automática:
(vmf <- fit.variogram(ve, vm)) model psill range
1 Nug 0.01153321 0.0000
2 Sph 0.11054666 933.3998plot(ve, pl=T, model=vmf, pch=20, xlab = "distance", ylab = "semivariance")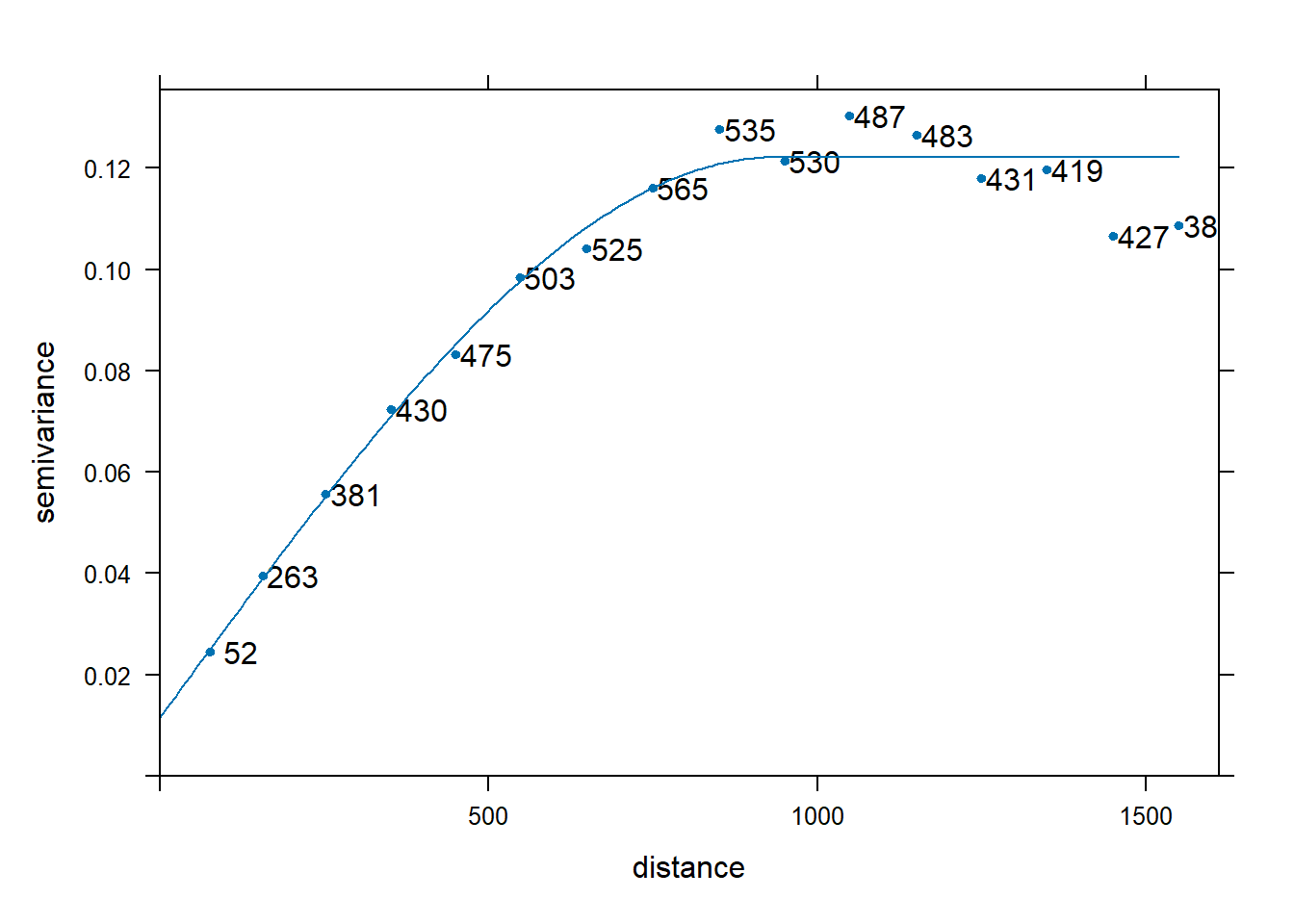
Podemos afirmar, por tanto, que nuestro conjunto de datos sigue un modelo esférico. En realidad, da igual qué modelo se siga, pero esto justifica la existencia de relación entre pares de puntos (a partir de una distancia de 900 metros no existe dependencia).
14.6 Interpolación
Ahora vamos a practicar la interpolación espacial, es decir, calcular valores desconocidos a partir de una muestra. El resultado que vamos a obtener se conoce habitualmente por superficie estadística, una superficie “continua” (capa raster) con valores interpolados a partir de otros conocidos.
14.6.1 Interpolación IDW
Existen muchos métodos de interpolación, como vimos en la sesión de teoría. La interpolación mediante distancia inversa ponderada (IDW) determina los valores desconocidos a partir de una combinación ponderada de un conjunto de puntos de muestra. Este método presupone que el valor de la variable observada disminuye conforme aumenta la distancia respecto del punto muestreado.
Veamos la superficie estadística generada con este método en el caso que nos ocupa (niveles de Zinc en el río Mosa):
data(meuse.grid, package="sp") # obtenemos la malla de celdas de la zona objeto de estudio
class(meuse.grid)[1] "data.frame"names(meuse.grid)[1] "x" "y" "part.a" "part.b" "dist" "soil" "ffreq" meuse.grid.sf <- st_as_sf(meuse.grid, coords = c("x", "y"))
st_crs(meuse.grid.sf) <- st_crs(meuse.sf) #mismo CRS que antes
ggplot(meuse.grid.sf) +
geom_sf() +
theme_classic()
idw <- idw(formula = logZn ~ 1,
locations = meuse.sf,
newdata = meuse.grid.sf)[inverse distance weighted interpolation]head(idw)Simple feature collection with 6 features and 2 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 181100 ymin: 333660 xmax: 181220 ymax: 333740
Projected CRS: Amersfoort / RD New
var1.pred var1.var geometry
1 2.717386 NA POINT (181180 333740)
2 2.779092 NA POINT (181140 333700)
3 2.736429 NA POINT (181180 333700)
4 2.698418 NA POINT (181220 333700)
5 2.886857 NA POINT (181100 333660)
6 2.815193 NA POINT (181140 333660)plot(idw["var1.pred"], pch = 15, nbreaks = 64, pal = bpy.colors, main="IDW")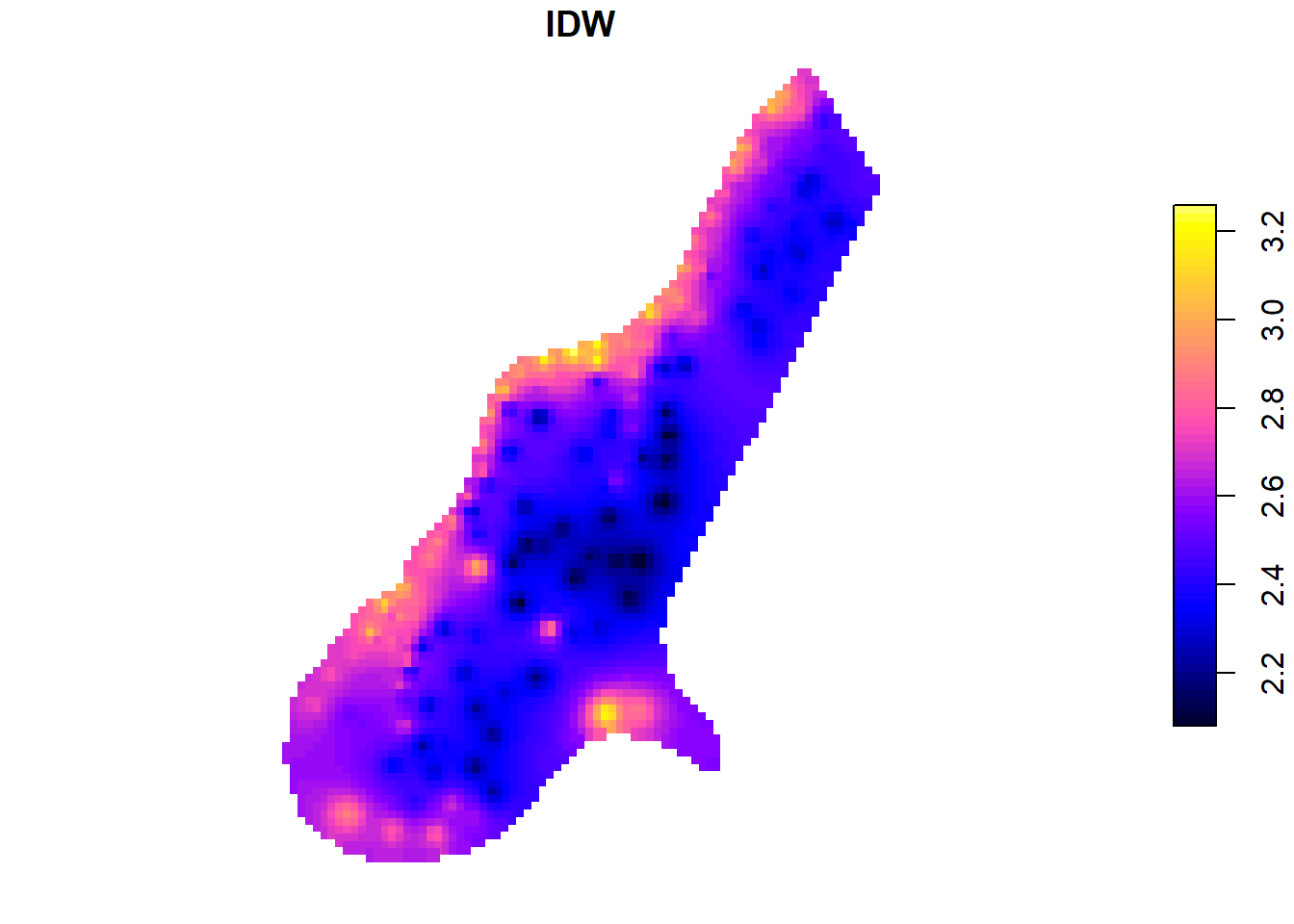
14.6.2 Kriging ordinario
Otro método de interpolación muy utilizado es el kriging ordinario (ordinary kriging). La principal ventaja que tiene este método respecto al anterior es que los pesos asignados a cada valor de la muestra son los óptimos, teniendo en cuenta el variograma (IDW solo tiene en cuenta la distancia).
ok <- krige(formula = logZn ~ 1,
locations = meuse.sf,
newdata = meuse.grid.sf,
model = vmf)[using ordinary kriging]head(ok)Simple feature collection with 6 features and 2 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 181100 ymin: 333660 xmax: 181220 ymax: 333740
Projected CRS: Amersfoort / RD New
var1.pred var1.var geometry
1 2.825653 0.06100097 POINT (181180 333740)
2 2.876953 0.04876651 POINT (181140 333700)
3 2.827099 0.05248213 POINT (181180 333700)
4 2.777134 0.05652607 POINT (181220 333700)
5 2.935171 0.03549881 POINT (181100 333660)
6 2.880816 0.03973172 POINT (181140 333660)plot(ok["var1.pred"],
pch = 15,
nbreaks = 64,
pal = bpy.colors,
main = "Kriging Ordinario")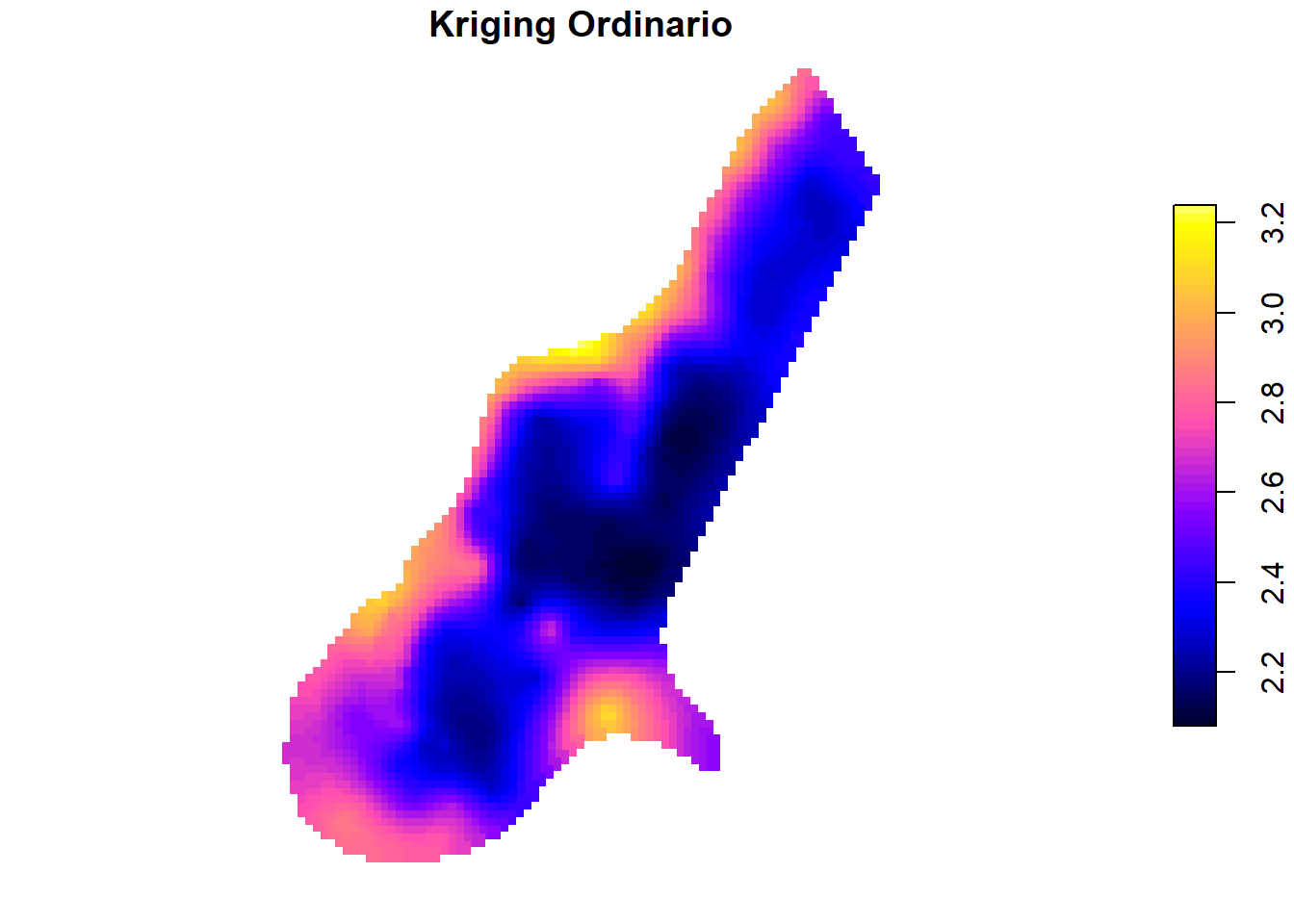
Observando el gráfico podemos afirmar que las zonas con mayores concentraciones de Zinc están claramente identificadas, en las proximidades de la orilla del río.
En este caso, también podemos representar las predicciones de las varianzas:
plot(ok["var1.var"],
pch = 15,
nbreaks = 64,
pal = cm.colors,
main = "Kriging Ordinario - Predicción de la Varianza")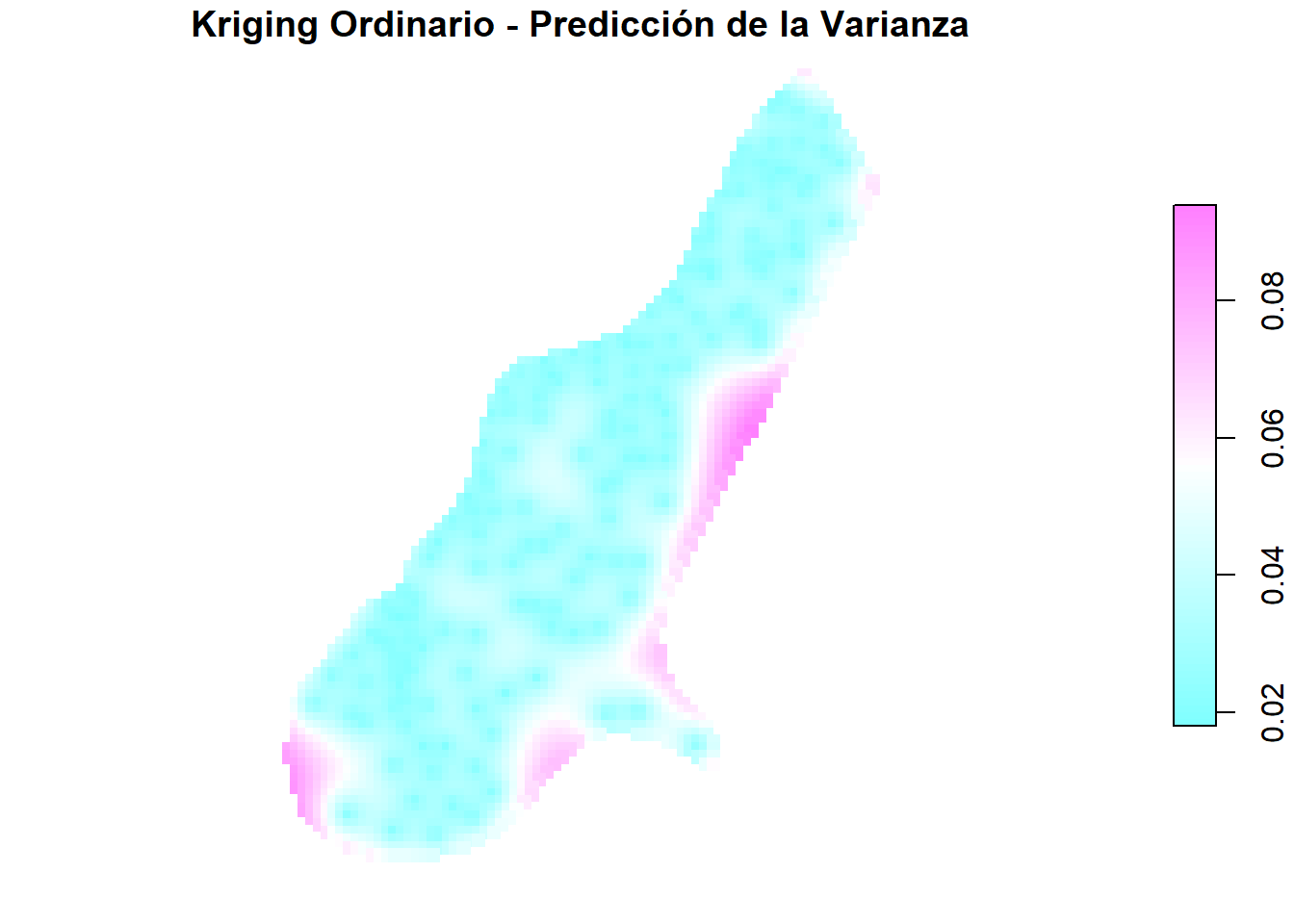
Como se puede observar, las predicciones de las varianzas son bajas en los puntos de observación, pero aún más bajas en la orilla del río, donde se han tomado más muestras. No se observa relación con el valor de la variable ni con la predicción.
Puede ser útil visualizar las predicciones y las observaciones en un mismo gráfico. Para ello usaremos en el plot() el argumento reset = FALSE:
plot(ok["var1.pred"],
pch = 15,
nbreaks = 64,
pal = bpy.colors,
main="Kriging Ordinario + Zinc(ppm)",
reset = FALSE)
plot(meuse.sf["logZn"], add = TRUE,
pch = 1,
col = "white",
cex=4*meuse.sf$zinc/max(meuse.sf$zinc))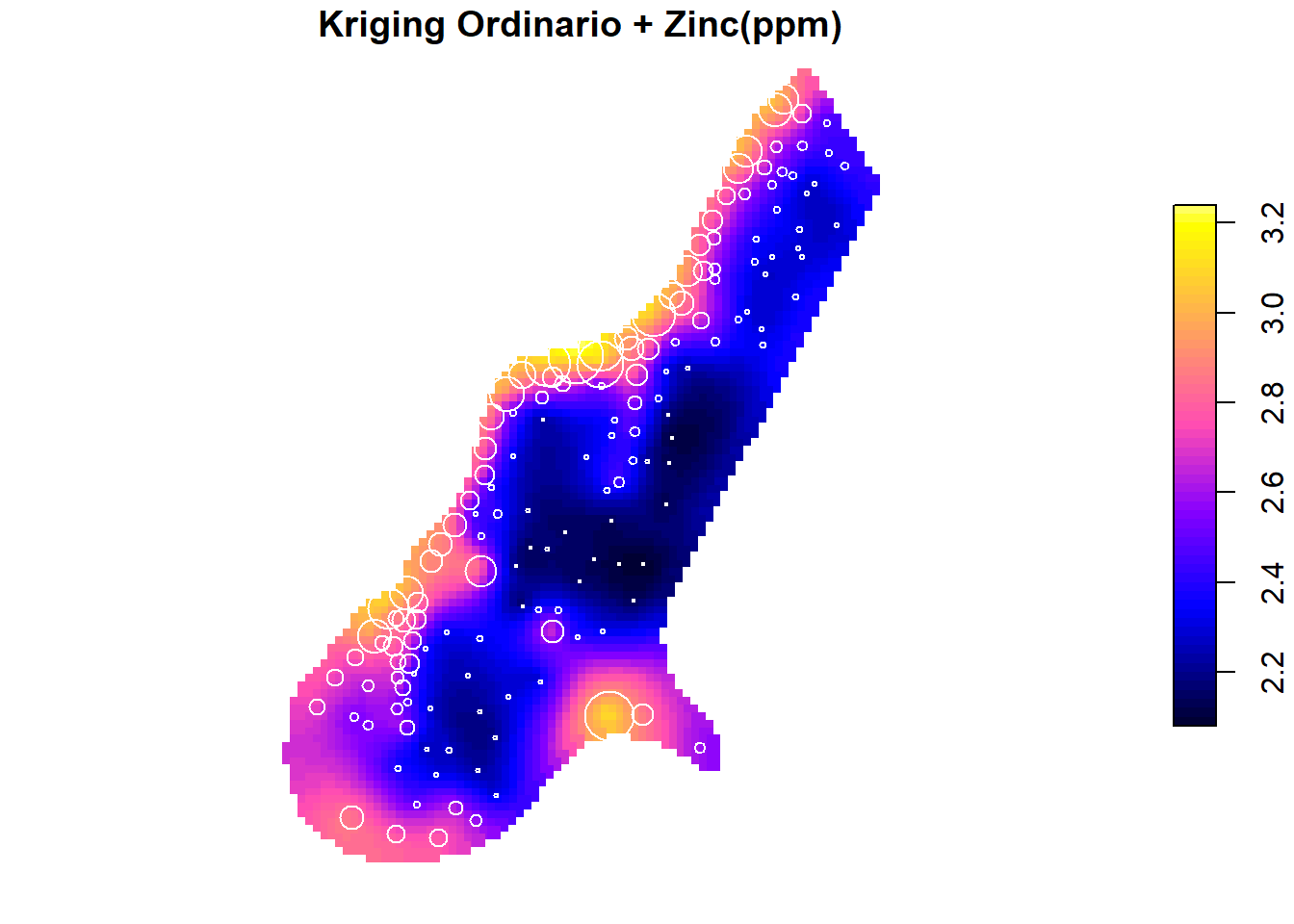
Nota: los valores que puede tomar el argumento pch en un plot() están aquí.
En el caso del gráfico de las varianzas (predicciones), podemos agregar las ubicaciones de las observaciones:
plot(ok["var1.var"],
pch = 15,
nbreaks = 64,
pal = cm.colors,
main="Kriging Ordinario - Predicción de la Varianza",
reset = FALSE)
plot(meuse.sf["logZn"],
add = TRUE,
pch = 20,
col = "darkgray")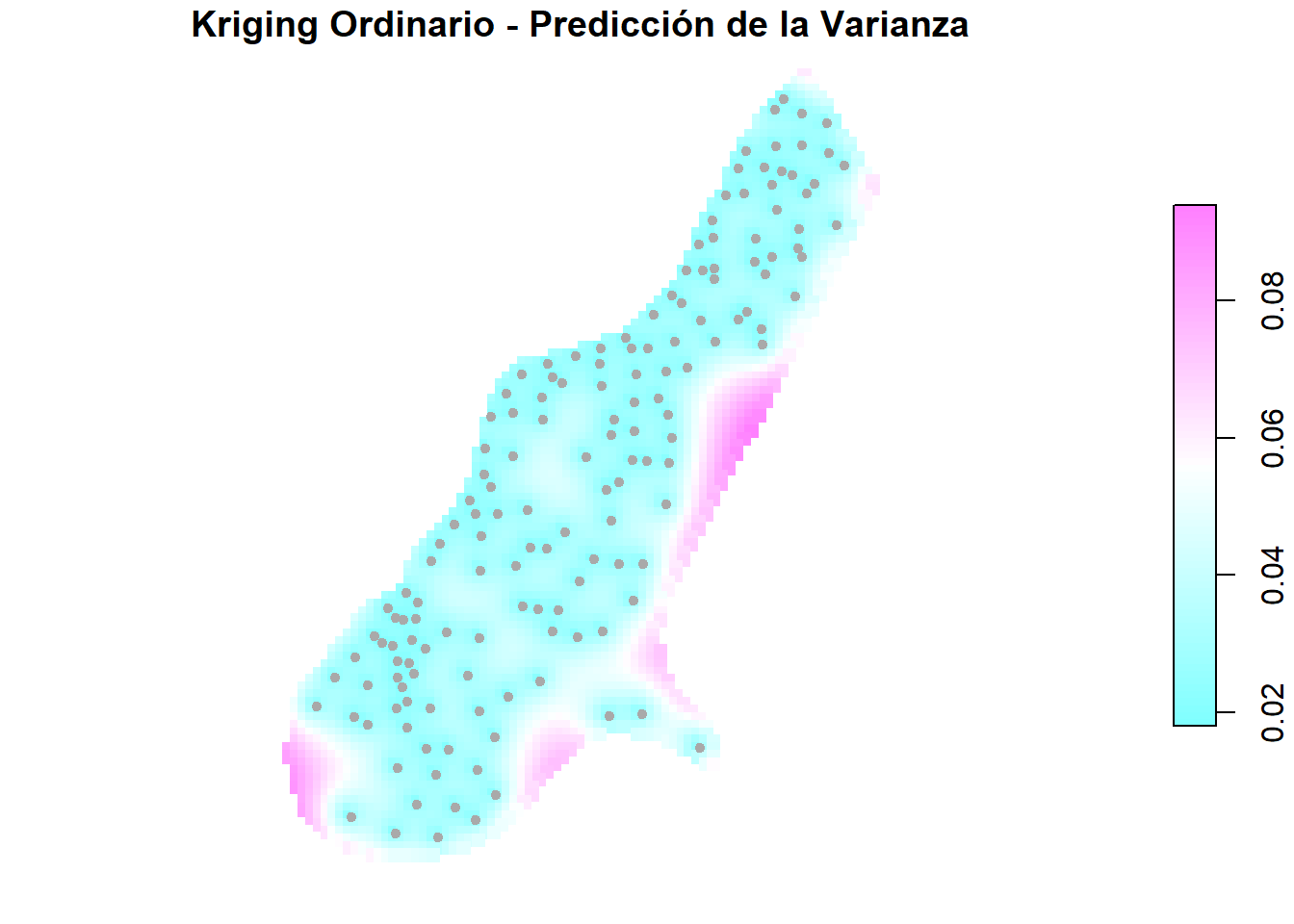
14.7 Validación cruzada
Otra de las características del método kriging es que permite usar el mismo conjunto de datos tanto para modelar y predecir como para evaluar dichas predicciones. Esto se llama validación cruzada. Consiste en predecir los valores en las localizaciones observadas a partir de los datos generados anteriormente. De este modo podemos comparar las predicciones con la realidad. Esta técnica la podemos aplicar también a otro tipo de interpolaciones, como la IDW, mediante la función krige.cv() del paquete gstat(Pebesma y Graeler, 2022):
idw.cv <- krige.cv(formula = log10(zinc) ~ 1, locations = meuse.sf)
head(idw.cv)Simple feature collection with 6 features and 6 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 181025 ymin: 333260 xmax: 181390 ymax: 333611
Projected CRS: Amersfoort / RD New
var1.pred var1.var observed residual zscore fold
1 2.830957 NA 3.009451 0.17849407 NA 1
2 2.797944 NA 3.057286 0.25934204 NA 2
3 2.687633 NA 2.806180 0.11854729 NA 3
4 2.605734 NA 2.409933 -0.19580090 NA 4
5 2.505657 NA 2.429752 -0.07590500 NA 5
6 2.475493 NA 2.448706 -0.02678701 NA 6
geometry
1 POINT (181072 333611)
2 POINT (181025 333558)
3 POINT (181165 333537)
4 POINT (181298 333484)
5 POINT (181307 333330)
6 POINT (181390 333260)ok.cv <- krige.cv(formula = log10(zinc) ~ 1, locations = meuse.sf, model = vmf)
head(ok.cv)Simple feature collection with 6 features and 6 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 181025 ymin: 333260 xmax: 181390 ymax: 333611
Projected CRS: Amersfoort / RD New
var1.pred var1.var observed residual zscore fold
1 2.933377 0.03608242 3.009451 0.076074277 0.40048846 1
2 2.933496 0.03494334 3.057286 0.123789515 0.66221899 2
3 2.735701 0.03592517 2.806180 0.070479172 0.37184452 3
4 2.625683 0.04439572 2.409933 -0.215749965 -1.02395343 4
5 2.426861 0.03460143 2.429752 0.002891681 0.01554545 5
6 2.358252 0.04507897 2.448706 0.090454692 0.42603386 6
geometry
1 POINT (181072 333611)
2 POINT (181025 333558)
3 POINT (181165 333537)
4 POINT (181298 333484)
5 POINT (181307 333330)
6 POINT (181390 333260)Comparamos las predicciones con los datos reales, para los dos tipos de interpolación:
par(mfrow=c(1,2))
plot(var1.pred~observed, idw.cv, pch = 20, main="IDW", reset = FALSE)
plot(var1.pred~observed, ok.cv, pch = 20, main="Ordinary Kriging")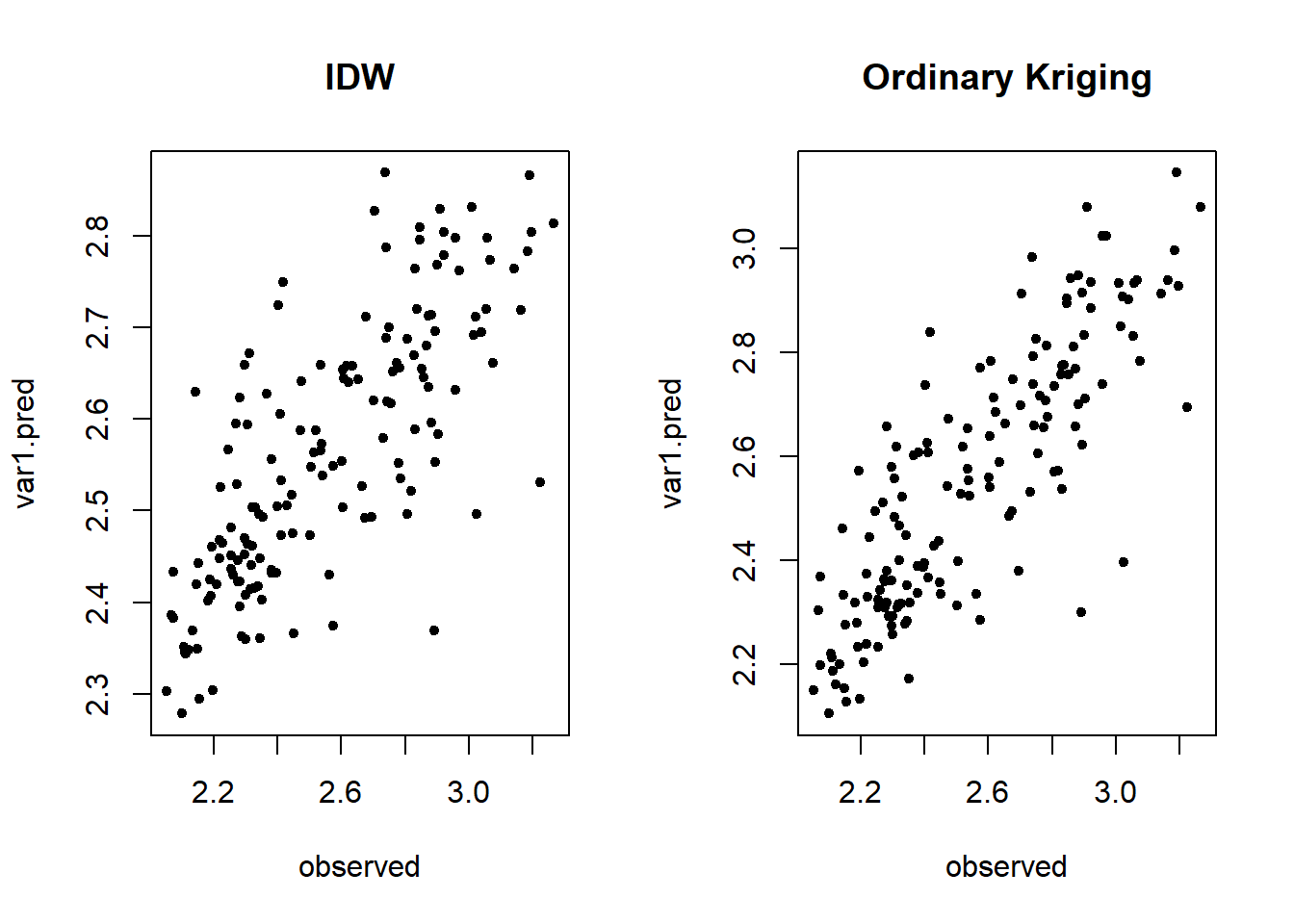
Da la sensación que en el gráfico de la derecha los puntos están más agrupados, ¿no? Vamos a comprobarlo…
Podemos calcular el coeficiente de correlación entre valores reales y predicciones (1 equivale a relación perfecta):
(cor.idw.cv <- cor(idw.cv$var1.pred, idw.cv$observed))[1] 0.7640391(cor.ok.cv <- cor(ok.cv$var1.pred, ok.cv$observed))[1] 0.8357297Y también podemos calcular el error de la interpolación (la media de los residuos). Cuanto más pequeño, mejor:
(mean.idw.resid <- mean(idw.cv$residual))[1] -0.005565866(mean.ok.resid <- mean(ok.cv$residual))[1] -0.0001333146Y también podemos calcular el error cuadrático medio (RMSE):
(rmse.idw <- sqrt(sum(idw.cv$residual^2)/length(idw.cv$residual)))[1] 0.2231549(rmse.ok <- sqrt(sum(ok.cv$residual^2)/length(ok.cv$residual)))[1] 0.1718811