library(terra)
library(sf)
train_points <- sf::read_sf("https://www.uv.es/dataenhance/DEE/temp_train.gpkg")
predictor_stack <- terra::rast("https://www.uv.es/dataenhance/DEE/predictors.tif")17 Spatial Machine Learning
17.1 Introducción
El lenguaje R cuenta con una amplia variedad de paquetes para aprendizaje automático (machine learning o ML), y muchas de las librerías pueden utilizarse/aplicarse en contextos espaciales, lo que da lugar al denominado aprendizaje automático espacial (spatial machine learning o SML). Recordemos el flujo de trabajo de una tarea de aprendizaje automático:
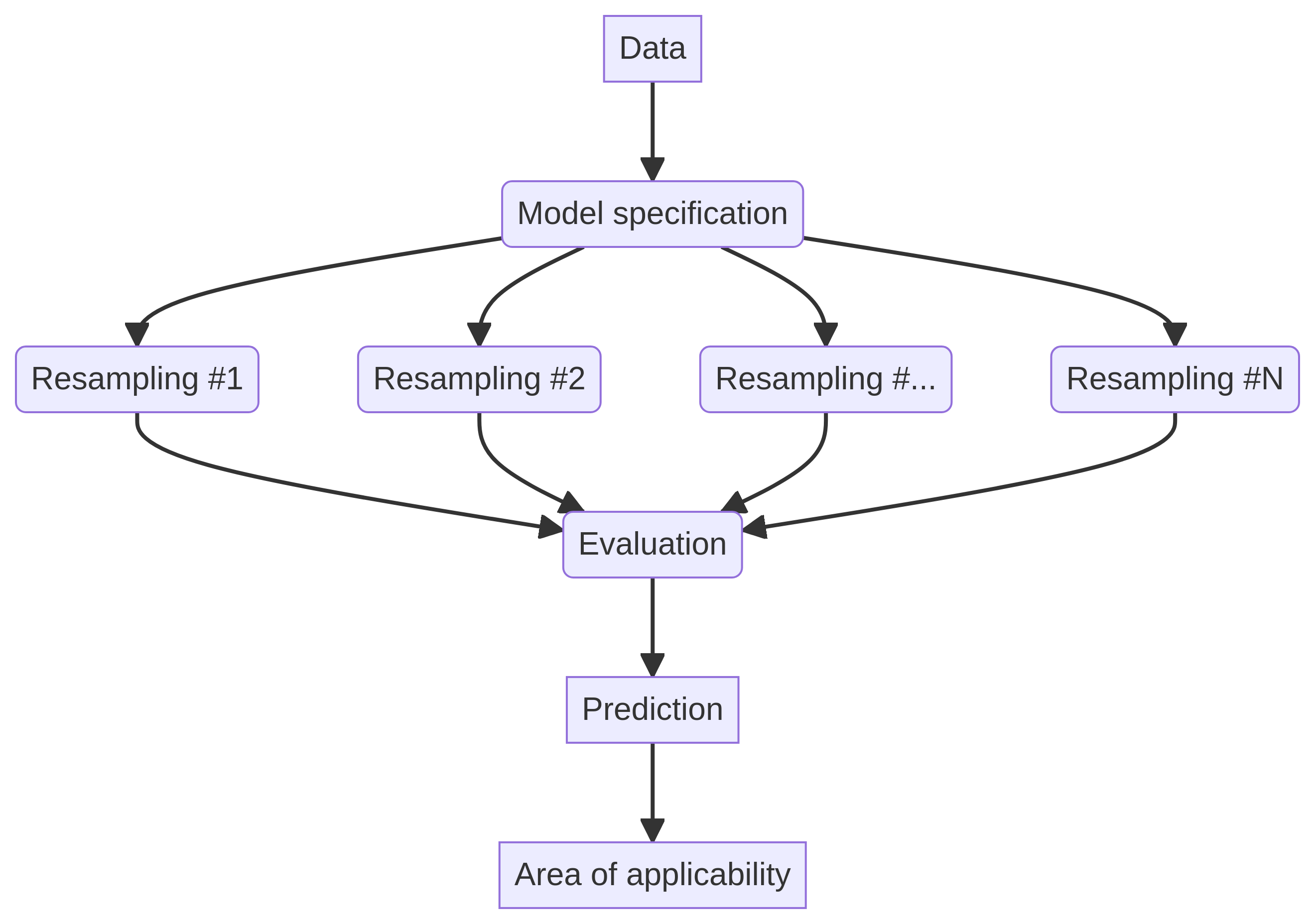
El SML se diferencia del ML tradicional en que incorpora explícitamente la dependencia espacial: como vimos en sesiones anteriores, las observaciones geográficamente cercanas tienden a ser más similares entre sí que aquellas ubicadas a mayor distancia, en línea con la primera ley de la geografía de Tobler. Esta dependencia espacial debe ser tenida en cuenta al construir modelos de ML que trabajen con datos geográficos, ya que puede influir en la validez y generalización de los resultados. Ignorarla podría llevar a interpretaciones erróneas o a modelos que no capturen adecuadamente los patrones espaciales subyacentes.
En esta práctica, exploraremos tres de los marcos de trabajo más populares para ML en R: caret(Kuhn, 2022; Kuhn y Max, 2008), tidymodels(Kuhn y Wickham, 2025) y mlr3(Lang et al., 2019; Lang et al., 2025). Utilizaremos un ejemplo sencillo para ilustrar cómo aplicar estos paquetes a una tarea de aprendizaje automático espacial, destacando las diferencias en sus flujos de trabajo, enfoques y sintaxis. El objetivo es brindar una visión general de estas herramientas, sentando las bases para que cada estudiante pueda profundizar en la que mejor se adapte a sus necesidades analíticas o intereses de investigación.
17.2 Datos
En esta sesión vamos a tratar de predecir la temperatura en España utilizando un conjunto de covariables. Para ello, contamos con dos conjuntos de datos: el primero, temperature_train, contiene las mediciones de temperatura de 195 ubicaciones en España; el segundo, predictor_stack, incluye las covariables que usaremos para predecir la temperatura. Estas covariables incluyen variables como la densidad de población (popdens), la distancia a la costa (coast) y la altitud (elev), entre otras.
Usaremos un subconjunto de catorce covariables para predecir la temperatura, pero antes, y para preparar los datos para el modelado, necesitamos extraer los valores de las covariables en las ubicaciones de nuestros puntos de entrenamiento:
predictor_names <- names(predictor_stack)[1:14]
temperature_train <- terra::extract(
predictor_stack[[predictor_names]],
train_points,
bind = TRUE
) %>%
sf::st_as_sf()
dplyr::glimpse(temperature_train)Rows: 195
Columns: 16
$ temp <dbl> 17.52610, 16.94795, 17.49233, 15.30838, 16.56…
$ popdens <dbl> 0.000000, 1.211701, 5.681698, 4752.076660, 17…
$ coast <dbl> 1.1263009, 6.7432733, 1.7549587, 45.7688789, …
$ dem <dbl> 85.9054031, 75.0012589, 2.5561547, 256.110870…
$ imd <dbl> 27.359106, 16.854668, 83.219482, 40.664047, 1…
$ ntl <dbl> 20.126450, 8.056596, 180.887161, 36.842339, 3…
$ ndvi <dbl> 0.3656146, 0.3990190, 0.1987631, 0.3861388, 0…
$ primaryroads <dbl> 4.6346059, 0.0000000, 3.2220817, 2.1847610, 1…
$ otherroads <dbl> 3.773046, 2.709918, 10.960647, 10.480736, 7.8…
$ urban <dbl> 0.00000000, 0.00000000, 0.00000000, 0.4981314…
$ industry <dbl> 0.2819442, 0.3051900, 0.9983283, 0.1316080, 0…
$ agriculture <dbl> 0.000000000, 0.694810033, 0.000000000, 0.0011…
$ natural <dbl> 0.718055785, 0.000000000, 0.001671706, 0.3691…
$ CAMSpm25 <dbl> 8.077613, 9.175149, 13.225924, 11.543165, 15.…
$ lst_day <dbl> 24.37792, 28.13341, 25.76198, 26.97013, 22.47…
$ geometry <POINT [m]> POINT (825940.4 4541533), POINT (849548…17.3 Librerías
Cargamos las librerías necesarias:
library(caret) # modelado
library(blockCV) # validación cruzada espacial
library(CAST) # área de aplicabilidad (AoA)library(tidymodels) # metapackage para modelado
library(spatialsample) # validación cruzada espacial
library(waywiser) # área de aplicabilidad (AoA)
library(vip) # importancia de variable (se usa en AoA)library(mlr3verse) # metapackage para modelado
library(mlr3spatiotempcv) # validación cruzada espacial
library(CAST) # área de aplicabilidad (AoA)17.4 Especificaciones del modelo
Cada uno de los tres marcos de trabajo (frameworks) que veremos en esta sesión tiene su propia forma de configurar el flujo de trabajo de modelado (modeling workflow), teniendo que definir, entre otros, el modelo, el método de remuestreo y los valores de los hiperparámetros. En este ejemplo, utilizaremos modelos de bosque aleatorio (random forest) implementados en el paquete ranger(Wright et al., 2024; Wright y Ziegler, 2017), con los siguientes hiperparámetros:
- mtry: número de variables seleccionadas aleatoriamente como candidatas en cada división, con un valor de 8.
- splitrule: regla de partición, configurada como “extratrees”.
- min.node.size: tamaño mínimo de los nodos terminales, con un valor de 5.
También emplearemos un método de validación cruzada espacial (spatial cross-validation) con 5 particiones (folds). Esto significa que los datos se dividen en varios bloques espaciales, y cada bloque se asigna a una partición. El modelo se entrena con los bloques asignados al conjunto de entrenamiento y se evalúa con los bloques restantes. Cabe destacar que cada marco de trabajo define el método de remuestreo de forma diferente, por lo que la implementación y las particiones pueden variar ligeramente entre ellos.
Para caret(Kuhn, 2022), definimos la matriz de hiperparámetros (hyperparameter grid) utilizando la función expand.grid(), y el método de remuestreo con la función trainControl(). En este caso, para aplicar validación cruzada espacial, utilizamos el paquete blockCV(Valavi et al., 2019, 2024) para crear las particiones (folds), y luego las pasamos a la función trainControl().
set.seed(semilla)
tn_grid <- expand.grid(
mtry = 8,
splitrule = "extratrees",
min.node.size = 5
)
spatial_blocks <- blockCV::cv_spatial(
temperature_train,
k = 5,
hexagon = FALSE,
progress = FALSE
)
train test
1 155 40
2 158 37
3 158 37
4 155 40
5 154 41
train_ids <- lapply(spatial_blocks$folds_list, function(x) x[[1]])
test_ids <- lapply(spatial_blocks$folds_list, function(x) x[[2]])
tr_control <- caret::trainControl(
method = "cv",
index = train_ids,
indexOut = test_ids,
savePredictions = TRUE
)En tidymodels(Kuhn y Wickham, 2025), los pasos son los siguientes:
- Especificar la fórmula del modelo utilizando la función
recipe(). - Definir el modelo con una función del paquete
parsnip(Kuhn y Vaughan, 2025), incluyendo los hiperparámetros. - Crear un flujo de trabajo con la función
workflow(), que combina la fórmula y el modelo. - Definir el método de remuestreo usando la función
spatial_block_cv()del paquetespatialsample(Mahoney y Silge, 2024).
set.seed(semilla)
form <- as.formula(paste0("temp ~ ", paste(predictor_names, collapse = " + ")))
recipe <- recipes::recipe(form, data = temperature_train)
rf_model <- parsnip::rand_forest(
trees = 100,
mtry = 8,
min_n = 5,
mode = "regression"
) %>%
parsnip::set_engine("ranger", splitrule = "extratrees", importance = "impurity")
workflow <- workflows::workflow() %>%
workflows::add_recipe(recipe) %>%
workflows::add_model(rf_model)
block_folds <- spatialsample::spatial_block_cv(temperature_train, v = 5)
spatialsample::autoplot(block_folds)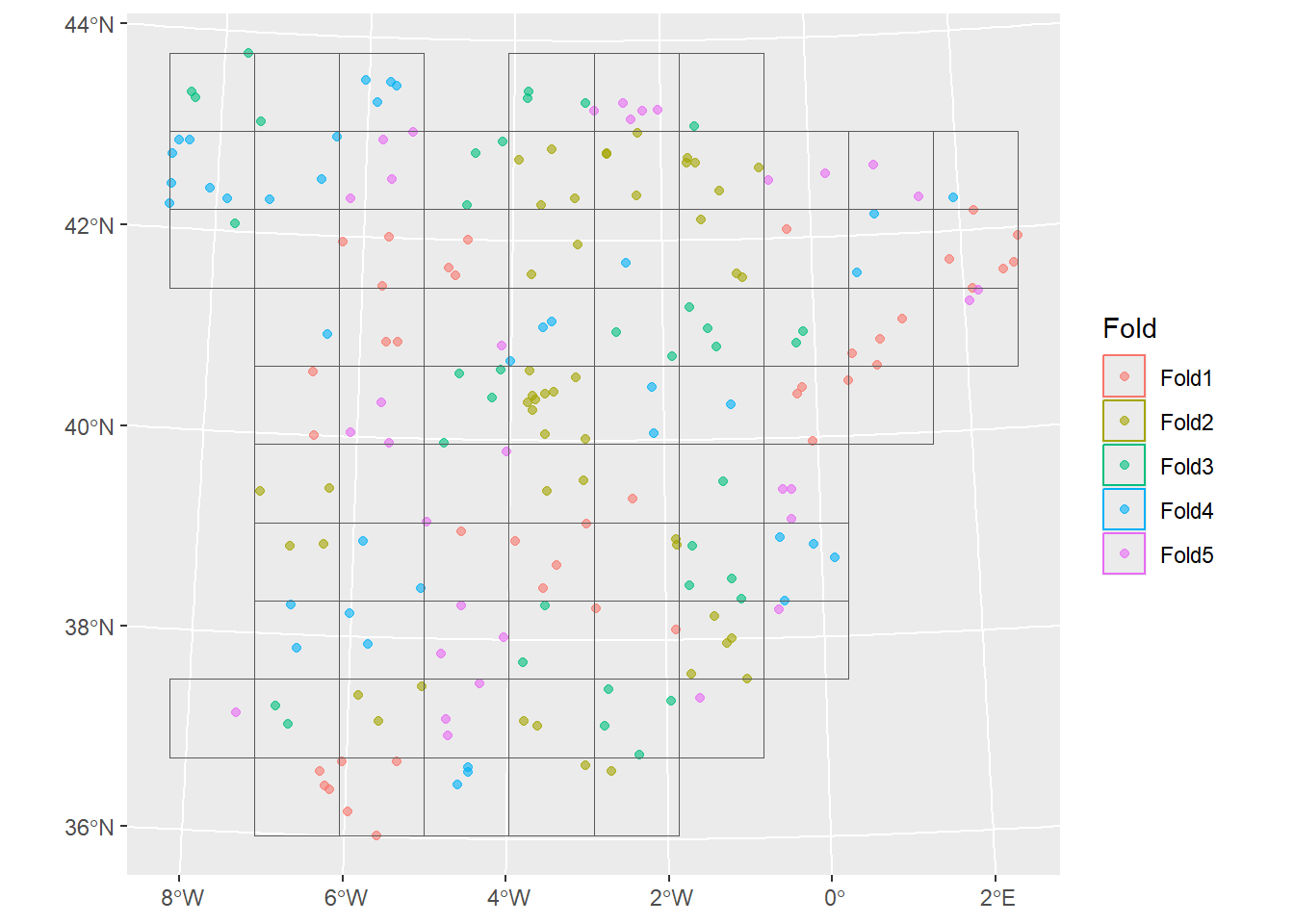
Los tres pasos básicos en mlr3(Lang et al., 2025) son estos:
- Task: se define utilizando la función
as_task_regr_st(), donde se especifica la variable objetivo y los datos a utilizar.
- Learner: se define el modelo mediante la función
lrn(), donde se indica el tipo de modelo y los hiperparámetros.
- Resampling: se define el método de remuestreo con la función
rsmp(), especificando el tipo de remuestreo y el número de particiones (folds). En este caso, utilizamos el método de remuestreo “spcv_block”.
set.seed(semilla)
task <- mlr3spatiotempcv::as_task_regr_st(temperature_train, target = "temp")
learner <- mlr3::lrn("regr.ranger",
num.trees = 100,
importance = "impurity",
mtry = 8,
min.node.size = 5,
splitrule = "extratrees"
)
resampling <- mlr3::rsmp("spcv_block", folds = 5, cols = 10, rows = 10)17.5 Modelado
La función principal del paquete caret es train(), la cual recibe como argumentos la fórmula del modelo, los datos, el tipo de modelo, la cuadrícula de ajuste (tuning grid), el control de entrenamiento (que incluye el método de remuestreo), y algunos otros parámetros (por ejemplo, el número de árboles). La función train() realiza automáticamente el remuestreo y el ajuste de hiperparámetros (si corresponde). El modelo final entrenado se almacena en el objeto finalModel.
model_caret <- caret::train(
temp ~ .,
data = st_drop_geometry(temperature_train),
method = "ranger",
tuneGrid = tn_grid,
trControl = tr_control,
num.trees = 100,
importance = "impurity"
)
model_caret_final <- model_caret$finalModelEn tidymodels, la función fit_resamples() recibe el flujo de trabajo previamente definido y las particiones de remuestreo. En este caso, también utilizamos el argumento control para guardar las predicciones y el flujo de trabajo, lo cual puede ser útil para análisis posteriores. La función fit_best() se emplea para ajustar el mejor modelo según los resultados del remuestreo.
rf_spatial <- tune::fit_resamples(
workflow,
resamples = block_folds,
control = tune::control_resamples(save_pred = TRUE, save_workflow = TRUE)
)Warning: package 'ranger' was built under R version 4.4.3model_tidymodels <- fit_best(rf_spatial)El flujo de trabajo en mlr3 aplica la función resample() a la tarea (task), al modelo (learner) y al método de remuestreo. Luego, para obtener el modelo final, se utiliza la función train() con la tarea y el modelo previamente definidos.
model_mlr3 <- mlr3::resample(
task = task,
learner = learner,
resampling = resampling
)Warning: package 'future' was built under R version 4.4.3Warning: package 'mlr3fselect' was built under R version 4.4.3INFO [17:51:14.524] [mlr3] Applying learner 'regr.ranger' on task 'temperature_train' (iter 1/5)
INFO [17:51:14.614] [mlr3] Applying learner 'regr.ranger' on task 'temperature_train' (iter 2/5)
INFO [17:51:14.669] [mlr3] Applying learner 'regr.ranger' on task 'temperature_train' (iter 3/5)
INFO [17:51:14.716] [mlr3] Applying learner 'regr.ranger' on task 'temperature_train' (iter 4/5)
INFO [17:51:14.759] [mlr3] Applying learner 'regr.ranger' on task 'temperature_train' (iter 5/5)learner$train(task)17.6 Evaluación
Una vez entrenados los modelos, queremos evaluar su rendimiento. Para ello, utilizamos dos de las métricas más comunes en tareas de regresión: el error cuadrático medio (\(RMSE\), por sus siglas en inglés) y el coeficiente de determinación \(R^2\).
El error cuadrático medio y el coeficiende de determinación se calculan por defecto en caret. Las métricas de rendimiento se almacenan en el objeto results del modelo.
model_caret$results mtry splitrule min.node.size RMSE Rsquared MAE
1 8 extratrees 5 1.108607 0.8664234 0.8809489
RMSESD RsquaredSD MAESD
1 0.1278955 0.03806046 0.09205022El error cuadrático medio y el coeficiende de determinación se calculan por defecto en tidymodels. Las métricas de rendimiento se extraen de los resultados del remuestreo utilizando la función collect_metrics().
tune::collect_metrics(rf_spatial)# A tibble: 2 × 6
.metric .estimator mean n std_err .config
<chr> <chr> <dbl> <int> <dbl> <chr>
1 rmse standard 1.16 5 0.0666 Preprocessor1_Model1
2 rsq standard 0.848 5 0.0210 Preprocessor1_Model1En mlr3 necesitamos especificar las métricas que queremos calcular utilizando la función msr(). Luego, el método aggregate() se utiliza para calcular las métricas de desempeño seleccionadas.
my_measures <- c(mlr3::msr("regr.rmse"), mlr3::msr("regr.rsq"))
model_mlr3$aggregate(measures = my_measures)regr.rmse rsq
1.1137802 0.8327327 17.7 Predicción
Nuestro objetivo es predecir la temperatura en España utilizando las covariables del conjunto de datos predictor_stack. Por lo tanto, queremos obtener un mapa con los valores de temperatura predichos para todo el país. La función predict() del paquete terra(Hijmans, 2025) permite realizar predicciones del modelo sobre los nuevos datos ráster.
pred_caret <- terra::predict(predictor_stack, model_caret, na.rm = TRUE)
plot(pred_caret)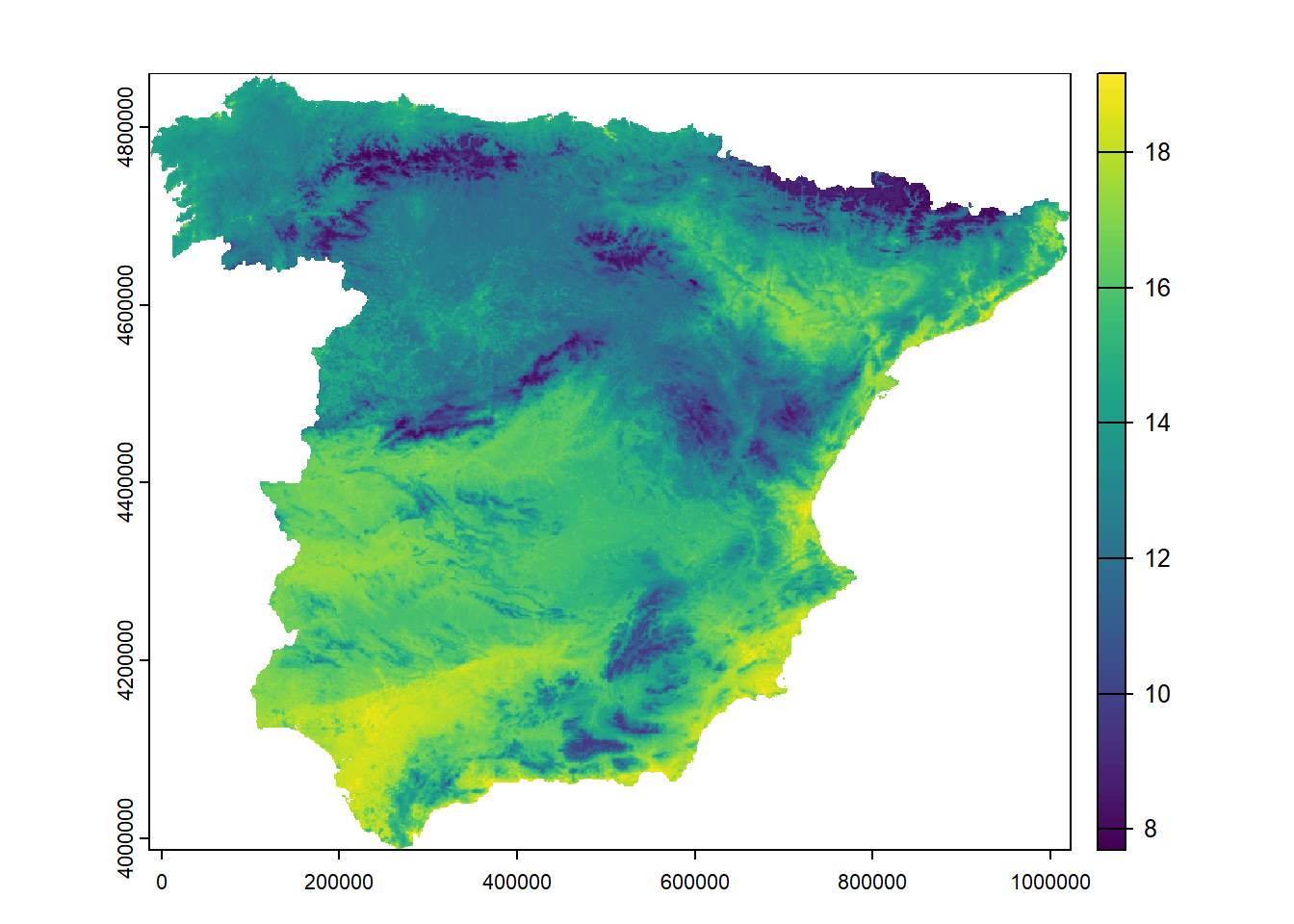
pred_tidymodels <- terra::predict(predictor_stack, model_tidymodels, na.rm = TRUE)
plot(pred_tidymodels)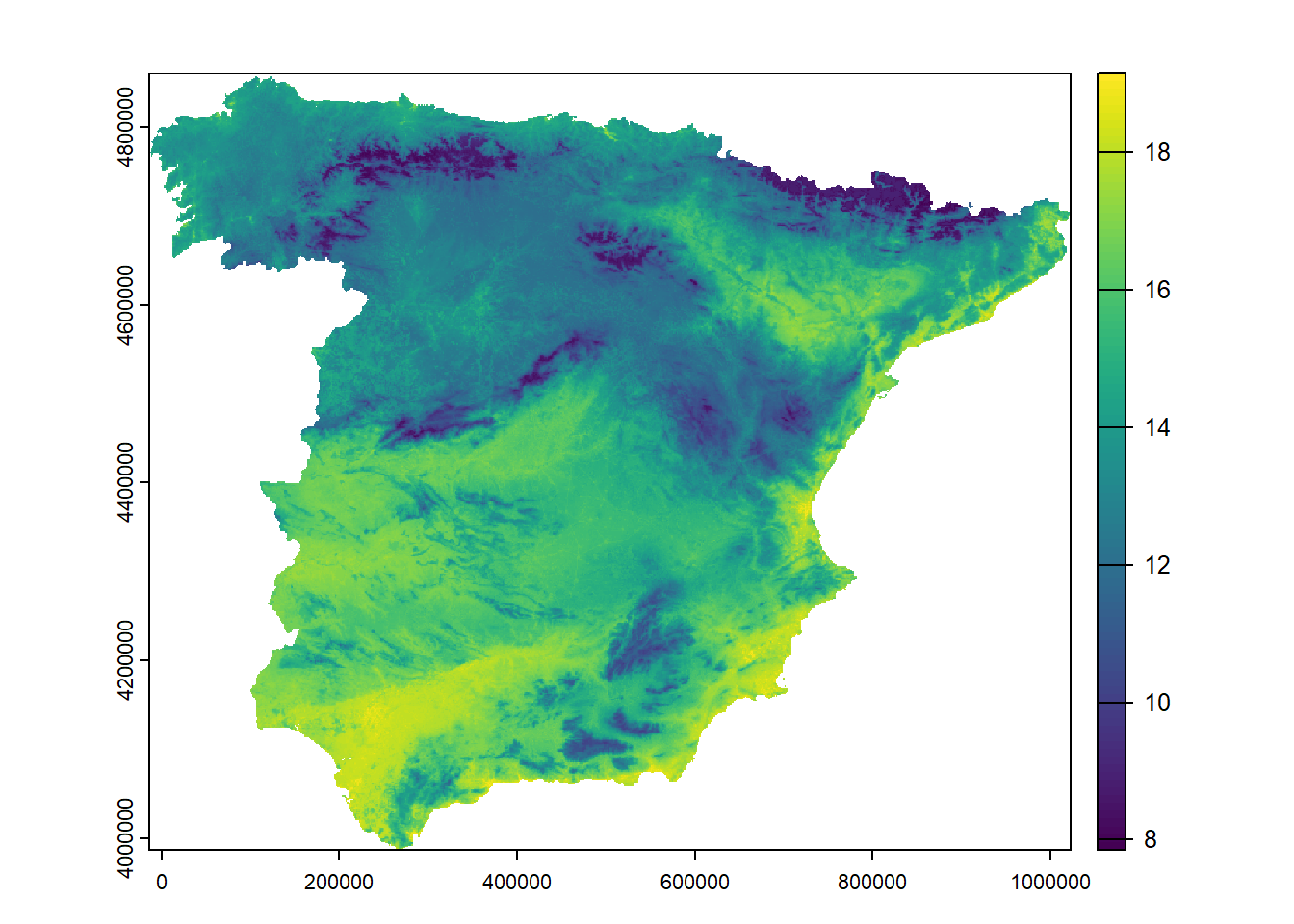
pred_mlr3 <- terra::predict(predictor_stack, learner, na.rm = TRUE)
plot(pred_mlr3)
17.8 Área de aplicabilidad
El área de aplicabilidad (Area of Applicability o AoA) es un método que permite evaluar qué parte del espacio de entrada es similar a los datos de entrenamiento. Es muy útil para analizar el rendimiento del modelo e identificar las zonas donde puede aplicarse con mayor fiabilidad. Las áreas que se encuentran fuera del AoA se consideran fuera del dominio de aplicabilidad del modelo, por lo que las predicciones en esas zonas deben interpretarse con precaución o, idealmente, no utilizarse.
La implementación original del método AoA se encuentra en el paquete CAST(Meyer et al., 2025), un paquete que extiende las funcionalidades de caret. El AoA se calcula utilizando la función aoa(), que recibe como entrada los nuevos datos (las covariables) y el modelo entrenado.
AOA_caret <- CAST::aoa(
newdata = predictor_stack,
model = model_caret,
verbose = FALSE
)
plot(AOA_caret$AOA)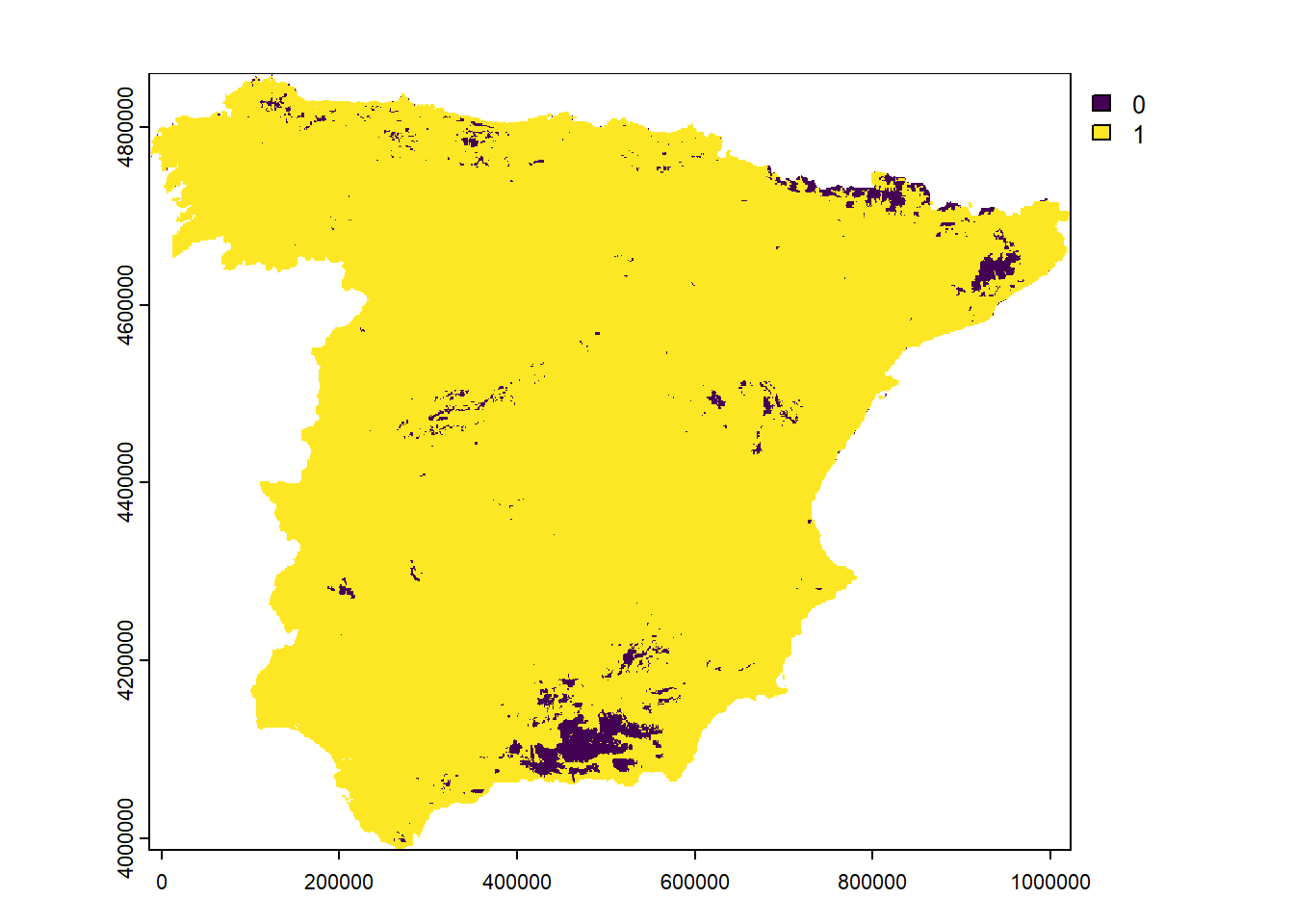
El paquete waywiser(Mahoney, 2025) implementa el método AoA para tidymodels. La función ww_area_of_applicability() recibe como entrada los datos de entrenamiento y la importancia de las variables. Luego, para obtener el AoA sobre los datos espaciales, se utiliza la función predict() del paquete terra.
model_aoa <- waywiser::ww_area_of_applicability(
sf::st_drop_geometry(temperature_train[, predictor_names]),
importance = vip::vi_model(model_tidymodels)
)
AOA_tidymodels <- terra::predict(predictor_stack, model_aoa)
plot(AOA_tidymodels$aoa)
El paquete CAST también puede calcular el AoA para modelos de mlr3. Sin embargo, en este caso es necesario especificar varios argumentos, como un ráster con las covariables, los datos de entrenamiento, las variables a utilizar, los pesos de las variables y las particiones de validación cruzada (folds).
rsmp_cv <- resampling$instantiate(task)
AOA_mlr3 <- CAST::aoa(
newdata = predictor_stack,
train = as.data.frame(task$data()),
variables = task$feature_names,
weight = data.frame(t(learner$importance())),
CVtest = rsmp_cv$instance[order(row_id)]$fold,
verbose = FALSE
)
plot(AOA_mlr3$AOA)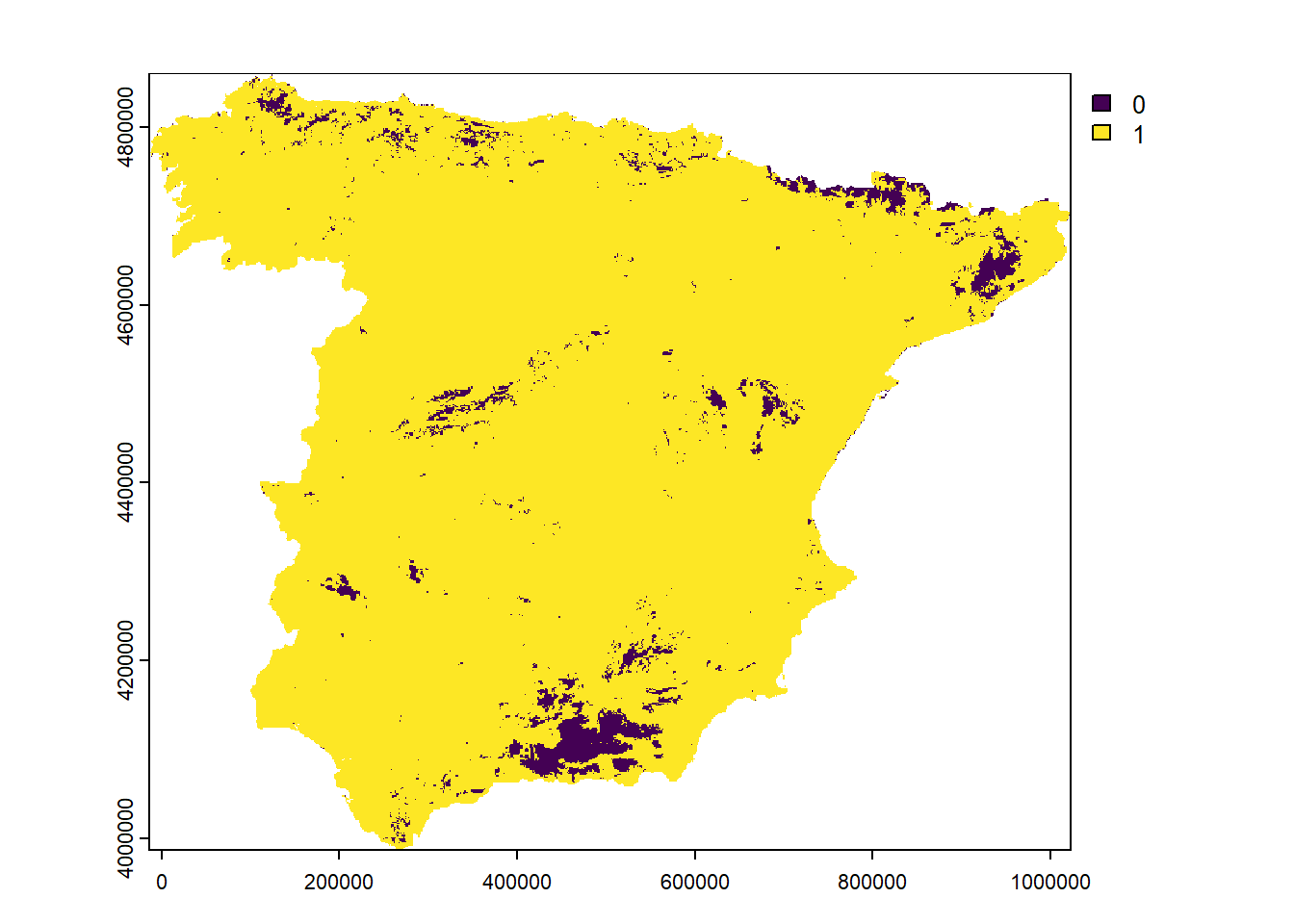
17.9 Conclusión
En esta práctica, se establece una comparativa entre tres de los frameworks para ML más populares en R: caret, tidymodels y mlr3. Como hemos visto, existe una gran superposición en la funcionalidad de los tres entornos de trabajo. Sin embargo, difieren en su filosofía de diseño e implementación. Algunos, como caret, están más enfocados en ofrecer una interfaz coherente y concisa, aunque con menor flexibilidad. Otros, como tidymodels y mlr3, son más modulares y flexibles, lo que permite desarrollar flujos de trabajo más complejos y personalizables, pero también implica una mayor curva de aprendizaje.
Muchos otros pasos podrían incorporarse al flujo de trabajo presentado, como la ingeniería de características (feature engineering), la selección de variables, el ajuste de hiperparámetros, la interpretación del modelo, entre otros. Por ello, esta sesión sienta las bases para el desarrollo de procesos más avanzados en SML, proporcionando una visión comparativa que puede ayudar al usuario a elegir el entorno de trabajo más adecuado según sus necesidades, nivel de experiencia y objetivos analíticos.
17.10 Agradecimientos
Esta práctica se ha basado en el trabajo realizado por Jakub Nowosad:
