library(tidyverse)
library(sp)
library(spdep) # necesita spData y sf
library(mapSpain)
library(tmap)
library(rgeoda)
library(RColorBrewer)16 Datos regionales
16.1 Introducción
En esta práctica vamos a practicar el análisis de datos regionales. Para ello utilizaremos un conjunto de datos utilizado en diversas publicaciones científicas tales como Waller y Gotway (2004) o Bivand et al. (2013). Este dataset, formado por 281 observaciones y 12 variables, contiene información sobre la incidencia de leucemia a nivel de sección censal (census tract) que cubren una región de ocho condados del norte del estado de Nueva York (USA).
16.2 Librerías y datos
En esta práctica utilizaremos funciones de las librerías tidyverse(Wickham, 2022), sf(Pebesma, 2022), sp(Pebesma y Bivand, 2023), spData(Bivand et al., 2022), spdep(Bivand, 2022), mapSpain(Hernangómez, 2025), tmap(Tennekes, 2018), rgeoda(Xun Li y Luc Anselin, 2024) y RColorBrewer(Neuwirth, 2022). Las instalamos y cargamos:
Obtenemos el dataset con el que vamos a trabajar:
NY <- spData::nydata
class(NY)[1] "data.frame"dim(NY)[1] 281 12head(NY) AREANAME AREAKEY X Y POP8 TRACTCAS
1 Binghamton city 36007000100 4.069397 -67.3533 3540 3.08
2 Binghamton city 36007000200 4.639371 -66.8619 3560 4.08
3 Binghamton city 36007000300 5.709063 -66.9775 3739 1.09
4 Binghamton city 36007000400 7.613831 -65.9958 2784 1.07
5 Binghamton city 36007000500 7.315968 -67.3183 2571 3.06
6 Binghamton city 36007000600 8.558753 -66.9344 2729 1.06
PROPCAS PCTOWNHOME PCTAGE65P Z AVGIDIST PEXPOSURE
1 0.000870 0.3277311 0.1466102 0.14197 0.2373852 3.167099
2 0.001146 0.4268293 0.2351124 0.35555 0.2087413 3.038511
3 0.000292 0.3377396 0.1380048 -0.58165 0.1708548 2.838229
4 0.000384 0.4616048 0.1188937 -0.29634 0.1406045 2.643366
5 0.001190 0.1924370 0.1415791 0.45689 0.1577753 2.758587
6 0.000388 0.3651786 0.1410773 -0.28123 0.1726033 2.848411Para saber los datasets que hay disponibles en el paquete spData ejecutar la siguiente sentencia data(package="spData").
Como vemos, el objeto NY es un data.frame, por lo que, como en otras ocasiones, lo primero que debemos hacer es georreferenciar el dataset, usando algunas funciones del paquete sf. Parece que en las variables X e Y están las coordenadas:
NY <- sf::st_as_sf(NY, coords = c("X","Y"))
class(NY)[1] "sf" "data.frame"ggplot() +
geom_sf(data = NY, fill="transparent", color = "blue") +
theme_void()
Pero, para hacer nuestro análisis, ¿no necesitaríamos los límites de los condados de Nueva York? ¿Qué son estos puntos? Por ello trabajaremos con este shapefile (conjunto de datos inicial + límites de los condados de NY):
NY <- sf::st_read("data/NewYork/NY.shp", quiet=T)
sf::st_crs(NY) <- 32618 # WGS84(Zona 18) - https://epsg.io/32618
ggplot() +
geom_sf(data = NY, fill="transparent", color = "blue") +
theme_minimal()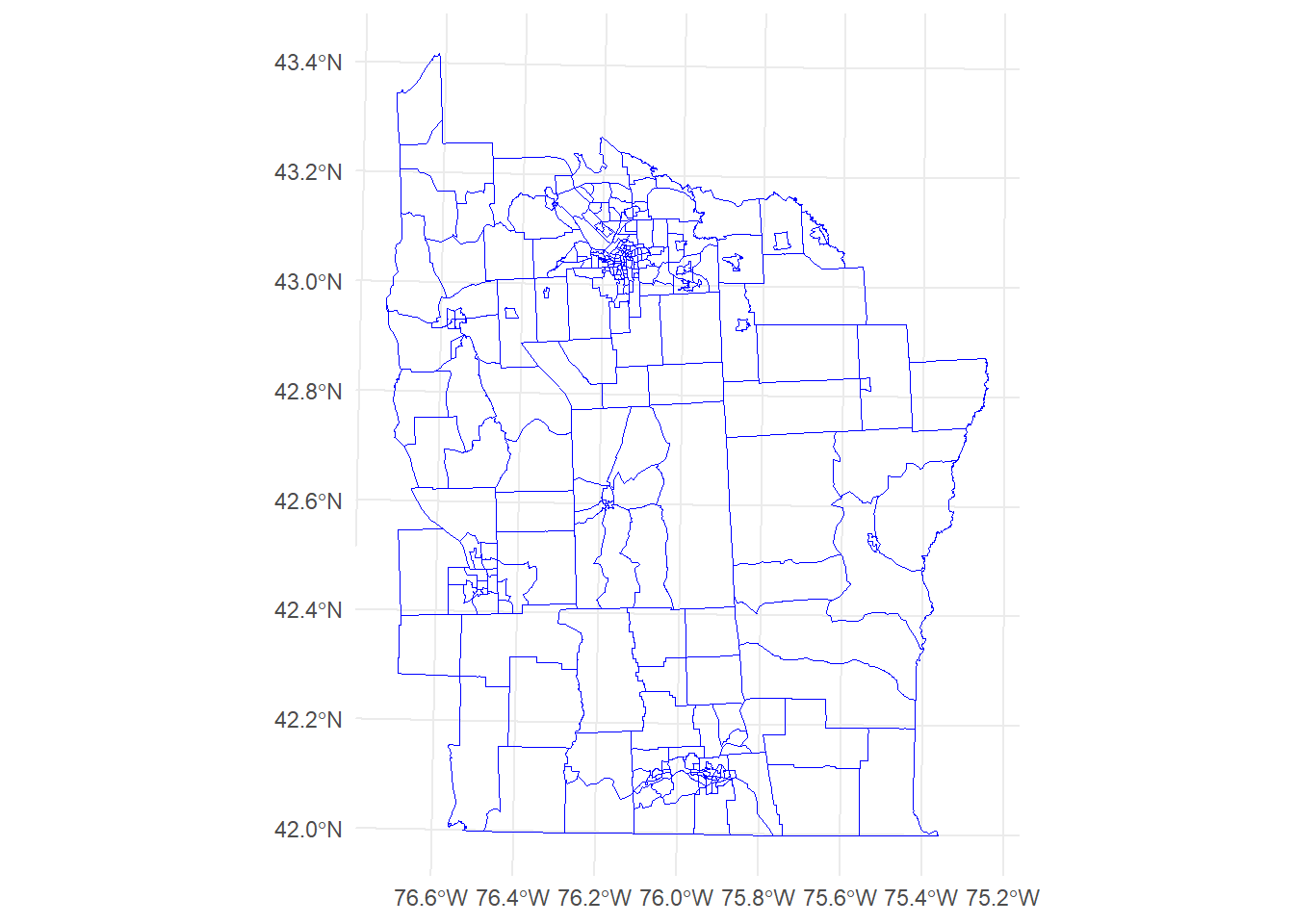
16.2.1 Contraste global de autocorrelación espacial
El estadístico (índice) I de Moran se define como el cociente entre la covarianza espacial de una variable y la varianza de la misma. En otras palabras, el índice I de Moran mide la autocorrelación espacial de una variable, es decir, hasta qué punto una variable es similar a sí misma en diferentes ubicaciones en el espacio. Matemáticamente, el índice I de Moran se puede expresar como:
\[ \begin{equation} I=\frac{n}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}} \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij} (y_i-\overline{y}) (y_j-\overline{y})}{\sum_{i=1}^n (y_i-\overline{y})^2} \end{equation} \]
Este índice \(I\) toma un valor comprendido entre \(−1\) y \(1\):
- Si \(I=0\) patrón espacial aleatorio, es decir, los datos están distribuidos al azar (algo similar al CSR en procesos puntuales).
- Si \(I>0\) autocorrelación espacial positiva, donde valores similares tienden a agruparse en el espacio.
- Si \(I<0\) valores similares tienden a estar dispersos en el espacio.
- Si \(I=1\) máxima concentración.
- Si \(I=-1\) máxima dispersión.
Veamos cómo sería el cálculo de \(I\), paso a paso, para la variable Casos (número de casos de leucemia observados para cada zona).
Con la función poly2nb() del paquete spdep obtenemos el número de vecinos (un objeto de clase list) que tiene cada zona. Por defecto el argumento queen toma valor TRUE:
wr <- spdep::poly2nb(NY, queen = FALSE) # queen = F equivale a rook = T
class(wr)[1] "nb"wr[1:6][[1]]
[1] 2 13 14 15 48 49 50
[[2]]
[1] 1 3 13 35 47
[[3]]
[1] 2 4 5 13 35
[[4]]
[1] 3 5 6 35
[[5]]
[1] 3 4 6 10 12
[[6]]
[1] 4 5 7 9 10 35summary(wr)Neighbour list object:
Number of regions: 281
Number of nonzero links: 1528
Percentage nonzero weights: 1.935133
Average number of links: 5.437722
Link number distribution:
1 2 3 4 5 6 7 8 9 10 11
6 8 18 53 67 48 49 20 8 2 2
6 least connected regions:
56 98 101 102 245 246 with 1 link
2 most connected regions:
35 83 with 11 linksDe este resumen obtenemos que:
- Estamos trabajando con 281 unidades geográficas (secciones censales).
- Se han identificado 1528 enlaces/conexiones entre polígonos adyacentes.
- El 1,93% de todos los posibles enlaces son no nulos (medida que ayuda a entender la densidad o la intensidad de la conectividad espacial).
- En promedio, cada unidad geográfica (polígono) tiene 5,44 vecinos.
- Existen 6 secciones censales con un único vecino; 8 con 2 vecinos, 18 con 3 vecinos…
- Las regiones menos conectadas son: 56, 98, 101, 102, 245 y 246.
- Las regiones más conectadas son: 35 y 83.
Representamos gráficamente la conectividad espacial de las regiones incluidas en el dataset:
xy <- sf::st_centroid(NY$geometry)
par(mar=rep(1,4))
plot(NY$geometry, border="blue")
plot(wr, xy, col="grey", add=TRUE)
Creamos una matriz con la lista de conexiones:
wm <- spdep::nb2mat(wr, style = "B") # ver apartado 2.4.2 de la teoría
dim(wm)[1] 281 281wm[1:6,1:11] [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
1 0 1 0 0 0 0 0 0 0 0 0
2 1 0 1 0 0 0 0 0 0 0 0
3 0 1 0 1 1 0 0 0 0 0 0
4 0 0 1 0 1 1 0 0 0 0 0
5 0 0 1 1 0 1 0 0 0 1 0
6 0 0 0 1 1 0 1 0 1 1 0A continuación, calculamos \(n\), \(y\) y \(\overline{y}\):
n <- nrow(NY)
y <- NY$Casos
ybar <- mean(y)Ahora necesitamos calcular \((y_i-\overline{y}) (y_j-\overline{y})\). Lo podemos hacer de dos formas:
# Método 1
dy <- y - ybar
g <- expand.grid(dy, dy)
yiyj <- g[,1] * g[,2]
# Método 2
yi <- rep(dy, each=n)
yj <- rep(dy, n)
yiyj <- yi * yjCreamos una matriz con los pares multiplicados:
pm <- matrix(yiyj, ncol=n)
round(pm[1:6, 1:9]) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 1 2 -1 -1 1 -1 0 -2 0
[2,] 2 4 -2 -2 2 -2 0 -4 0
[3,] -1 -2 1 1 -1 1 0 2 0
[4,] -1 -2 1 1 -1 1 0 2 0
[5,] 1 2 -1 -1 1 -1 0 -2 0
[6,] -1 -2 1 1 -1 1 0 2 0Y multiplicamos esa matriz por los pesos, imputando el ceros a los pares que no son adyacentes:
pmw <- pm * wm
wm[1:6, 1:9] [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
1 0 1 0 0 0 0 0 0 0
2 1 0 1 0 0 0 0 0 0
3 0 1 0 1 1 0 0 0 0
4 0 0 1 0 1 1 0 0 0
5 0 0 1 1 0 1 0 0 0
6 0 0 0 1 1 0 1 0 1round(pmw[1:6, 1:9]) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
1 0 2 0 0 0 0 0 0 0
2 2 0 -2 0 0 0 0 0 0
3 0 -2 0 1 -1 0 0 0 0
4 0 0 1 0 -1 1 0 0 0
5 0 0 -1 -1 0 -1 0 0 0
6 0 0 0 1 -1 0 0 0 0Ahora sumamos los valores: \[ \sum_{i=1}^{n} \sum_{j=1}^{n} w_{ij} (y_i-\overline{y}) (y_j-\overline{y}) \]
(spmw <- sum(pmw))[1] 707.5801El siguiente paso es dividir este valor por la suma de los pesos:
smw <- sum(wm)
(sw <- spmw / smw)[1] 0.463076Y obtenemos la inversa de la varianza de \(y\):
vr <- n / sum(dy^2)El último paso es calcular el índice \(I\) de Moran:
(MI <- vr * sw)[1] 0.1172854Ahora veremos cómo calcular este índice de una forma más sencilla. Solo necesitamos calcular previamente los pesos para cada zona con la función nb2listw():
ww <- spdep::nb2listw(wr, style = "B")
spdep::moran(x = NY$Casos,
listw = ww,
n = length(ww$neighbours), # n
S0=spdep::Szero(ww)) # smw$I
[1] 0.1172854
$K
[1] 3.630216Y así comprobamos que los cálculos realizados son correctos.
Ahora, si queremos contrastar si los casos de leucemia se producen al azar, o dicho de otra forma, que no dependen del lugar (ausencia de autocorrelación espacial) se puede ejecutar el test global de Moran, que nos proporciona el valor del índice \(I\), además de otra información de interés. Este test sobre la hipótesis nula de ausencia de autocorrelación espacial se calcula mediante la función moran.test().
spdep::moran.test(NY$Casos, listw=ww)
Moran I test under randomisation
data: NY$Casos
weights: ww
Moran I statistic standard deviate = 3.3848, p-value =
0.0003562
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.117285431 -0.003571429 0.001274927 Como podemos observar, el p-value obtenido en el test es suficientemente pequeño como para poder rechazar \(H_0\), es decir, rechazamos que no hay autocorrelación espacial, por lo que podemos concluir afirmando que hay una concentración espacial mayor de la que cabría esperar si los casos se repartieran aleatoriamente entre todo el territorio analizado.
16.2.2 Contraste local de autocorrelación espacial
El test de Moran comentado en el punto anterior es un test global de autocorrelación espacial. El valor obtenido con ese test global se puede dividir para conseguir test locales que permitan detectar clusters en donde las observaciones sean similares a las de su entorno, así como detectar outliers locales, también denominados puntos calientes o hotspots.
Como ya vimos en la teoría, en el gráfico de dispersión de Moran, de tipo scatterplot, aparecen en el eje de abscisas (eje X) los valores de la variable de interés y en el eje de ordenadas (eje Y) esos mismos valores retardados espacialmente (valores de variable multiplicados por los pesos correspondientes). A este gráfico, que está dividido en 4 cuadrantes (bajo-bajo, bajo-alto, alto-bajo y alto-alto), se suele añadir una recta con pendiente igual al índice de Moran \(I\), expresando la relación lineal existente entre los puntos del gráfico, permitiendo detectar qué puntos influyen en la recta de regresión construida y que, por tanto, son sospechosos de autocorrelación espacial (puntos calientes).
par(mar = c(2,2,1,2))
spdep::moran.plot(NY$Casos,listw=spdep::nb2listw(wr, style = "B"), col="blue")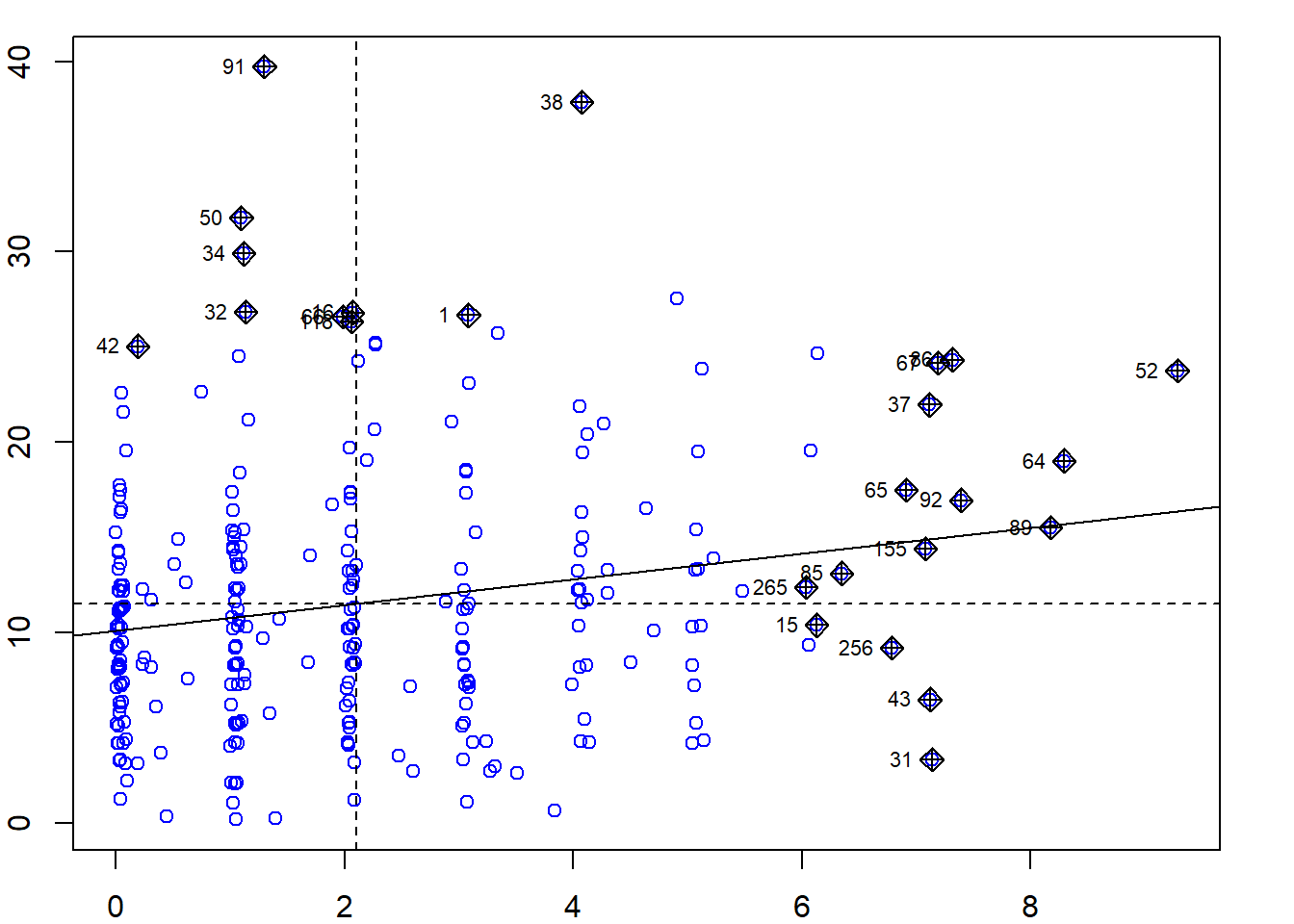
Para realizar los test locales usamos la función localmoran():
local.moran <- spdep::localmoran(NY$Casos, listw = ww)
head(round(local.moran,5)) Ii E.Ii Var.Ii Z.Ii Pr(z != E(Ii))
1 2.94571 -0.00603 1.65727 2.29289 0.02185
2 4.47163 -0.01767 4.87659 2.03292 0.04206
3 -2.03403 -0.00470 1.30017 -1.77973 0.07512
4 -0.50531 -0.00393 1.09016 -0.48020 0.63108
5 -1.03124 -0.00411 1.13773 -0.96296 0.33557
6 -0.20470 -0.00590 1.62741 -0.15584 0.87616tail(round(local.moran,5)) Ii E.Ii Var.Ii Z.Ii Pr(z != E(Ii))
276 1.84140 -0.02718 7.44552 0.68480 0.49347
277 0.06375 -0.00656 1.80286 0.05237 0.95824
278 -0.60535 -0.00821 2.23208 -0.39968 0.68939
279 0.31260 -0.00303 0.84375 0.34362 0.73114
280 0.18520 -0.01588 4.39756 0.09589 0.92361
281 0.05128 -0.00004 0.01043 0.50246 0.61535Los resultados del análisis de Moran local (LISA, por sus siglas en inglés Local Indicators of Spatial Association) proporcionan una medida de la autocorrelación espacial para cada ubicación individualmente. Para cada observación se ha obtenido:
- Ii: valor de Moran local para la ubicación \(i\).
- E.Ii: valor esperado de Ii bajo la hipótesis nula de aleatoriedad espacial.
- Var.Ii: varianza de Ii.
- Z.Ii: valor de \(Z\), calculado como \(\frac{(I_i-E(I_i))}{\sqrt{Var(I_i)}}\). Un valor \(Z\) alto en valor absoluto indica que la autocorrelación local es estadísticamente significativa.
- Pr(z != E(Ii)): p-value asociado con el valor \(Z\), indicando la probabilidad de observar tal valor \(Z\) bajo la hipótesis nula de aleatoriedad espacial.
Veamos gráficamente la presencia, en su caso, de autocorrelación espacial (local). Para ello, usaremos la librería tmap(Tennekes, 2018) y algunas funciones creadas ad-hoc:
match_palette <- function(patterns, classifications, colors){
classes_present <- base::unique(patterns)
mat <- matrix(c(classifications,colors), ncol = 2)
logi <- classifications %in% classes_present
pre_col <- matrix(mat[logi], ncol = 2)
pal <- pre_col[,2]
return(pal)
}Función para representar el LISA map:
lisa_map <- function(df, lisa, alpha = .05) {
clusters <- lisa_clusters(lisa,cutoff = alpha)
labels <- lisa_labels(lisa)
pvalue <- lisa_pvalues(lisa)
colors <- lisa_colors(lisa)
lisa_patterns <- labels[clusters+1]
pal <- match_palette(lisa_patterns,labels,colors)
labels <- labels[labels %in% lisa_patterns]
df["lisa_clusters"] <- clusters
tm_shape(df) +
tm_fill("lisa_clusters", labels = labels, palette = pal, style = "cat")
}Función para representar la significatividad:
significance_map <- function(df, lisa, permutations = 999, alpha = .05) {
pvalue <- lisa_pvalues(lisa)
target_p <- 1 / (1 + permutations)
potential_brks <- c(.00001, .0001, .001, .01)
brks <- potential_brks[which(potential_brks > target_p & potential_brks < alpha)]
brks2 <- c(target_p, brks, alpha)
labels <- c(as.character(brks2), "Not Significant")
brks3 <- c(0, brks2, 1)
cuts <- cut(pvalue, breaks = brks3, labels = labels)
df["sig"] <- cuts
pal <- rev(brewer.pal(length(labels), "Greens"))
pal[length(pal)] <- "#D3D3D3"
tm_shape(df) +
tm_fill("sig", palette = pal)
}w <- queen_weights(NY)
lisa <- local_moran(w, NY['Casos'])
lisa_map(NY, lisa)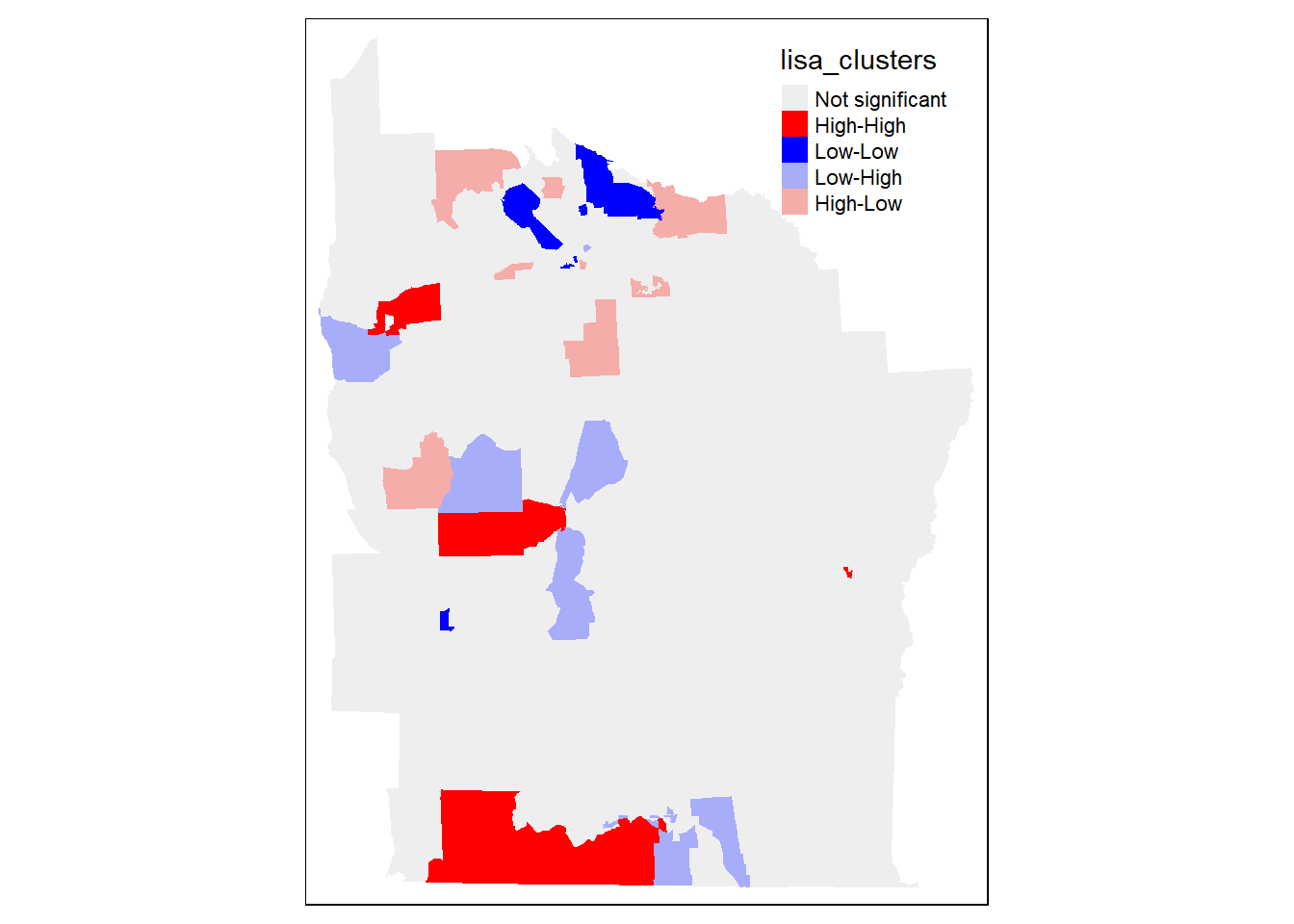
¿Cómo interpretamos este gráfico?
Los polígonos coloreados en rojo representan áreas con valores altos de la variable de interés (en este caso, “Casos”) que también están rodeadas por áreas con valores altos. Esto indica una autocorrelación espacial positiva significativa, donde áreas de alta incidencia están agrupadas juntas. Este tipo de clúster se conoce como un hotspot.
Los polígonos en azul muestran áreas con valores bajos de la variable que están rodeadas por áreas también con valores bajos. Igual que para el caso anterior, esto denota una autocorrelación espacial positiva significativa, pero en el extremo inferior de la escala de valores. Estas áreas pueden considerarse “coldspots”, donde la característica de interés es consistentemente baja y estas condiciones bajas están agrupadas.
El color lila indica áreas con valores bajos de la variable que están rodeadas por áreas con valores altos. Esto representa una discrepancia o contraste espacial significativo, donde áreas de baja incidencia están inmediatamente adyacentes a áreas de alta incidencia. Este patrón puede sugerir una forma de transición espacial o posiblemente áreas que están siendo impactadas por sus vecinos de alto valor de manera diferente.
Los polígonos pintados de rosa son áreas con valores altos de la variable que están rodeadas por áreas con valores bajos. Este es otro tipo de autocorrelación espacial negativa significativa, mostrando un contraste donde áreas de alta incidencia están cercanas a áreas de baja incidencia, sugiriendo posibles fronteras en la distribución espacial de la característica estudiada.
Finalmente, los polígonos en gris representan áreas donde la relación espacial local no es estadísticamente significativa según el nivel de significancia (alpha) especificado. Esto significa que no hay suficiente evidencia para afirmar que la distribución espacial de la variable de interés en estas áreas difiere de lo que se esperaría bajo un proceso espacial aleatorio.
16.3 Datos de España
Para afianzar lo aprendido en el bloque anterior, se propone analizar alguna variable de interés a nivel nacional (península). Los niveles de agregación de interés son Provincia e inferiores. Como ya hemos visto en sesiones anteriores, una forma sencilla de obtener la cartografía de las provincias españolas es usando el paquete mapSpain:
spain <- mapSpain::esp_get_prov() %>% filter(!codauto %in% c("04","05","18","19"))Ahora vamos a obtener, del INE, el número de habitantes y el número de personas jubiladas que había en cada provincia española en 2023, y así poder calcular (y proponer) un índice de dependencia (IDP), entendido como la proporción de personas jubiladas en relación con la población total.
jub23 <- readxl::read_xlsx("data/jub_esp_23.xlsx", range = "A10:B61", col_names = F)
colnames(jub23) <- c("PROV","jub")
jub23 <- jub23 %>%
tidyr::separate(PROV, into = c("cod_prov", "name_prov"), sep = " ", extra = "merge") %>%
dplyr::arrange(cod_prov)
head(jub23)# A tibble: 6 × 3
cod_prov name_prov jub
<chr> <chr> <dbl>
1 01 Araba/Álava 63
2 02 Albacete 63.2
3 03 Alicante/Alacant 369.
4 04 Almería 112.
5 05 Ávila 33.4
6 06 Badajoz 118. pob23 <- readxl::read_xlsx("data/pob_esp_23.xlsx", range = "A11:B114", col_names = F)
colnames(pob23) <- c("PROV","pob")
pob23 <- pob23 %>%
dplyr::mutate(PROV = if_else(PROV == "Total", lag(PROV), PROV)) %>%
dplyr::filter(!is.na(pob)) %>%
tidyr::separate(PROV, into = c("cod_prov", "name_prov"), sep = " ", extra = "merge") %>%
dplyr::arrange(cod_prov)
head(pob23)# A tibble: 6 × 3
cod_prov name_prov pob
<chr> <chr> <dbl>
1 01 Araba/Álava 336308
2 02 Albacete 387529
3 03 Alicante/Alacant 1955268
4 04 Almería 753364
5 05 Ávila 159764
6 06 Badajoz 666049dt <- full_join(pob23, jub23, by=c("cod_prov","name_prov"))
dt <- dt %>% mutate(IDP = jub/(pob/1000))
head(dt)# A tibble: 6 × 5
cod_prov name_prov pob jub IDP
<chr> <chr> <dbl> <dbl> <dbl>
1 01 Araba/Álava 336308 63 0.187
2 02 Albacete 387529 63.2 0.163
3 03 Alicante/Alacant 1955268 369. 0.189
4 04 Almería 753364 112. 0.148
5 05 Ávila 159764 33.4 0.209
6 06 Badajoz 666049 118. 0.177Con esto, solo nos falta añadir la variable que hemos creado a la cartografía…
spain <- left_join(spain, dt, by=c("cpro"="cod_prov"))…y representar gráficamente (esta vez con tmap), para comprobar que todo está correcto hasta el momento:
spain %>%
tmap::tm_shape() +
tmap::tm_polygons(col = "IDP", border.col = "grey50",
style = "jenks", n=6,
palette = "Blues") +
tmap::tm_layout(frame = F,
legend.position = c("right","bottom"),
inner.margins = rep(0,4))
A partir de aquí, el procedimiento de análisis sería el mismo al realizado anteriormente…
w <- queen_weights(spain)
lisa <- local_moran(w, spain['IDP'])
lisa_map(spain, lisa)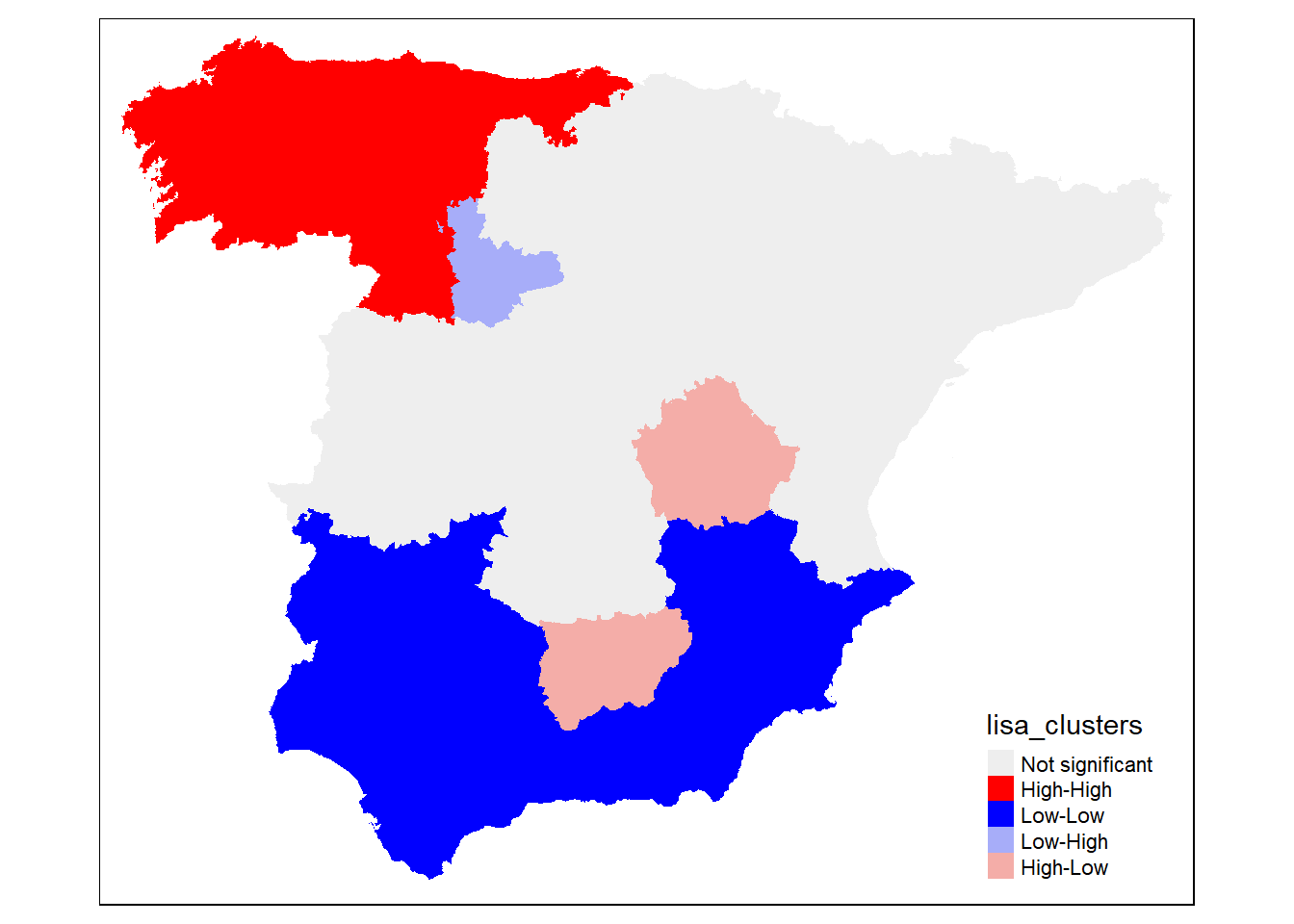
significance_map(spain, lisa)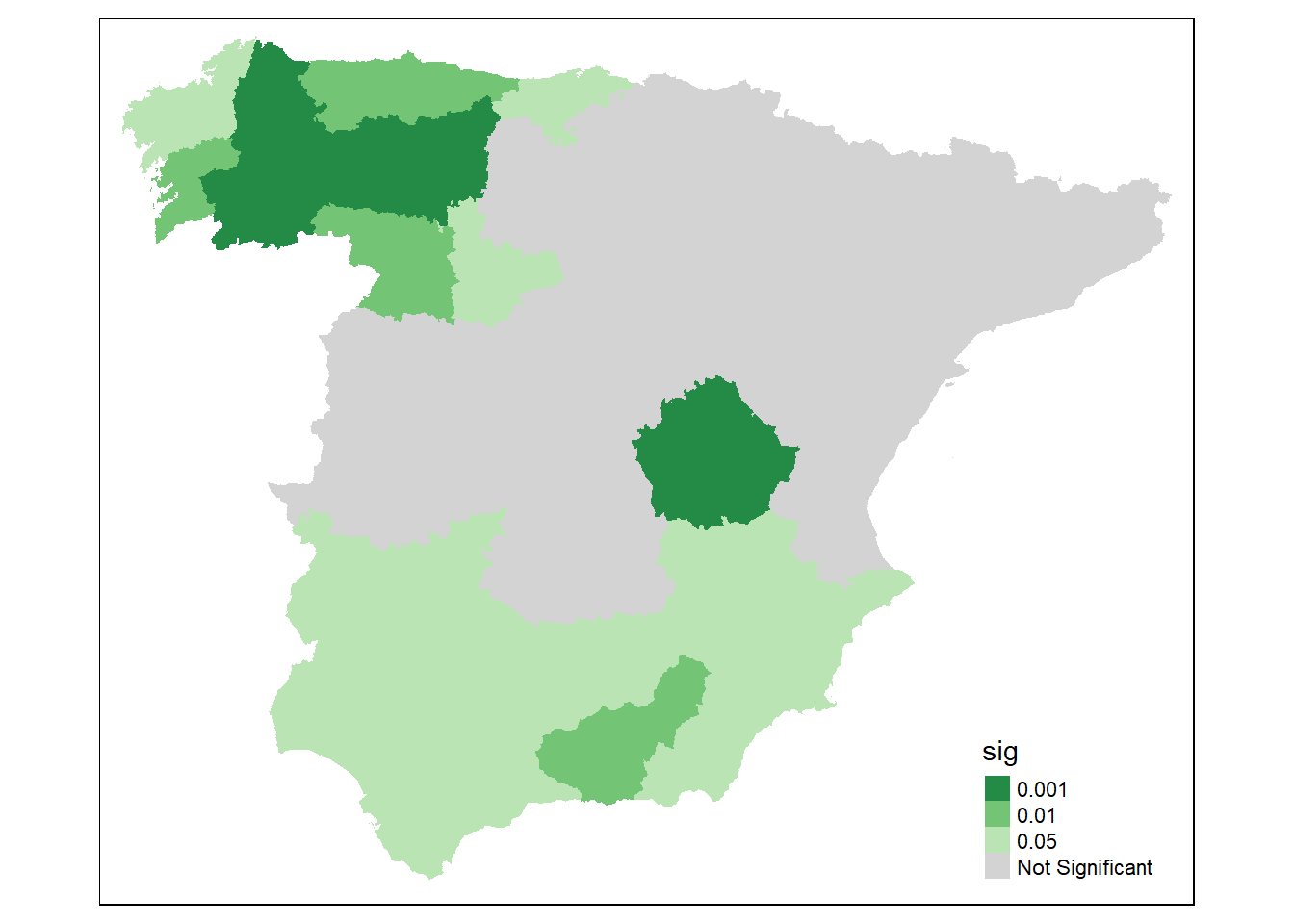
lisa_map(spain, lisa) +
tm_borders() +
tm_layout(title = "Local Moran Cluster Map of IDP", legend.outside = TRUE)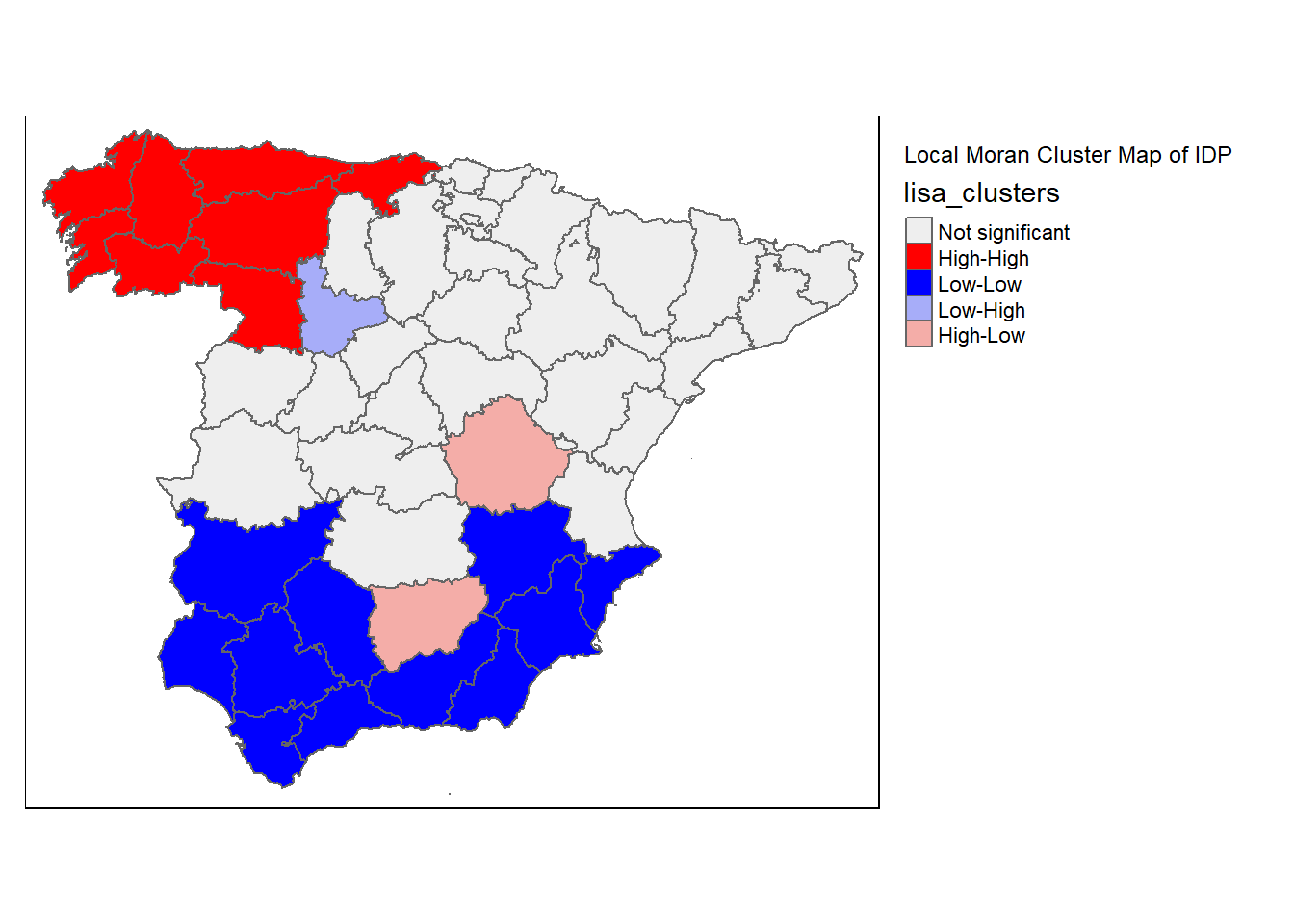
tmap_mode("view")tmap mode set to interactive viewinglisa_map(spain, lisa) +
tm_borders() +
tm_layout(title = "Local Moran Cluster Map of IDP",legend.outside = TRUE)tmap_mode("plot")tmap mode set to plotting