library(tidyverse)
library(sf)
library(mapSpain)
library(leaflet)
library(leaflet.extras)
library(spatstat)
library(sp)
library(splancs)13 Procesos puntuales
13.1 Introducción
En esta sesión llevaremos a la práctica aquellos aspectos relacionados con los Modelos Espaciales Puntuales (Spatial Point Patterns). Como vimos en la sesión de teoría, el análisis de procesos puntuales es una rama de la estadística espacial que se enfoca en el estudio de la distribución y estructura de puntos dentro de un espacio. Estos puntos pueden representar una amplia variedad de fenómenos en el mundo real, como la ubicación de árboles en un bosque, hogares en una ciudad, o incluso crímenes en un área urbana. El objetivo principal de este análisis es entender los patrones subyacentes que rigen la distribución de estos eventos, determinando si se distribuyen de manera aleatoria, uniforme o agrupada. Este tipo de análisis permite (puede permitir) conocer en profundidad los mecanismos que generan dichos patrones, facilitando la toma de decisiones en áreas como la ecología, epidemiología, criminología y planificación urbana, entre otras. Al aplicar métodos estadísticos y matemáticos para analizar los procesos puntuales, los investigadores pueden identificar correlaciones, tendencias y anomalías en los datos, proporcionando una comprensión más profunda de los procesos y fenómenos estudiados.
13.2 Librerías
En esta práctica utilizaremos algunos paquetes ya habituales (tidyverse, sf, mapSpain y leaflet) junto a las librerías spatstat (Baddeley et al., 2022) (permite realizar una amplia gama de análisis estadísticos espaciales, incluyendo la estimación de intensidad, análisis de marcas, simulaciones, así como manejar y analizar patrones de puntos), sp (Pebesma y Bivand, 2023) (precursor de sf, útil para manejar y analizar datos espaciales y geográficos) y splancs (Rowlingson y Diggle, 2023) (alternativa y/o complemento de spatstat).
Cargamos las librerías:
13.3 Trabajando con datos generados al azar
En primer lugar, vamos a trabajar con localizaciones generadas al azar. Creamos una ventana de observación de tamaño \([0,1] \times [0,1]\) con n ubicaciones:
n = 50
set.seed(123)
xy <- data.frame(x = runif(n), y = runif(n)) %>%
st_as_sf(coords = c("x", "y"))
w1 <- st_bbox(c(xmin = 0, ymin = 0, xmax = 1, ymax = 1)) %>%
st_as_sfc()
ggplot() +
geom_sf(data = w1) +
geom_sf(data = xy) +
theme_classic()
Estos puntos están distribuidos uniformemente, es decir, existe una Aleatoriedad Espacial Completa, o lo que es lo mismo, Complete Spatial Randomness (CSR).
No obstante, esta misma distribución de puntos, en una región más grande, como la que se muestra a continuación, no seguirá una distribución uniforme, por lo que no existirá CSR:
w2 = st_sfc(st_point(c(0.5, 0.5))) %>%
st_buffer(1)
ggplot() +
geom_sf(data = w2) +
geom_sf(data = xy) +
theme_classic()
Los patrones de puntos en spatstat son objetos de la clase ppp (2D point pattern o planar point pattern) que contienen puntos y una ventana de observación (un objeto de la clase owin). Podemos crear un ppp a partir de los puntos generados anteriormente:
as.ppp(xy)Planar point pattern: 50 points
window: rectangle = [0.0246137, 0.9942698] x [0.0006248, 0.984957]
unitsComo vemos a continuación, cuando no se especifica ninguna ventana, el cuadro delimitador de los puntos se utiliza como ventana de observación.
pp1 <- as.ppp(xy)
class(pp1)[1] "ppp"plot(pp1, axes = T)
En cambio, si indicamos ese argumento…
pp1 <- as.ppp(c(w1, st_geometry(xy)))
plot(pp1, axes = T)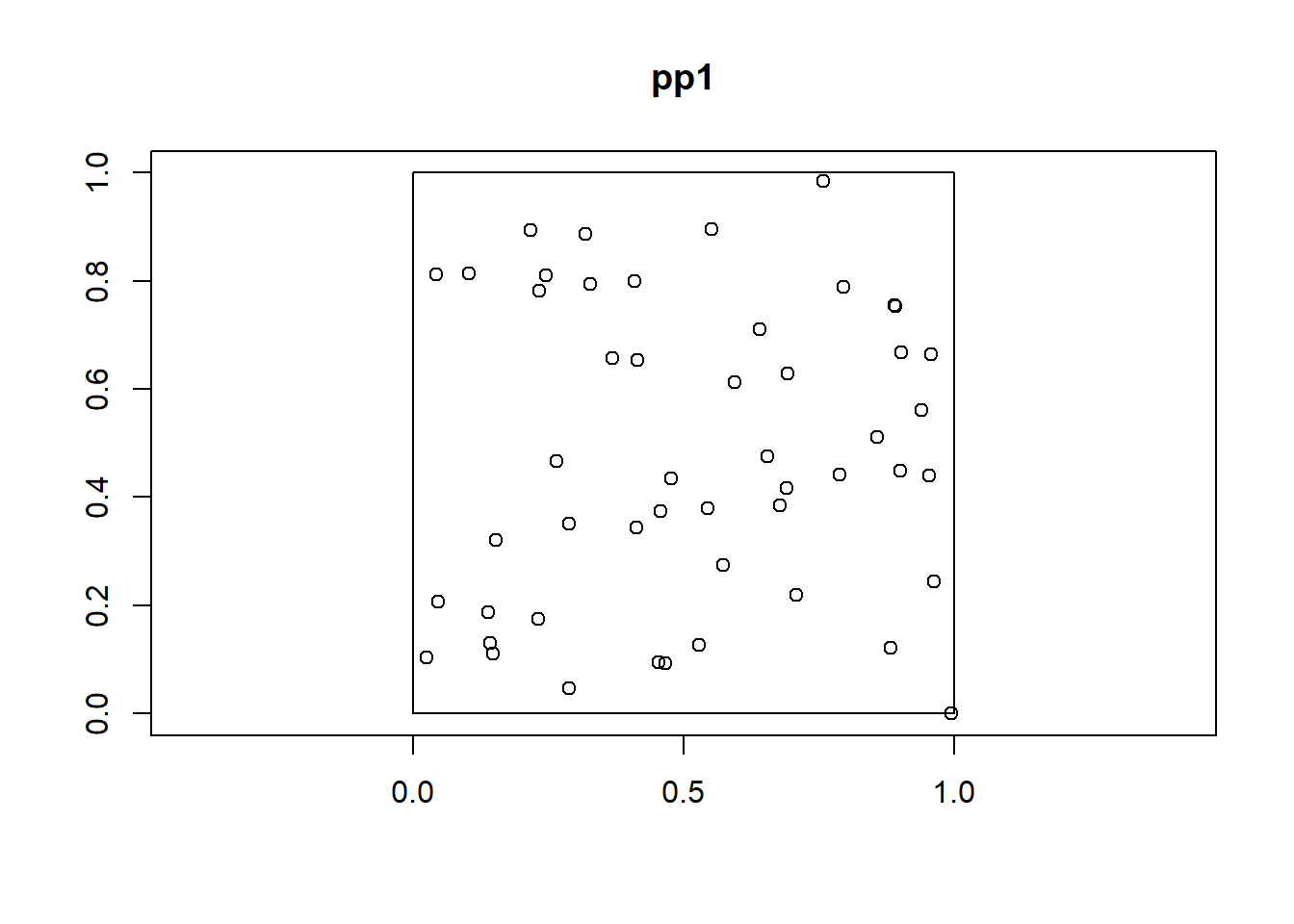
(pp1 = c(w1, st_geometry(xy)) %>% as.ppp())Planar point pattern: 50 points
window: polygonal boundary
enclosing rectangle: [0, 1] x [0, 1] unitsY de forma análoga para la segunda ventana:
pp2 <- as.ppp(c(w2, st_geometry(xy)))
plot(pp2, axes = T)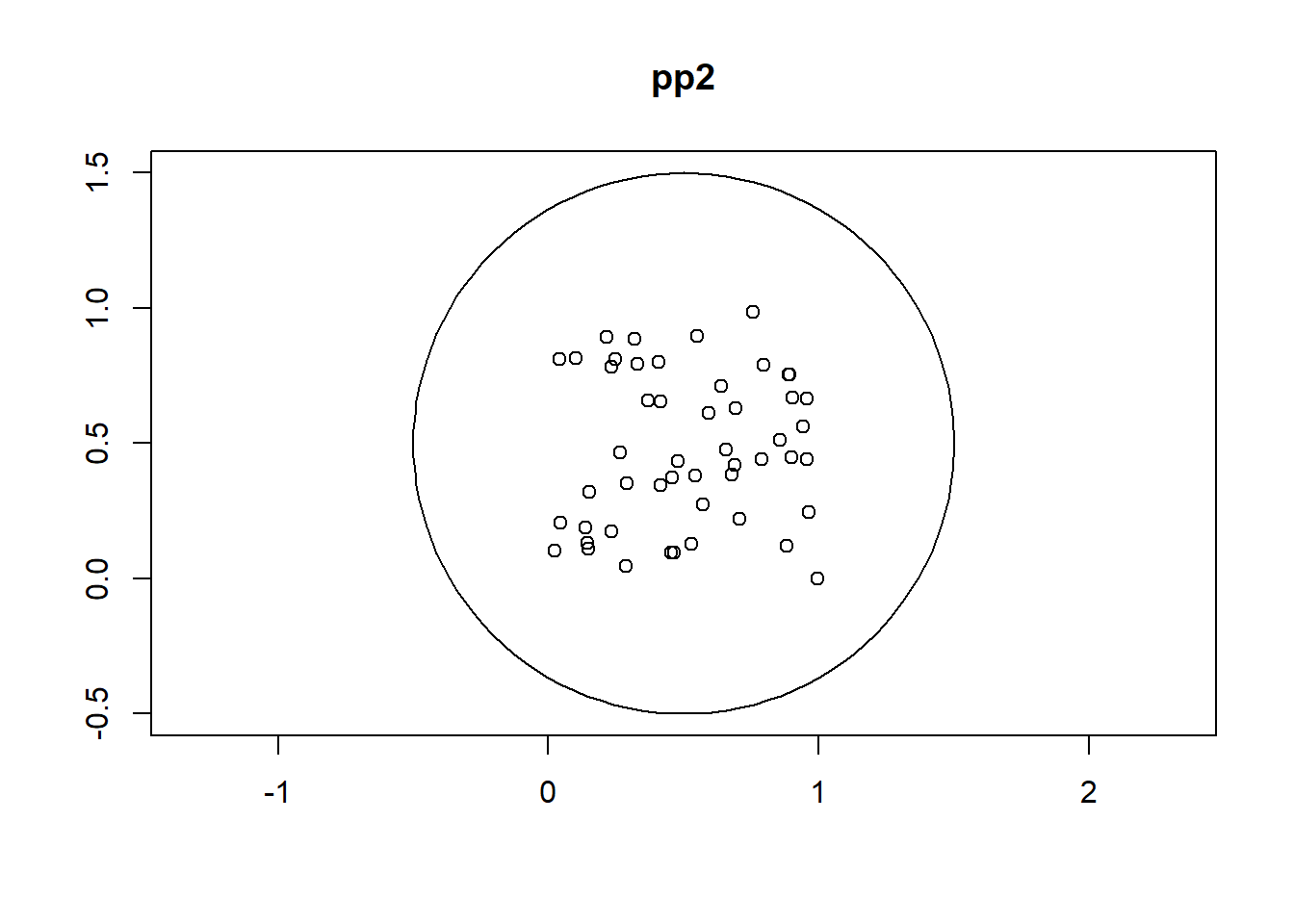
(pp2 = c(w2, st_geometry(xy)) %>% as.ppp())Planar point pattern: 50 points
window: polygonal boundary
enclosing rectangle: [-0.5, 1.5] x [-0.5, 1.5] units13.3.1 Quadrant test
Para comprobar la homogeneidad (recordemos que CSR se formaliza matemáticamente con un Proceso de Poisson homogéneo de parámetro \(\lambda\)) podemos realizar un conteo de cuadrantes (Quadrant test)…
par(mfrow = c(1, 2), mar = rep(0, 4))
q1 = quadratcount(pp1, nx=3, ny=3)
q2 = quadratcount(pp2, nx=3, ny=3)
plot(q1, main = "")
plot(xy, add = TRUE)
plot(q2, main = "")
plot(xy, add = TRUE)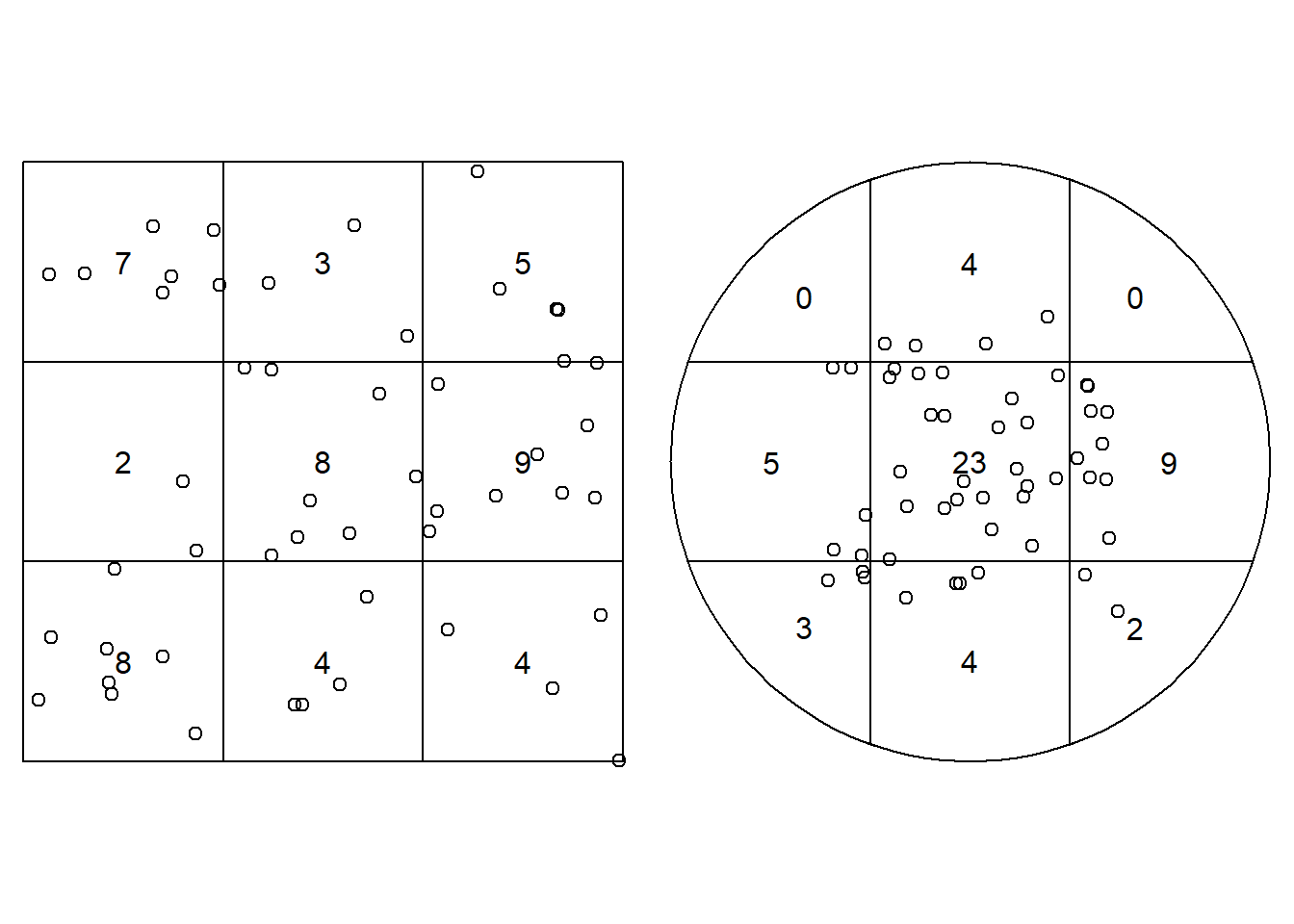
…y comparar mediante un test \(\chi^2\) de bondad de ajuste:
quadrat.test.ppp(pp1, nx=3, ny=3)
Chi-squared test of CSR using quadrat counts
data: pp1
X2 = 9.04, df = 8, p-value = 0.6779
alternative hypothesis: two.sided
Quadrats: 9 tiles (irregular windows)quadrat.test.ppp(pp2, nx=3, ny=3)
Chi-squared test of CSR using quadrat counts
data: pp2
X2 = 48.197, df = 8, p-value = 1.812e-07
alternative hypothesis: two.sided
Quadrats: 9 tiles (irregular windows)La hipótesis nula (\(H_0\)) para este test es que el patrón de puntos es completamente aleatorio. Por ello, realizado el test, un p-value elevado (típicamente mayor que 0.05), sugiere que no hay suficiente evidencia para rechazar la hipótesis nula de CSR, es decir, que la distribución de puntos dentro del área de estudio podría ser el resultado de un proceso aleatorio.
No obstante, lo anterior, y como vimos en la teoría, este método es poco fiable. Por ello, es más frecuente utilizar métodos basados en distancias.
13.4 Trabajando con datos usados en los manuales
El paquete spatstat contiene varios conjuntos de datos que nos van a permitir realizar análisis de tipo discreto (procesos puntuales):
cellscontiene la localización de 42 células observadas bajo microscopio;
japanesepinescontiene la localización de 65 pinos negros japoneses;
redwoodscontiene la localización de 62 secuoyas de California.
par(mfrow = c(1,3))
plot(cells)
plot(japanesepines)
plot(redwood)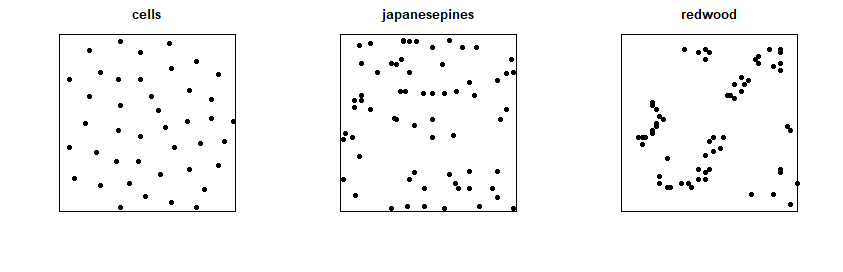
La aleatoriedad CSR se verifica si las diferencias (gráficas) entre el modelo teórico \(G(w)\) y la distribución empírica \(\hat{G}(w)\) no son grandes, para un conjunto de distancias \(r\) razonable.
Como el modelo teórico no es sencillo de manejar (fórmula vista en la teoría), lo que hacemos es, utilizando la función envelope(), generar muchas simulaciones del proceso puntual (las que consideremos mediante el parámetro nsim), en este caso G, para lo que utilizamos el argumento fun=Gest. La función envelope() solo admite datos del tipo ppp.
De esta forma, obtendremos unos “entornos de confianza” entre los que debería de estar la distribución empírica \(\hat{G}(w)\). En estos entornos se puede fijar el coeficiente de confianza mediante el argumento nrank, indicando cuántos de los valores simulados se deben eliminar a cada lado del entorno. Por ejemplo, si fijamos nrank=2 tendremos entornos de confianza del 96%.
A continuación se muestran los gráficos de los pares \((G(w), \hat{G}(w))\) para los tres ejemplos anteriores:
data(cells)
env_cells <- envelope(cells, fun=Gest, nsim=100, nrank=2, verbose = F)
plot(env_cells, main="Entorno de Confianza para 'cells'")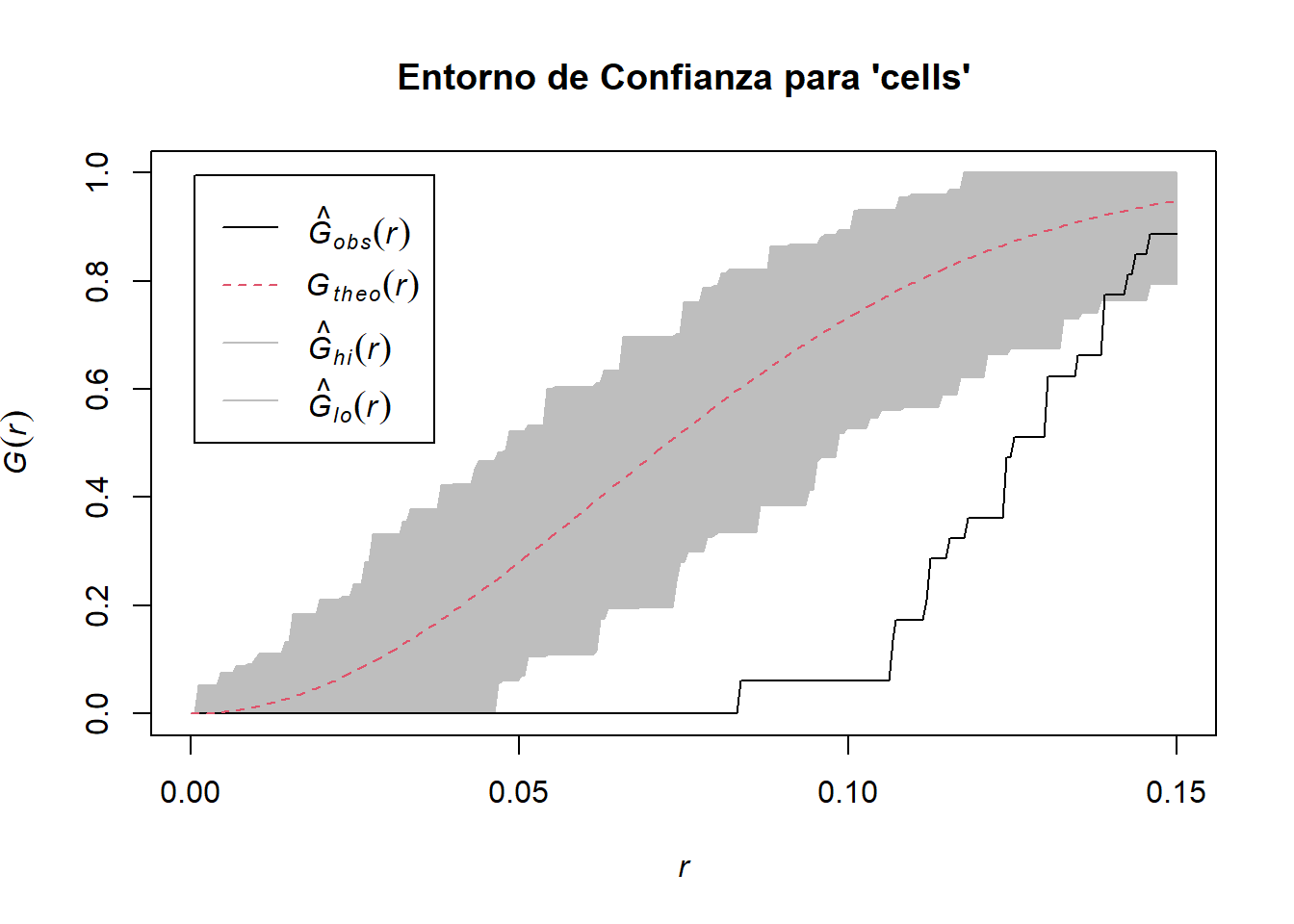
data(japanesepines)
env_japanesepines <- envelope(japanesepines, fun=Gest, nsim=100, nrank=2, verbose = F)
plot(env_japanesepines, main="Entorno de Confianza para 'japanesepines'")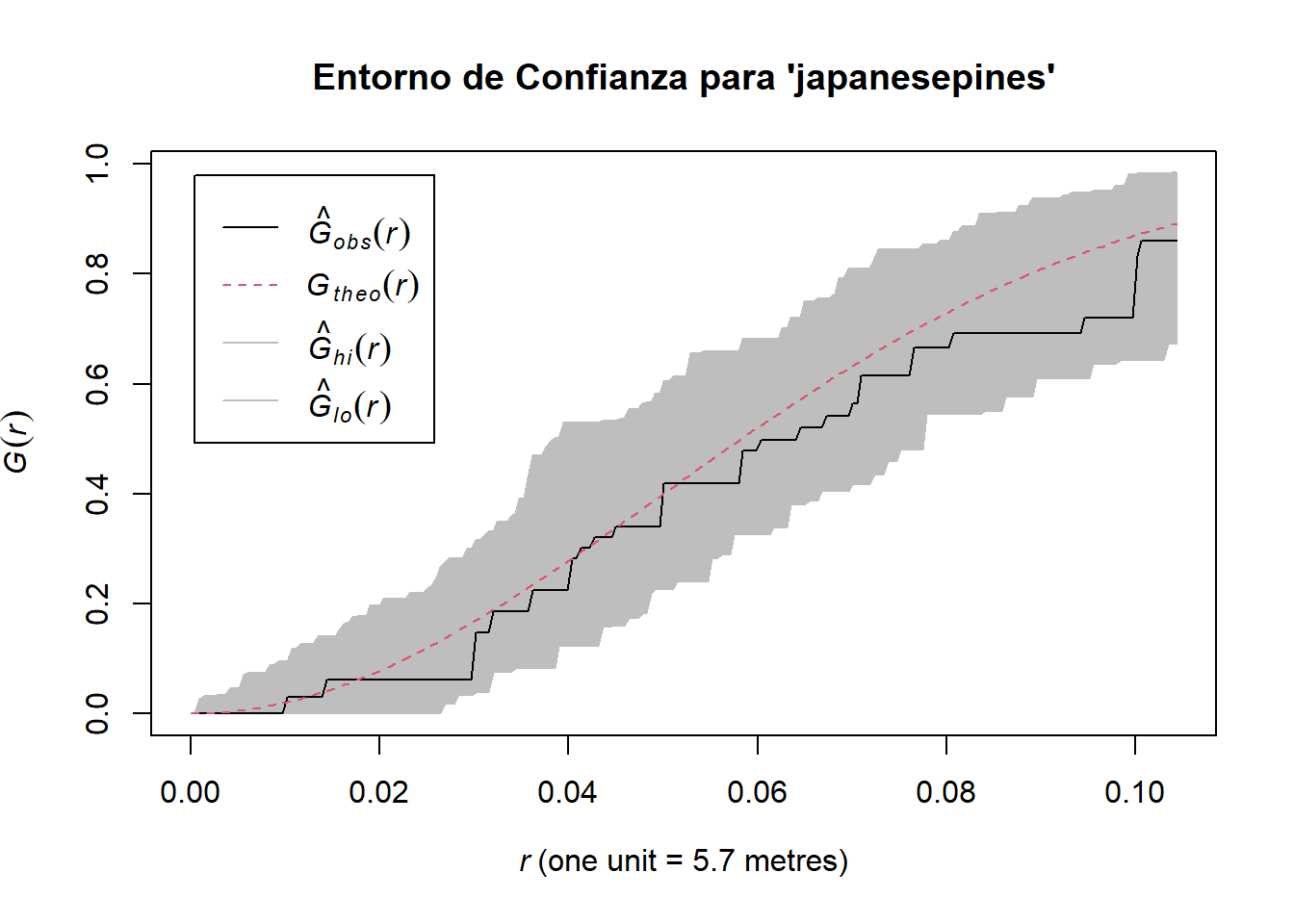
data(redwood)
env_redwood <- envelope(redwood, fun=Gest, nsim=100, nrank=2, verbose = F)
plot(env_redwood, main="Entorno de Confianza para 'redwood'")
Como se puede observar, solamente en el caso de los pinos negros japoneses (japanesepines) se tiene la Aleatoriedad Espacial Completa (CSR).
13.4.1 Ajuste de Modelos Espaciales Puntuales
Rechazar la Aleatoriedad Espacial Completa (CSR) implica que existe algún tipo de relación entre las localizaciones. Para estimar la intensidad del Proceso de Poisson no homogégeno mediante técnicas no paramétricas utilizaremos el estimador núcleo suavizado, ejecutando la función kernel2d de la librería splancs. Los argumentos de esta función son básicamente tres:
- los datos en formato
ppp;
- un polígono en el que queramos obtener las estimaciones (en nuestro caso un cuadrado de lado 1);
- el nivel de suavizado h.
En primer lugar debemos determinar el nivel de suavizado h, para lo que se suele utilizar el criterio propuesto por Diggle (1985) y Berman y Diggle (1989) consistente en elegir el primer valor en el que se consigue minimizar el error cuadrático medio del estimador kernel que tratamos de construir. Para ello utilizaremos la función mse2d de la librería splancs. Los argumentos de esta función son básicamente cuatro:
- los datos en formato
ppp;
- un polígono (en el que queramos obtener las estimaciones);
- el número de iteraciones que queremos considerar;
- el valor máximo admitido para h.
En este caso utilizaremos un conjunto de datos llamado redwoodfull, el cual contiene 195 localizaciones.
data(redwoodfull)
summary(redwoodfull)Planar point pattern: 195 points
Average intensity 195 points per square unit
Coordinates are given to 16 decimal places
Window: rectangle = [0, 1] x [0, 1] units
Window area = 1 square unitclass(redwoodfull)[1] "ppp"par(mar = c(2,2,1,2))
plot(redwoodfull, pch=16)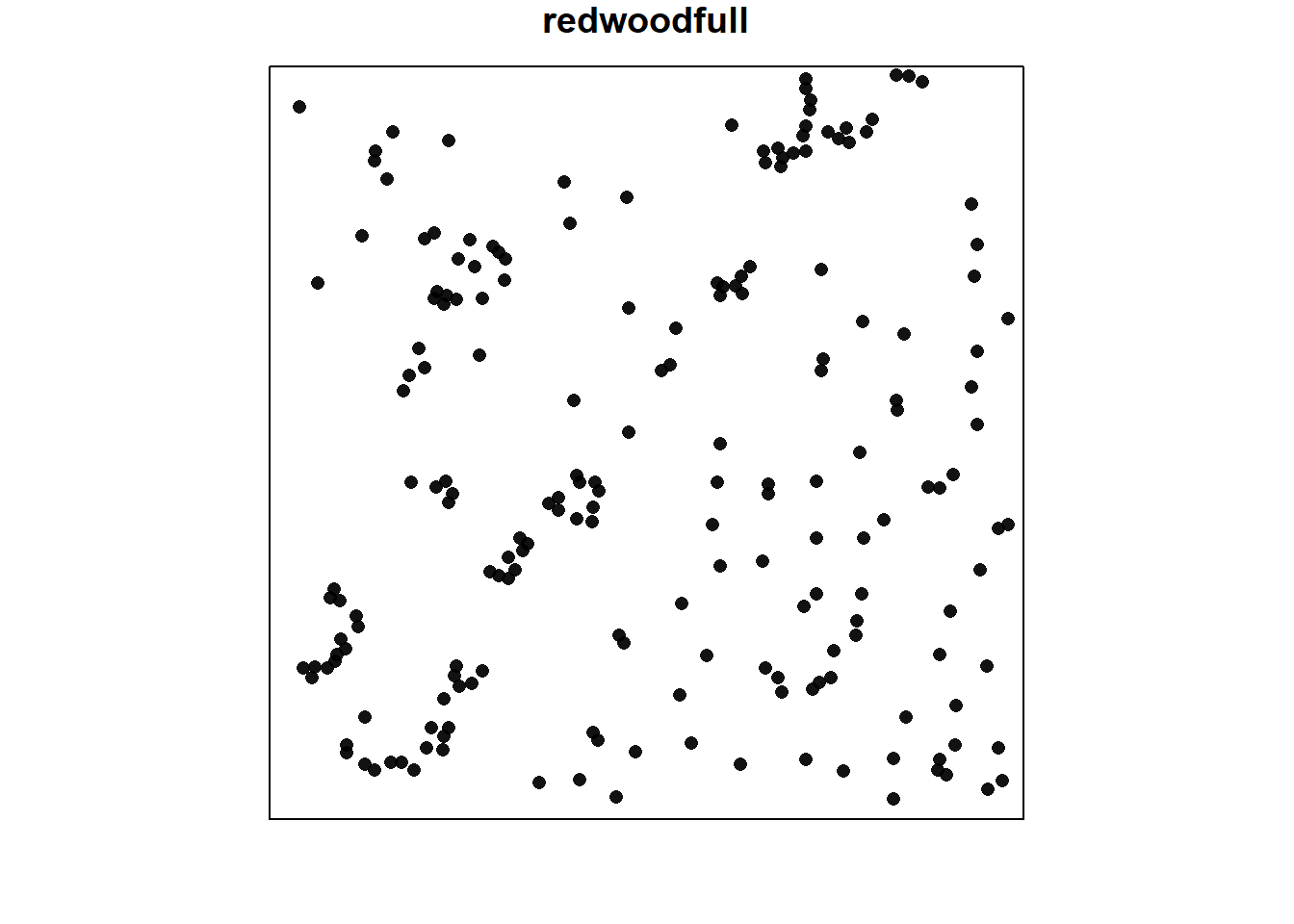
En primer lugar, creamos el polígono en el que vamos a estimar la intensidad (un cuadrado, de lado 1), definido mediante los dos vértices extremos.
poli <- as.points(list(x=c(0,0,1,1), y=c(0,1,1,0)))
class(poli)[1] "matrix" "array" A continuación, obtenemos 100 valores del error cuadrático medio (MSE) para 100 valores de h, utilizando la función mse2d, considerando que el valor 0.15 es el máximo admisible. Es decir, obtenemos 100 pares de valores \((h,MSE)\). Podríamos representarlos para ver en qué \(h\) se alcanza el menor MSE, pero es más sencillo ejecutar el código que se muestra a continuación:
G <- Gest(as(redwoodfull, "ppp"))
#summary(G)
max(G$r)[1] 0.1370884suavizados <- mse2d(pts = as.points(as(redwoodfull,"ppp")),
poly = poli,
nsmse = 100,
range = 0.15)
suavizados$h[which.min(suavizados$mse)][1] 0.039Ahora que ya sabemos que el suavizado a utilizar será \(h=0.039\) (poco suave), podemos obtener las estimaciones de la intensidad utilizando la función kernel2d.
a <- kernel2d(pts = as.points(as(redwoodfull,"ppp")),
poly = poli,
h0 = 0.039)Xrange is 0 1
Yrange is 0 1
Doing quartic kernela$x
[1] 0.025 0.075 0.125 0.175 0.225 0.275 0.325 0.375 0.425 0.475
[11] 0.525 0.575 0.625 0.675 0.725 0.775 0.825 0.875 0.925 0.975
$y
[1] 0.025 0.075 0.125 0.175 0.225 0.275 0.325 0.375 0.425 0.475
[11] 0.525 0.575 0.625 0.675 0.725 0.775 0.825 0.875 0.925 0.975
$z
[,1] [,2] [,3] [,4] [,5]
[1,] 0.000000 0.00000 0.000000 346.22702 257.505065
[2,] 0.000000 263.08203 130.552242 737.75591 1433.597943
[3,] 67.650059 997.53903 456.284743 85.54036 644.737262
[4,] 58.237839 1029.60184 140.661326 0.00000 0.000000
[5,] 1.017851 689.08798 1188.774087 772.58520 227.960271
[6,] 0.000000 16.23359 115.475658 941.50996 358.553808
[7,] 73.233872 62.08788 0.000000 14.85691 4.572200
[8,] 206.219554 203.55504 0.000000 0.00000 0.000000
[9,] 291.540413 394.48283 511.576884 0.00000 76.882713
[10,] 295.762993 276.61032 166.985759 0.00000 505.502370
[11,] 0.000000 97.87669 94.137114 225.50285 0.000000
[12,] 0.000000 163.59137 175.814369 190.14137 297.510561
[13,] 17.398580 313.37044 5.587387 67.42803 95.767460
[14,] 0.000000 107.17942 37.159796 761.74874 249.458137
[15,] 1.261076 361.76174 36.005208 852.78716 321.350524
[16,] 66.566405 255.94066 0.000000 157.54987 518.034039
[17,] 352.192874 326.04295 259.409363 46.01497 5.832133
[18,] 150.004532 788.62299 240.569422 85.89283 268.795921
[19,] 203.252476 551.54333 322.544755 247.23461 220.607699
[20,] 484.503887 560.75231 172.354693 103.43437 166.672078
[,6] [,7] [,8] [,9] [,10]
[1,] 0.00000 0.00000 0.000000 0.00000 0.00000
[2,] 745.42055 457.11973 0.000000 0.00000 0.00000
[3,] 668.01706 63.64564 0.000000 0.00000 0.00000
[4,] 0.00000 0.00000 0.000000 210.19110 155.58878
[5,] 0.00000 0.00000 17.260470 1010.64711 363.23509
[6,] 0.00000 498.02034 26.926749 229.52462 15.74125
[7,] 28.98349 1331.07378 994.653778 36.08589 0.00000
[8,] 0.00000 20.20949 413.176836 1008.74349 142.25642
[9,] 16.47733 0.00000 455.252188 1453.59455 582.36782
[10,] 194.79941 0.00000 4.725359 112.89403 85.58992
[11,] 201.52601 46.17050 0.000000 0.00000 0.00000
[12,] 144.93324 210.72855 267.509258 270.88956 249.43300
[13,] 0.00000 284.51564 129.740014 250.23216 191.07368
[14,] 109.20059 177.28003 86.705641 462.74206 172.79542
[15,] 447.51638 253.73614 313.464864 209.40205 192.71860
[16,] 616.37088 190.24960 318.484588 19.30247 266.48602
[17,] 47.33662 23.99048 300.793398 167.91126 43.78684
[18,] 166.66701 0.00000 0.000000 515.20891 320.33996
[19,] 227.01815 247.04895 70.191999 165.56069 219.43563
[20,] 0.00000 146.06316 593.984710 233.44434 0.00000
[,11] [,12] [,13] [,14] [,15]
[1,] 0.000000 0.000000 0.000000 1.231005 80.760342
[2,] 0.000000 0.000000 0.000000 73.831479 255.795954
[3,] 0.000000 1.660308 0.000000 0.000000 8.547078
[4,] 40.521003 631.316971 383.386820 24.982078 2.687990
[5,] 0.000000 212.091732 328.484882 1098.870417 783.829013
[6,] 0.000000 55.152611 299.103559 464.659287 924.290244
[7,] 0.000000 0.000000 18.936668 67.917172 620.092854
[8,] 52.713636 117.802852 0.000000 0.000000 0.000000
[9,] 92.238331 169.282634 0.000000 6.207600 0.000000
[10,] 288.443847 8.937452 1.262551 309.466214 32.325344
[11,] 8.773861 378.324935 542.520277 194.867586 0.000000
[12,] 114.135978 3.138018 51.847629 301.603424 478.877579
[13,] 92.253379 0.000000 0.000000 560.725168 1381.068795
[14,] 0.000000 0.000000 0.000000 2.740853 90.244305
[15,] 0.000000 305.243126 421.177389 0.000000 297.720583
[16,] 87.466468 16.166819 144.839830 248.226195 41.844892
[17,] 375.735709 368.551975 190.223520 178.010855 0.000000
[18,] 33.094753 24.407034 87.809833 38.520055 0.000000
[19,] 285.299301 321.129152 281.254635 18.708314 348.904118
[20,] 116.071518 50.640795 194.298386 326.983362 81.960286
[,16] [,17] [,18] [,19] [,20]
[1,] 0.000000 0.000000 0.000000 218.18856 184.7937807
[2,] 22.364579 0.000000 0.000000 54.86350 33.3095894
[3,] 312.303218 86.042514 590.009357 143.13039 0.0000000
[4,] 194.889062 135.256666 416.463779 266.70479 0.0000000
[5,] 682.088704 26.539217 156.323906 193.13677 0.0000000
[6,] 737.157564 0.000000 24.531048 40.28812 0.0000000
[7,] 416.025217 0.000000 0.000000 0.00000 0.0000000
[8,] 167.285200 247.522273 138.193930 0.00000 0.0000000
[9,] 140.548046 128.794980 40.483723 0.00000 0.0000000
[10,] 4.127431 313.003381 17.897001 0.00000 0.0000000
[11,] 0.000000 6.717196 0.000000 0.00000 0.0000000
[12,] 0.000000 0.000000 0.000000 86.33333 0.0000000
[13,] 57.407964 0.000000 281.941639 300.94296 0.9446629
[14,] 0.000000 58.966335 1662.055452 481.76820 246.4922442
[15,] 39.190070 0.000000 679.046863 1369.82466 1015.2771578
[16,] 0.000000 0.000000 405.459192 1160.90396 5.9549490
[17,] 0.000000 0.000000 8.956447 311.20056 585.6226878
[18,] 0.000000 0.000000 0.000000 0.00000 551.0479873
[19,] 301.170426 294.494789 0.000000 0.00000 0.0000000
[20,] 101.211655 46.037611 0.000000 0.00000 0.0000000
$h0
[1] 0.039
$kernel
[1] "quartic"a1 <- a$x
a2 <- a$y
a3 <- a$z #valores estimados para las localizaciones dadasLa representación en tres dimensiones de valores \(z\) para los pares de datos \((x,y)\) la podemos hacer con la función persp:
par(mar=c(2,2,1,2))
persp(a1, a2, a3,
theta = 30, phi = 30, ltheta = 120, shade = 0.75,
expand = 0.5, col = "lightblue", ticktype="detailed",
xlab = "", ylab = "", zlab = "", main = "Intensidad")
No obstante, lo habitual es representar la densidad en un gráfico 2D:
den1 <- density(as(redwoodfull,"ppp"), sigma = bw.diggle)
par(mfrow = c(1,1), mar=c(2,2,1,2))
plot(den1, main = "Densidad")
plot(as(redwoodfull, "ppp"), add = TRUE)
13.5 Trabajando con datos reales
Probemos ahora a usar esta metodología con datos reales. En este caso, usaremos un dataset sobre los accidentes de tráfico con implicación de bicicletas acaecidos en Madrid durante todo 2023. Este dataset, accesible desde el Portal de datos abiertos de Madrid, está disponible aquí.
Cargamos el dataset y lo exploramos:
bici_23 <- readxl::read_xlsx("data/AccidentesBicicletas_2023.xlsx")
dim(bici_23)[1] 905 19glimpse(bici_23)Rows: 905
Columns: 19
$ num_expediente <chr> "2023S000057", "2023S000123", "2023S0…
$ fecha <dttm> 2023-01-02, 2023-01-03, 2023-01-03, …
$ hora <dttm> 1899-12-31 07:50:00, 1899-12-31 13:2…
$ localizacion <chr> "CALL. GOYA / CALL. LOMBIA", "AVDA. E…
$ numero <chr> "86", "100", "51", "39", "39", "27", …
$ cod_distrito <dbl> 4, 13, 7, 2, 3, 7, 11, 1, 1, 15, 12, …
$ distrito <chr> "SALAMANCA", "PUENTE DE VALLECAS", "C…
$ tipo_accidente <chr> "Colisión fronto-lateral", "Colisión …
$ estado_meteorológico <chr> "Nublado", "Despejado", "Despejado", …
$ tipo_vehiculo <chr> "Bicicleta", "Bicicleta EPAC (pedaleo…
$ tipo_persona <chr> "Conductor", "Conductor", "Conductor"…
$ rango_edad <chr> "De 55 a 59 años", "De 55 a 59 años",…
$ sexo <chr> "Hombre", "Hombre", "Hombre", "Mujer"…
$ cod_lesividad <chr> "NULL", "1", "3", "NULL", "2", "NULL"…
$ lesividad <chr> "NULL", "Atención en urgencias sin po…
$ coordenada_x_utm <chr> "442943.680", "443717.786", "441406.0…
$ coordenada_y_utm <chr> "4475109.106", "4469886.737", "447655…
$ positiva_alcohol <chr> "N", "N", "N", "N", "N", "N", "N", "N…
$ positiva_droga <chr> "NULL", "NULL", "NULL", "NULL", "NULL…Convertimos las coordenadas a valores numéricos:
bici_23$coordenada_x_utm <- as.numeric(bici_23$coordenada_x_utm)
bici_23$coordenada_y_utm <- as.numeric(bici_23$coordenada_y_utm)A partir del data.frame, creamos un objeto sf:
bici_23_sf <- sf::st_as_sf(bici_23,
coords = c("coordenada_x_utm",
"coordenada_y_utm"), crs = 25830)Comprobamos, con una muestra de 5 observaciones, que las coordenadas son coherentes con la info del dataset:
sf1 <- sf::st_transform(bici_23_sf, crs = 4326)
sf2 <- sf1[1:5,]
sf2 %>%
leaflet::leaflet() %>%
leaflet::addTiles() %>%
leaflet::addMarkers(popup = ~localizacion)
Convertimos el objeto sf en ppp. Para ello, primero debemos hacer la conversión a sp, tal y como se muestra a continuación:
bici_sp <- as(bici_23_sf, "Spatial")
xrange=range(bici_sp@coords[,1])
yrange=range(bici_sp@coords[,2])
W = owin(xrange=xrange, yrange=yrange)
#W2 = owin(xrange=c(437000, 447000), yrange=c(4470000,4480000))
bici_ppp <- as.ppp(X = coordinates(bici_sp), W = W)Warning: data contain duplicated pointsVeamos cómo se distribuyen los puntos (análisis exploratorio):
plot(bici_ppp, main="Accidentes de tráfico con implicación de bicicletas", axes = T)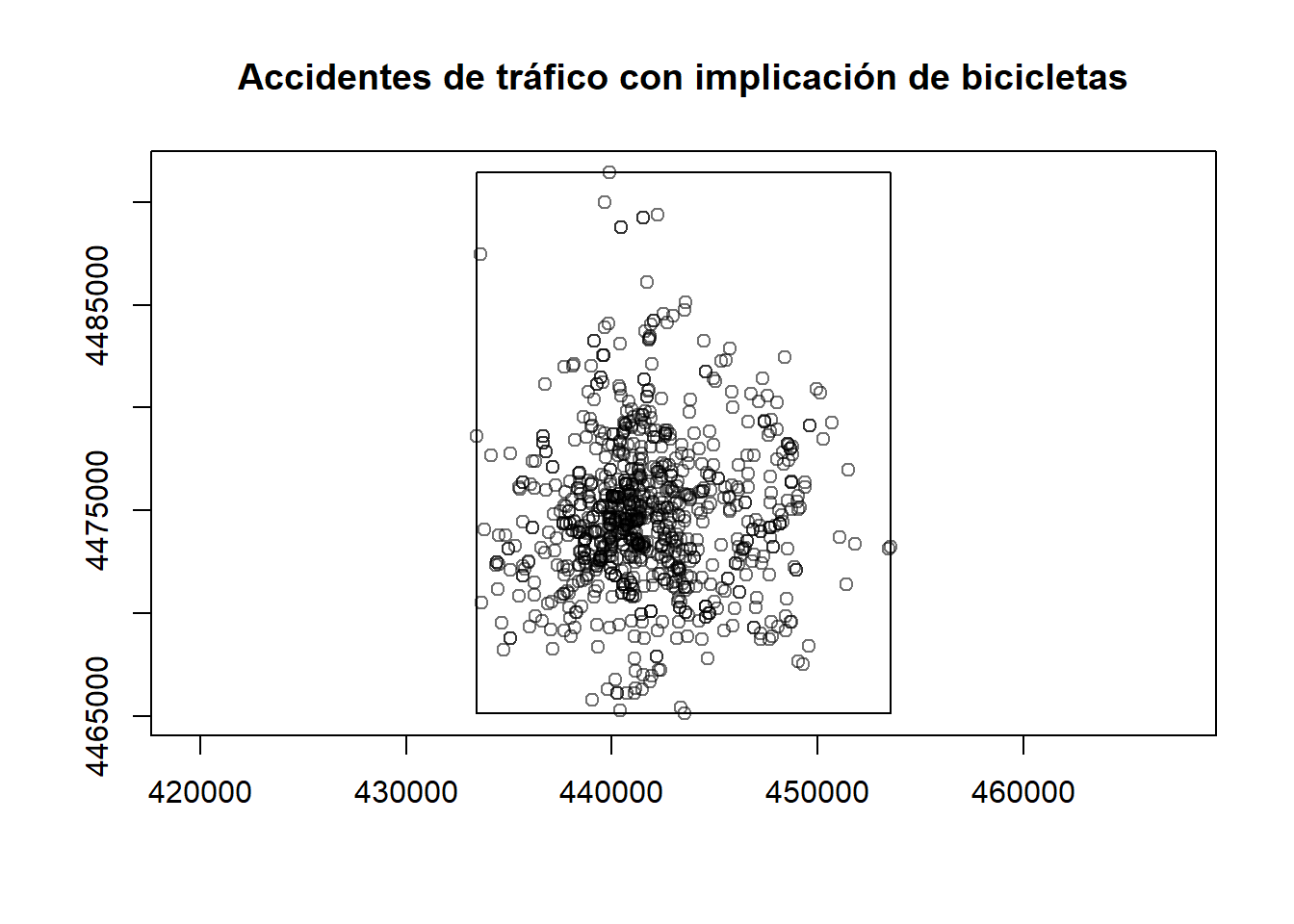
Comprobemos ahora si existe o no aleatoriedad espacial completa (CSR):
env_bici <- envelope(bici_ppp, fun=Gest, nsim=100, nrank=2, verbose = F)
plot(env_bici, main="Entorno de Confianza para 'bici_23'")
Puesto que rechazamos CSR, podemos afirmar que existe algún tipo de relación entre las localizaciones.
Otra forma de evaluar la aleatoriedad espacial es mediante la K de Ripley. Como se puede observar, existe una notable diferencia entre el trazo teórico (Poisson) y las estimaciones basadas en los métodos iso (Ripley’s isotropic correction), trans (Translation correction) y bord (border method or “reduced sample” estimator).
K <- Kest(bici_ppp)
plot(K)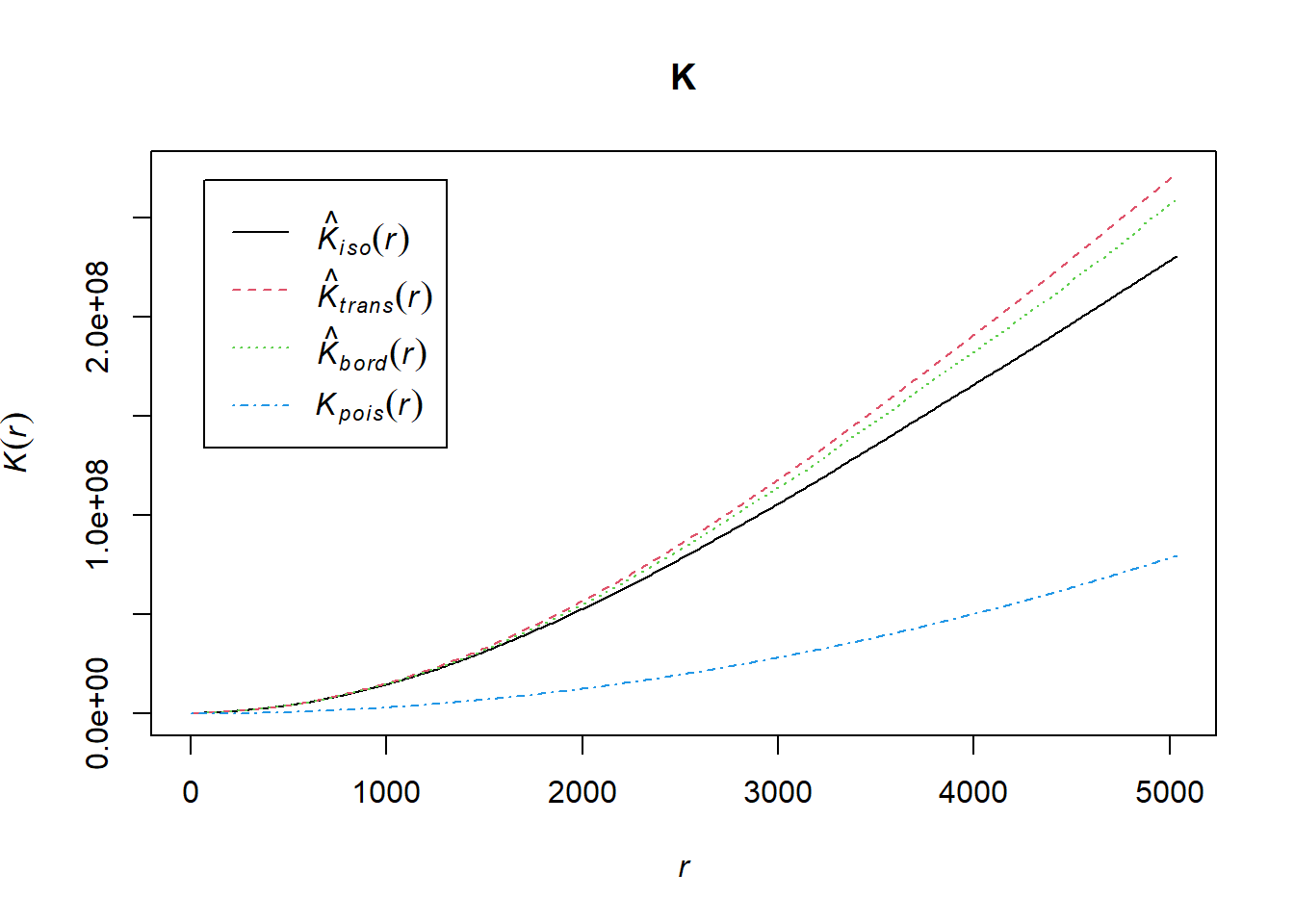
Para analizar la agrupación, podemos utilizar el análisis de clúster, como DBSCAN (Jörg Sander et al., 1998). Este método está disponible para aplicar directamente a objetos sf usando el paquete dbscan(Hahsler et al., 2019; Hahsler y Piekenbrock, 2022). Sin embargo, para mantenernos dentro de la esfera de spatstat, usaremos la L de Ripley (una transformación de la K que estabiliza la varianza y hace que los resultados visuales sean más interpretables). Para ello usaremos la función Lest():
L <- Lest(bici_ppp)
plot(L)
Para observar la densidad, replicaremos los gráficos anteriores. Primero en 3D:
poli <- as.points(list(x=c(rep(min(xrange),2),rep(max(xrange),2)),
y=c(min(yrange),rep(max(yrange),2),min(yrange))))
G <- Gest(bici_ppp)
max(G$r)[1] 1464.749suavizados <- mse2d(pts = as.points(bici_ppp),
poly = poli,
nsmse = 100,
range = 1500)
suavizados$h[which.min(suavizados$mse)][1] 315b <- kernel2d(pts = as.points(bici_ppp),
poly = poli,
h0 = 315)Xrange is 433418.1 453559.6
Yrange is 4465121 4491426
Doing quartic kernelb1 <- b$x
b2 <- b$y
b3 <- b$zpar(mar=c(2,2,1,2))
persp(b1, b2, b3,
theta = 45, phi = 30, ltheta = 120, shade = 0.75,
expand = 0.5, col = "aquamarine", ticktype="detailed",
xlab = "", ylab = "", zlab = "", main = "Intensidad")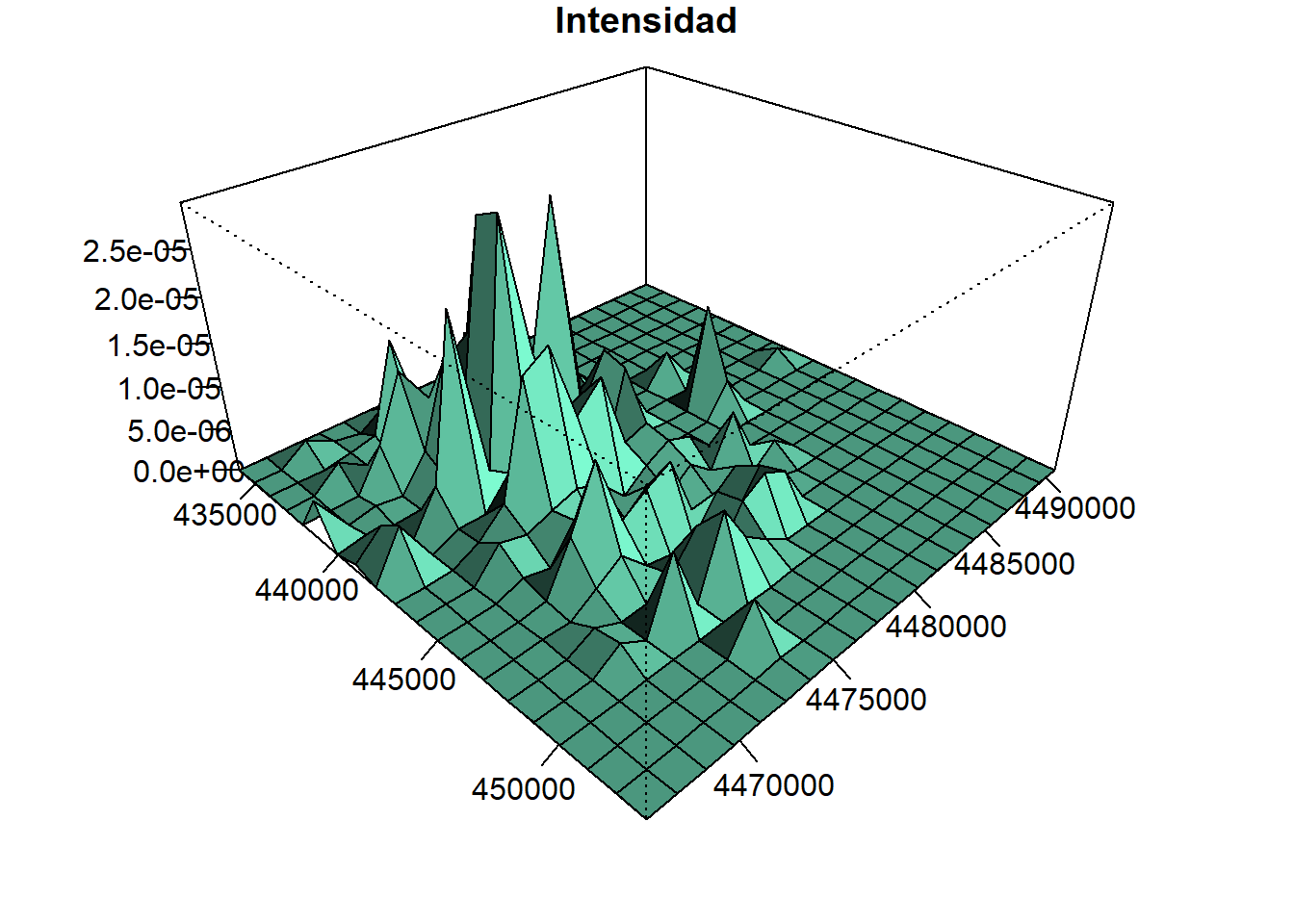
Gráfico de densidad en 2D:
densidad <- density.ppp(bici_ppp, sigma = bw.diggle)
par(mar = c(2,2,1,2))
plot(densidad)
Gráfico con ggplot2:
densidad_df <- as.data.frame(densidad)
names(densidad_df) <- c("x", "y", "densidad")
madrid <- mapSpain::esp_get_munic() %>% filter(name == "Madrid")
madrid <- sf::st_transform(madrid, crs=25830)options(scipen = 999)
ggplot() +
geom_tile(data = densidad_df, aes(x = x, y = y, fill = densidad)) +
geom_sf(data = madrid, fill=NA, color="black") +
scale_fill_gradient(low = "white", high = "red",
guide = guide_colourbar(barwidth = 20,
barheight = 0.5,
direction = "horizontal")) +
theme_void() +
theme(legend.position = "bottom",
legend.key.width = unit(1, "cm"),
legend.key.height = unit(0.5, "cm"),
legend.title = element_blank(),
legend.box = "horizontal")
La función addHeatmap del paquete leaflet.extras(Gatscha et al., 2024) también permite incluir un mapa de densidad:
bici_23_sf <- sf::st_transform(bici_23_sf, 4326)
bici_23_sf %>%
leaflet::leaflet() %>%
leaflet::addTiles() %>%
leaflet::addCircles(radius = 2, color = 'black', fillOpacity = 0.5) %>%
leaflet.extras::addHeatmap(intensity = 1, radius = 15, blur = 15, max = 0.5)