2 Análisis de datos espaciales
El análisis de datos espaciales representa un campo fundamental en la comprensión y manejo de información geográfica, permitiendo a los investigadores y profesionales descubrir patrones, correlaciones y tendencias subyacentes en datos que varían en función de su ubicación geográfica. Este tipo de análisis se ha vuelto indispensable en diversas áreas como la planificación urbana, la gestión ambiental, la epidemiología o la logística, entre otras, proporcionando información valiosa y permitiendo entender mejor los patrones, las dinámicas y las interacciones que ocurren en el espacio geográfico. A través de métodos y técnicas especializadas, este análisis permite descubrir correlaciones, tendencias y anomalías espaciales, facilitando la toma de decisiones basada en la comprensión profunda del espacio y sus componentes. Dentro del análisis de datos espaciales, se pueden distinguir tres áreas clave: las técnicas descriptivas que resumen la información, la visualización que traduce los datos en representaciones gráficas y la exploración espacial que identifica relaciones y patrones subyacentes.
2.1 Técnicas de análisis descriptivo
La información espacial es susceptible de ser analizada estadísticamente como cualquier otro tipo de información. Una serie de \(n\) datos recogidos en otros tantos puntos no deja de ser una serie de datos sobre la que pueden aplicarse las técnicas estadísticas habituales. Junto a ello, cada uno de estos datos tiene asociada una coordenada, y esta aporta una información adicional que puede emplearse igualmente para obtener resultados estadísticos de diversa índole.
Si trabajamos en el plano cartesiano \((x,y)\) en lugar de una serie de valores de una variable \(a\) disponemos de una serie de ternas \((x,y,a)\). Extendiendo la posibilidad de analizar estadísticamente los valores \(a\) recogidos en esa serie de localizaciones, encontramos otras dos formas de analizar este conjunto.
- Analizar la disposición espacial, con independencia de los valores. Es decir, estudiar el conjunto de pares de valores \((x,y)\)
- Analizar la disposición espacial y los valores recogidos. Es decir, estudiar el conjunto de ternas \((x,y,a)\)
Este tipo de análisis se lleva a cabo preferentemente sobre capas de tipo vectorial, aunque algunas de estas formulaciones pueden igualmente aplicarse a capas de tipo raster, considerando que cada celda conforma de igual modo una terna de valores.
En este apartado introduciremos algunos de los análisis estadísticos espaciales más básicos, como son los siguientes:
- Medidas centrográficas. El equivalente espacial de las medidas de tendencia central como el momento de primer orden (media) o la mediana, así como de las de dispersión tales como el momento de segundo orden (desviación típica).
- Análisis estadístico de líneas. Descriptores estadísticos para líneas y ángulos.
- Análisis de patrones de puntos. Este tipo de análisis permite caracterizar la estructura espacial de un conjunto de puntos en función de parámetros como la densidad o las distancias entre puntos y su configuración en el espacio.
- Autocorrelación espacial. Como ya comentamos anteriormente, los puntos cercanos tienden a tener valores más similares entre sí que los puntos alejados. Este fenómeno puede cuantificarse y estudiarse con una serie de índices u otros elementos tales como variogramas o correlogramas.
2.1.1 Medidas centrográficas
Al igual que la estadística descriptiva ha desarrollado un conjunto de medidas de centralidad y dispersión, en el marco del análisis estadístico de datos espaciales contamos con un conjunto de medidas análogas aplicado a la localización de conjuntos de datos.
Habitualmente, estas medidas centrográficas no permiten obtener un gran detalle o profundidad en la descripción de conjuntos de datos espaciales. Así pues, estas medidas suelen emplearse para comparar aspectos generales relativos a la distribución espacial de varios conjuntos de datos. Por ejemplo, la distribución de población de diferentes grupos sociales, la evolución temporal de la ocurrencia de un determinado evento, etc.
Las medidas que revisaremos a continuación se aplican, en su mayoría, a conjuntos de datos espaciales de tipo vectorial.
2.1.1.1 Medidas de centalidad
Las medidas de centralidad comprenden un conjunto de descriptores básicos de los datos espaciales que ofrecen un resumen sencillo de una distribución espacial. Estas medidas equivalen a los tradicionales descriptores de centralidad. Identificamos en este grupo las medidas siguientes:
Centro medio. Punto cuyas coordenadas han sido obtenidas mediante el cálculo de la media de los valores de las coordenadas para los ejes \(x\) e \(y\) de un conjunto de puntos. Expresamos el centro medio \((\overline{x}, \overline{y})\) para un conjunto de puntos \((x_{i},y_{i})\) como:
Algunas propiedades adicionales del centro medio son las siguientes:
- La suma del cuadrado de la distancias entre el centro medio y cada uno de los puntos es mínima.
- La suma de las diferencias entre el valor de la coordenada \(x\) del centro medio y los valores de la coordenada \(x\) del resto de puntos es 0 (y lo mismo ocurre para la coordenada \(y\)).
- La suma del cuadrado de la distancias entre el centro medio y cada uno de los puntos es mínima.
- Centro medio ponderado. Si aplicamos al cálculo del centro medio una ponderación dependiente de una variable asociada a cada punto, obtendremos el centro medio ponderado. Por ejemplo, mientras que el centro medio de un grupo de tiendas de comestibles sería la ubicación obtenida mediante una media de las coordenadas \(x\) e \(y\) de las tiendas, el centro medio ponderado estaría más cerca de las tiendas con mayor número de ventas, más metros cuadrados, o con mayor cantidad de algún otro atributo especificado.
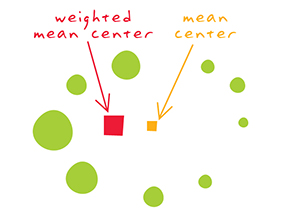
Centro mediano. También se denomina centro de distancia mínima y es el equivalente espacial de la mediana. Es aquel punto del espacio que minimiza la suma de las distancias a todos los puntos de un conjunto dado.
Geográficamente podemos definir el centro mediano como el punto de cruce de dos rectas perpendiculares entre sí, cada una de las cuales divide una población de \(n\) puntos en dos conjuntos de \(n/2\) puntos:
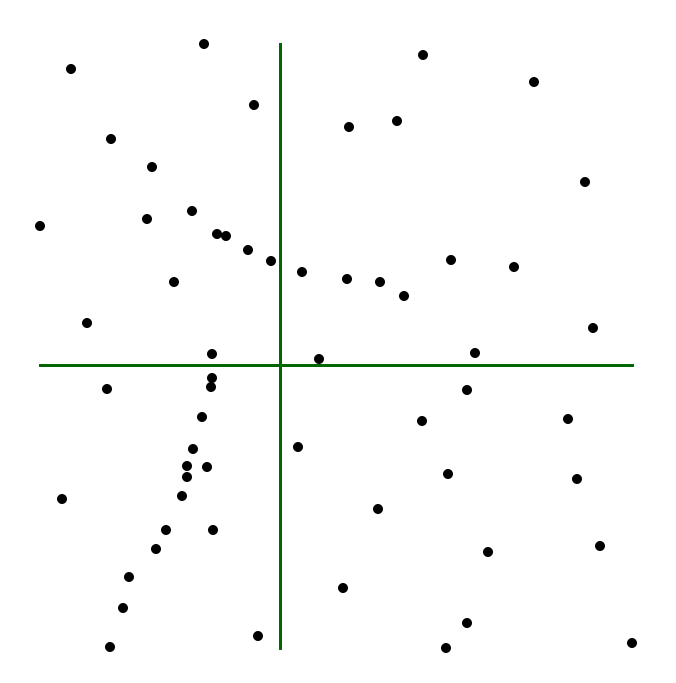
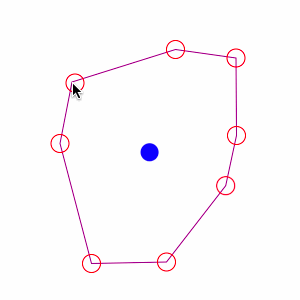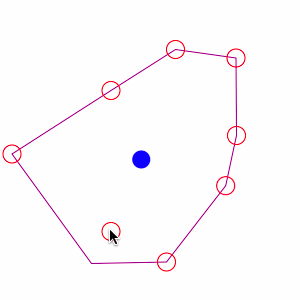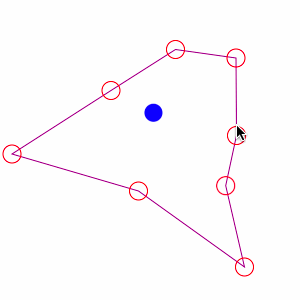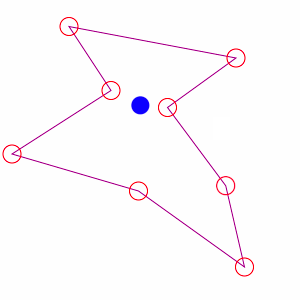
Centroide. El centroide de un polígono es el punto medio o centro de masas del mismo. Equivale al centro medio del conjunto de vértices que definen un polígono.
Hay que tener en cuenta que el centroide no tiene que estar obligatoriamente situado dentro del polígono. En ocasiones, se utilizan los centroides de un conjunto de polígonos para poder aplicar medidas centrográficas sobre los mismos.
2.1.1.2 Medidas de dispersión
Este conjunto de medidas nos permiten cuantificar la dispersión de un conjunto de datos en relación con su centro medio. En este apartado abordaremos la distancia típica y la elipse de desviación estándar:
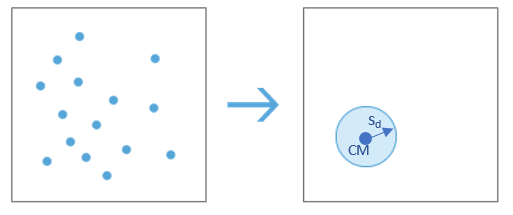
- Distancia típica. Representa la desviación estándar de la distancia entre los puntos y el centro medio. Es el equivalente bidimensional de la desviación estándar en variables simples. Podemos calcular su valor mediante la fórmula siguiente: \[s_d=\sqrt{\frac{\sum^n_{i=1}d^2_i}{n}}\] Esencialmente, representa la distancia media entre cada punto de un conjunto y su centro medio. Habitualmente, representamos esta medida como un círculo, con centro en el centro medio, cuyo radio es el valor calculado para la desviación típica.
En la siguiente imagen se ofrece el punto medio y el círculo de una desviación típica de distancias del mapa de observatorios meteorológicos de la cuenca del Segura.
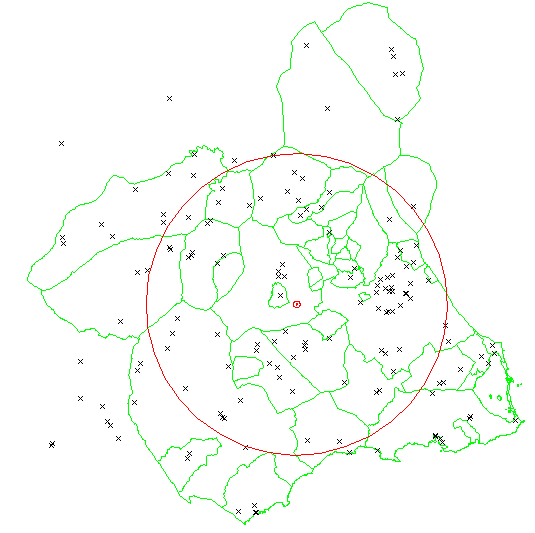
¿En qué otras situaciones podrían tener una imagen similar a esta?
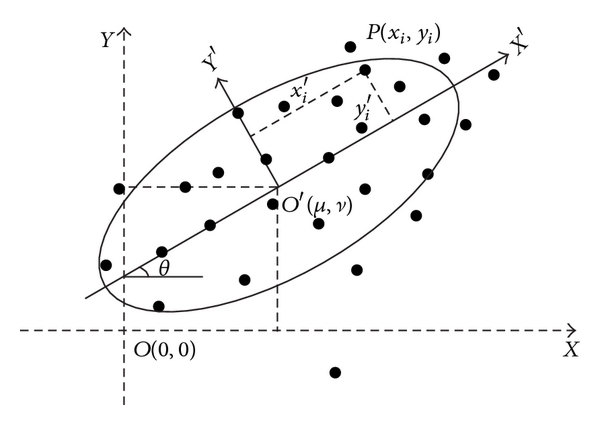
- Elipse de desviación estándar. La distancia típica es un buen indicador de la dispersión de un conjunto de puntos alrededor del centro medio. Sin embargo, no es útil para identificar la existencia de una orientación particular o sesgo direccional en los datos. Precisamente, la elipse de desviación estándar nos permite obtener una medida de la dispersión en dos direcciones. La elipse viene definida por tres parámetros:
- el ángulo de rotación \(\theta\)
- la dispersión a lo largo del eje mayor \(x’\)
- la dispersión a lo largo del eje menor \(y’\)
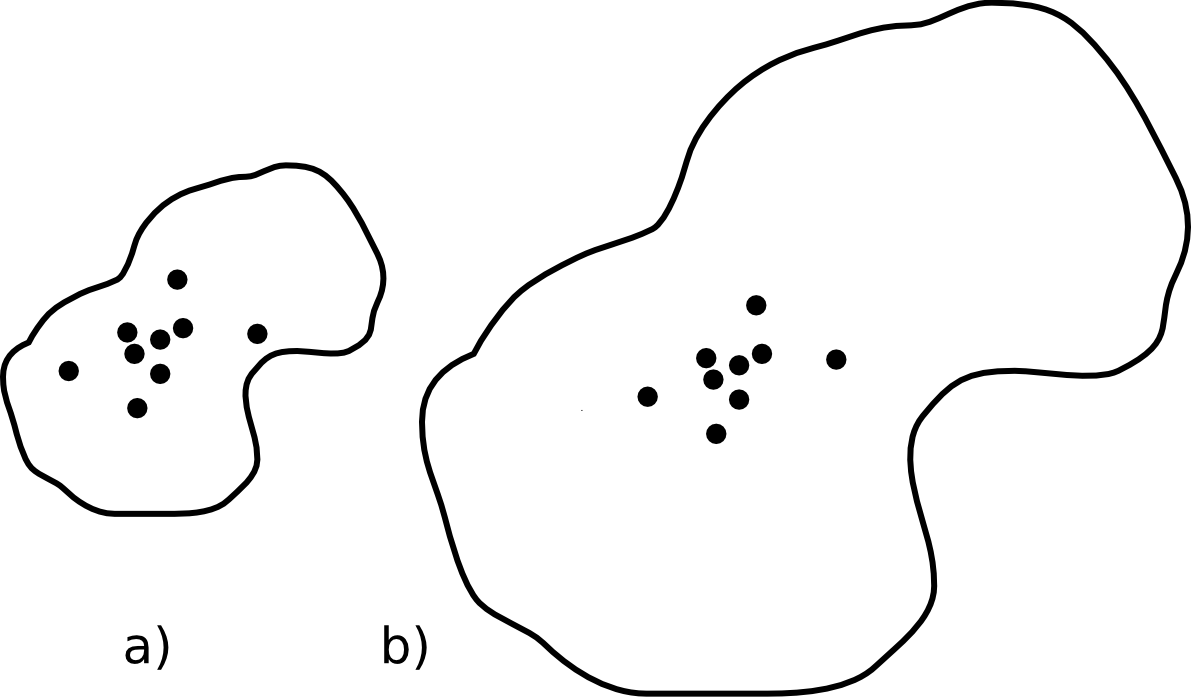
Distancia relativa. Es la medida de dispersión relativa que equivale en la estadística espacial al coeficiente de variación, y se calcula dividiendo la distancia típica por el radio de un círculo con el mismo área que la zona de estudio.
Si esta zona es circular, se tiene que \(s_{d,rel} = \frac{s_d}{R}\)
En caso de que esta zona fuera cuadrada, y de área \(A\), se tiene que \(s_{d,rel} = \frac{s_d\sqrt{\pi}}{\sqrt{A}}\)
En la figura puede verse cómo distribuciones espaciales iguales (con la misma distancia típica) representan dispersiones relativas distintas en relación a la zona de estudio.
2.1.2 Análisis estadístico de líneas
Dentro de los objetos geográficos, las líneas merecen algunos comentarios aparte en lo que a su análisis respecta. Como hemos visto, tanto las líneas como los polígonos pueden ser reducidos en ultima instancia a puntos y ser analizados con algunas de las fórmulas vistas anteriormente. La particularidad de las líneas estriba en que, además de valores puntuales o de área (como los de los polígonos), definen igualmente direcciones y ángulos de giro entre sus segmentos. El análisis estadístico de variables circulares como estas presenta sus propias particularidades, que deben conocerse para poder extraer resultados correctos a partir de datos de esta índole.
Un ejemplo del uso de variables direccionales lo encontramos, por ejemplo, en el estudio de desplazamientos de animales cuyas rutas hayan sido monitorizadas y se encuentren dentro de un SIG como capas de líneas. Un situación similar se da en el caso de elementos que no representen un movimiento pero tengan dirección, tales como fallas u otros elementos geológicos. Más allá de casos como estos, los conceptos relativos a este tipo de variables también tienen aplicación para cualquier información similar, con independencia de su formato de almacenamiento. Así, son de aplicación, entre otros, para el estudio de orientaciones dentro del análisis geomorfométrico, el cual se lleva a cabo fundamentalmente sobre capas raster.
En cualquier caso, pueden considerarse todos y cada uno de los segmentos de estas como líneas en sí, o bien la línea ficticia que une el inicio del primer segmento con el final del último.
2.1.3 Estadísticos para datos circulares
El cálculo de la media de dos ángulos ejemplifica bien las particularidades de los datos circulares. Sean tres ángulos de \(5°\), \(10°\) y \(15°\) respectivamente. El concepto habitual de media aplicado a estos valores resultaría en un ángulo medio de \(10°\), correcto en este caso. Si giramos ese conjunto de ángulos 10 grados en sentido antihorario, dejándolos como \(355°\), \(0°\), \(5°\), la media debería ser \(0°\), pero en su lugar se tiene un valor medio de \(120°\).
Una forma correcta de operar con ángulos \(\alpha_1,…,\alpha_n\) consiste en hacerlo con las proyecciones del vector unitario según dichos ángulos, es decir \(\sin{\alpha_1},….\sin{\alpha_n}\) y \(\cos{\alpha_1},….\cos{\alpha_n}\). Aplicando luego los estadísticos habituales sobre estos valores se obtienen unos nuevos valores de senos y cosenos que permiten obtener el ángulo resultante aplicando sobre ellos la función arcotangente.
En el caso de segmentos orientados, tales como los que constituyen las líneas dentro de una capa de un SIG, resulta conveniente tratar cada segmento como un vector. La resultante de su suma vectorial será otro vector con la dirección media de todos los segmentos, y cuyo módulo (longitud) aporta información acerca de la tendencia y variación de las direcciones a lo largo de la linea. Si la dirección es uniforme, el módulo será mayor, siendo menor si no lo es. El vector resultante puede dividirse por el número total de segmentos iniciales para obtener una media vectorial:

Es decir, se tiene un vector cuya orientación viene definida por un ángulo \(\alpha\) tal que \(\alpha = \arctan{\frac{S}C}\) y con un módulo \(\overline{R}\) según \(\overline{R} = \frac{\sqrt{S^2 + C^2}}N\) siendo \(S\) y \(C\) las sumas de senos y cosenos, respectivamente:
\[S = \sum_{i=1}^N \sin{\alpha_i} \qquad \qquad C = \sum_{i=1}^N \cos{\alpha_i}\] El módulo \(\overline{R}\) se conoce también como concentración angular y es una medida inversa de la dispersión angular. No obstante, hay que tener en cuenta que valores próximos a cero, los cuales indicarían gran dispersión, pueden proceder de dos agrupaciones de ángulos similares (es decir, con poca dispersión) si estas agrupaciones se diferencian entre sí \(180°\).
La forma en que las distintas orientaciones se congregan en torno a la media, relacionada directamente con la dispersión, puede servir para inferir la existencia de una dirección predominante o bien que los valores angulares se hallan uniformemente distribuidos. La comprobación de que existe una tendencia direccional es de interés para el estudio de muchos procesos tales como el estudio de movimiento de individuos de una especie, que puede denotar la existencia de una línea migratoria preferida o revelar la presencia de algún factor que causa dicha predominancia en las direcciones.
Existen diversos test que permiten aceptar o rechazar la hipótesis de existencia de uniformidad, entre los cuales destacan el test de Rayleigh, el test V de Kuiper o el test de espaciamiento de Rao. Para este último, se tiene un estadístico \(U\) según
\[U = \frac{1}2\sum_{i=1}^N \|T_i - \lambda\|\]
Puesto que las desviaciones positivas deben ser iguales a las negativas, lo anterior puede simplificarse como
\[\begin{equation} U = \sum_{i=1}^N (T_i - \lambda) \end{equation}\]
Para un numero de puntos dado y un intervalo de confianza establecido, los valores de \(U\) están tabulados, y puede así rechazarse o aceptarse la hipótesis nula de uniformidad. Dichas tablas pueden encontrarse, por ejemplo, aquí.
2.2 Visualización de datos espaciales
La correcta representación de datos espaciales es fundamental para visualizar patrones geográficos de manera clara y comprensible. Para que una visualización sea efectiva, es más que recomendable seguir ciertos principios que garanticen precisión, accesibilidad y utilidad en la toma de decisiones. En este apartado se presentan, por un lado, los principales aspectos a considerar en la visualización de datos espaciales y, por otro lado, diferentes tipos de visualización. También se presentan algunas herramientas para la visualización de datos espaciales y espaciotemporales así como diversas aplicaciones en el ámbito de la inteligencia de negocios.
2.2.1 Principios básicos de la visualización espacial
La visualización espacial es una herramienta fundamental para representar datos geográficos y patrones espaciales de manera clara y comprensible. Para que una visualización sea efectiva, debe seguir ciertos principios que garanticen su precisión, accesibilidad y utilidad en la toma de decisiones. A continuación, se presentan los principales principios a considerar:
Legibilidad: La información debe ser fácilmente comprensible para el usuario. Esto implica el uso de etiquetas claras, una tipografía adecuada y una disposición visual que permita una interpretación rápida de los datos. Un mapa desordenado o con demasiados elementos superpuestos puede dificultar su comprensión y restarle efectividad.
Simplicidad: Una visualización efectiva debe evitar la sobrecarga visual. La inclusión excesiva de elementos gráficos, colores o detalles innecesarios puede generar confusión y hacer que el mensaje principal se pierda. Es recomendable mantener un diseño limpio, con una cantidad equilibrada de información que permita resaltar los aspectos clave sin distraer al usuario.
Exactitud: La representación de los datos debe reflejar fielmente la realidad espacial y las relaciones entre los elementos geográficos. Esto incluye el uso correcto de escalas, la adecuada georreferenciación de los datos y la minimización de distorsiones. Una visualización inexacta puede llevar a interpretaciones erróneas y afectar la validez del análisis.
Consistencia: Es fundamental mantener un uso uniforme de colores, símbolos y escalas en todas las visualizaciones dentro de un mismo proyecto o conjunto de datos. La coherencia gráfica facilita la comparación entre diferentes mapas o gráficos espaciales, evitando confusiones y ayudando a establecer una narrativa visual clara.
Además de estos principios, es importante considerar el público objetivo al diseñar una visualización espacial. Dependiendo del nivel de conocimiento del usuario final, se pueden ajustar aspectos como el nivel de detalle, la paleta de colores o la inclusión de explicaciones adicionales para mejorar la accesibilidad de los datos.
2.2.2 Tipos de visualización de datos espaciales
Existen diversas formas de representar los datos espaciales, dependiendo de la naturaleza de la información y del objetivo del análisis. A continuación exploraremos algunas de las más habituales.
2.2.2.1 Mapas coropléticos (choropleth maps)
Los mapas de coropletas representan datos cuantitativos mediante una escala de colores aplicada a áreas geográficas, permitiendo identificar patrones espaciales y comparaciones entre regiones. En la Figura 2.1 se muestra la proporción de jóvenes de entre 15 y 29 años que ni estudian ni trabajan en los distintos países de Europa. Los países con porcentajes más altos están representados con tonos más oscuros, mientras que aquellos con menores tasas aparecen en tonos más claros. Este tipo de mapa permite identificar tendencias geográficas, como la concentración de este fenómeno en ciertas regiones, facilitando el análisis de políticas educativas y laborales a nivel continental.
2.2.2.2 Mapas de símbolos escalados
Los mapas de símbolos escalados son una alternativa a los mapas de coropletas para representar variables numéricas en un espacio geográfico. En lugar de utilizar colores para indicar valores dentro de áreas geográficas, estos mapas emplean símbolos de distinto tamaño para codificar la magnitud de una variable.
Los símbolos pueden ubicarse en puntos exactos, cuando se dispone de coordenadas precisas, o dentro de polígonos que representan áreas geográficas, como países o regiones, cuando se trabaja con datos agregados. El tipo de símbolo más utilizado en estos mapas es el círculo, ya que permite una comparación visual intuitiva entre los valores representados. Es importante que la superficie del círculo sea proporcional a la variable que representa, evitando que la percepción del tamaño genere interpretaciones erróneas.
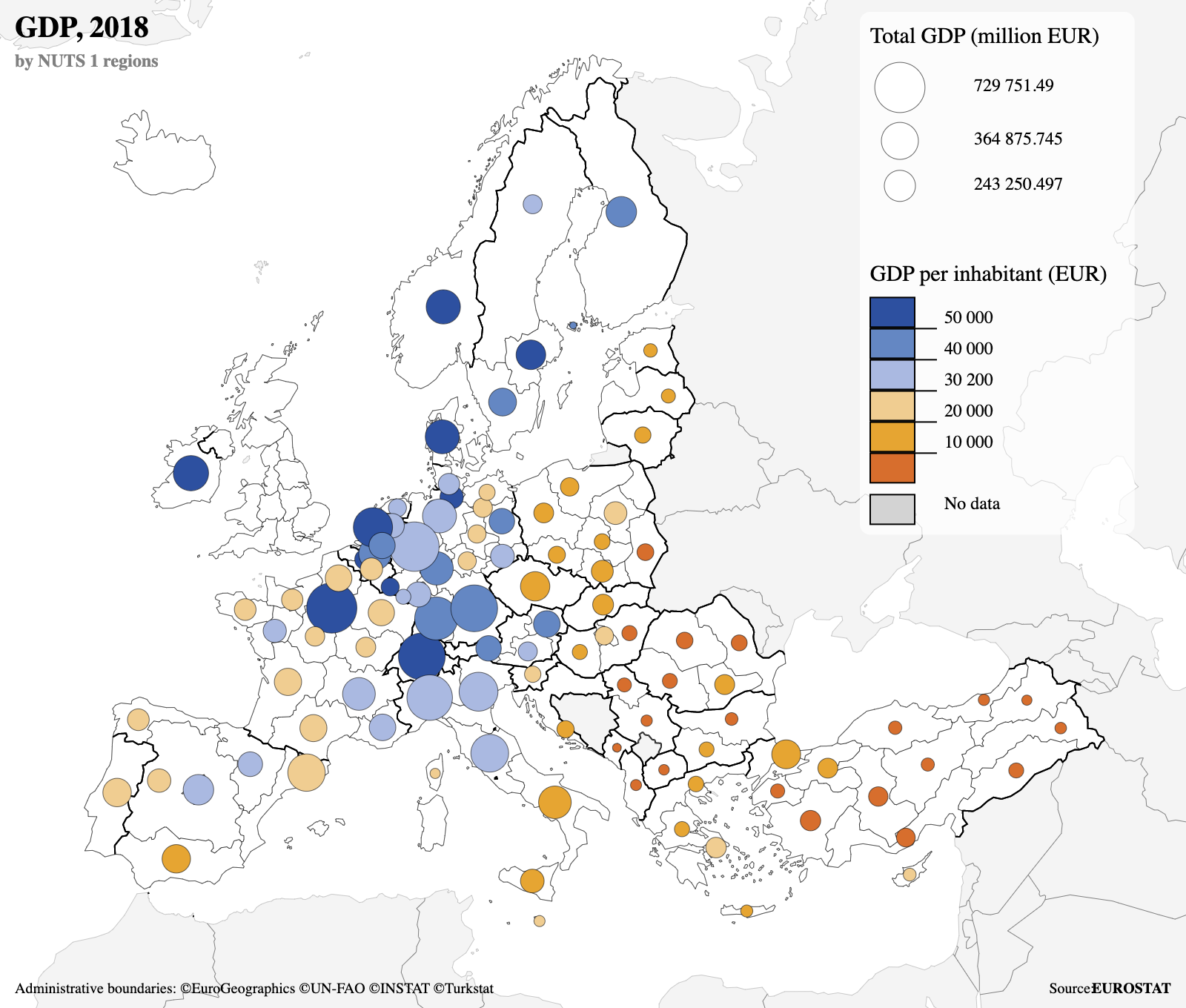
En la Figura 2.2, además del tamaño de los círculos para representar una variable principal (PIB total de la región), el color de cada círculo se ha utilizado para codificar una segunda variable numérica (PIB per cápita), permitiendo visualizar dos dimensiones de los datos en una sola representación.
2.2.2.3 Mapas de puntos
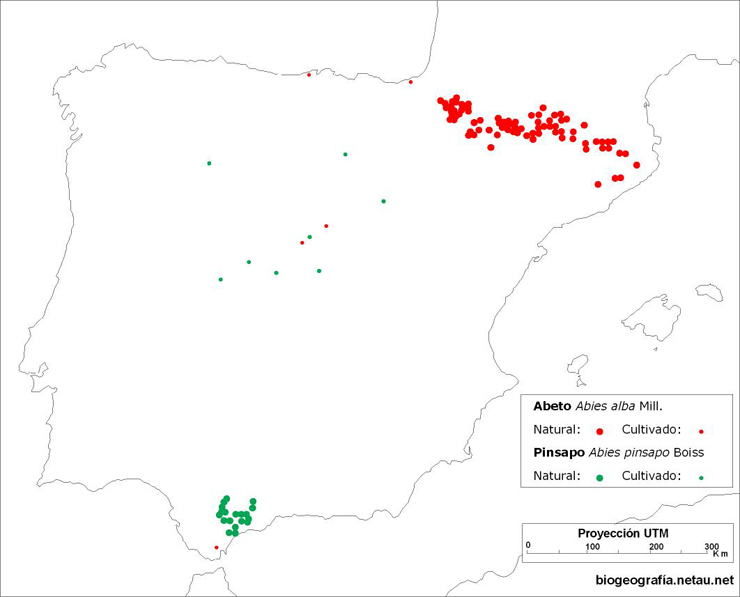
Los mapas de puntos se utilizan para representar la distribución geográfica de elementos individuales dentro de un área determinada. Cada punto en el mapa corresponde a una ubicación específica de un fenómeno, permitiendo observar patrones de concentración, dispersión o ausencia de ciertos elementos. En la Figura 2.3 se muestra la ubicación de dos tipos de árboles en España, diferenciados por color para facilitar su identificación. Este enfoque permite comparar la distribución de ambas especies y detectar posibles patrones ecológicos o climáticos que influyen en su presencia. Los mapas de puntos son especialmente útiles en estudios de biodiversidad, demografía o eventos geolocalizados, ya que ofrecen una representación detallada y precisa de los datos espaciales.
2.2.2.4 Mapas de calor (heatmaps)
Una variante de los mapas de puntos es el heatmap o mapa de calor, que permite visualizar la densidad de puntos en una región mediante una escala de colores. En lugar de mostrar cada punto individualmente, los heatmaps representan la concentración de elementos con gradientes de color, donde las áreas con mayor densidad suelen aparecer en tonos más intensos (como rojo o naranja) y las de menor concentración en tonos más suaves (como azul o verde).
Este tipo de visualización es ampliamente utilizado en campos muy diversos. En estudios ambientales y de biodiversidad, los heatmaps ayudan a identificar zonas de alta presencia de especies, facilitando la planificación de conservación. En análisis urbanos, permiten detectar áreas con mayor tráfico peatonal o vehicular, siendo útiles para la planificación del transporte y la gestión del espacio público. También son empleados en epidemiología para mapear la propagación de enfermedades, en comercio para analizar la distribución geográfica de clientes y en seguridad ciudadana para identificar puntos con mayor incidencia de delitos o accidentes de tráfico, ayudando en la toma de decisiones para la prevención y la asignación de recursos.
2.2.2.5 Mapas de flujo (flow maps)
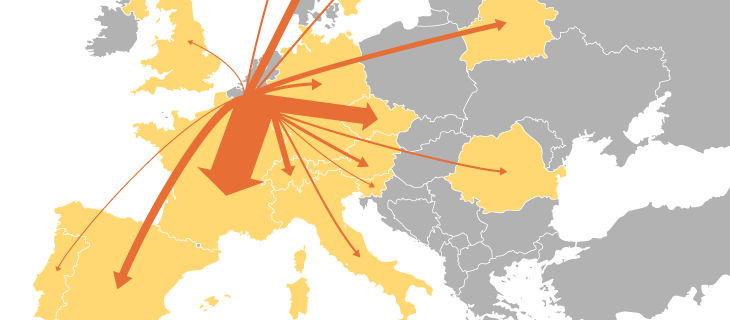
Los flow maps o mapas de flujo se utilizan para representar el movimiento de personas, bienes, información o cualquier otro tipo de flujo entre diferentes ubicaciones. Se caracterizan por el uso de líneas o flechas que conectan puntos en el mapa, donde el grosor, el color o la dirección de las líneas pueden codificar información sobre la cantidad y el sentido del flujo. Por ejemplo, un mapa de flujo puede mostrar la migración de población entre países, el transporte de mercancías entre ciudades o los patrones de tráfico en una región. Este tipo de visualización es especialmente útil para analizar tendencias espaciales y detectar patrones de conectividad, aunque debe diseñarse cuidadosamente para evitar la sobrecarga visual cuando hay múltiples rutas superpuestas.
2.2.2.6 Cartogramas
Los cartogramas son mapas en los que se altera la geografía para que la superficie de las entidades geográficas sea proporcional a un valor numérico (Tobler, 2004). A continuación, se presentan tres tipos principales de cartogramas con ejemplos visuales.
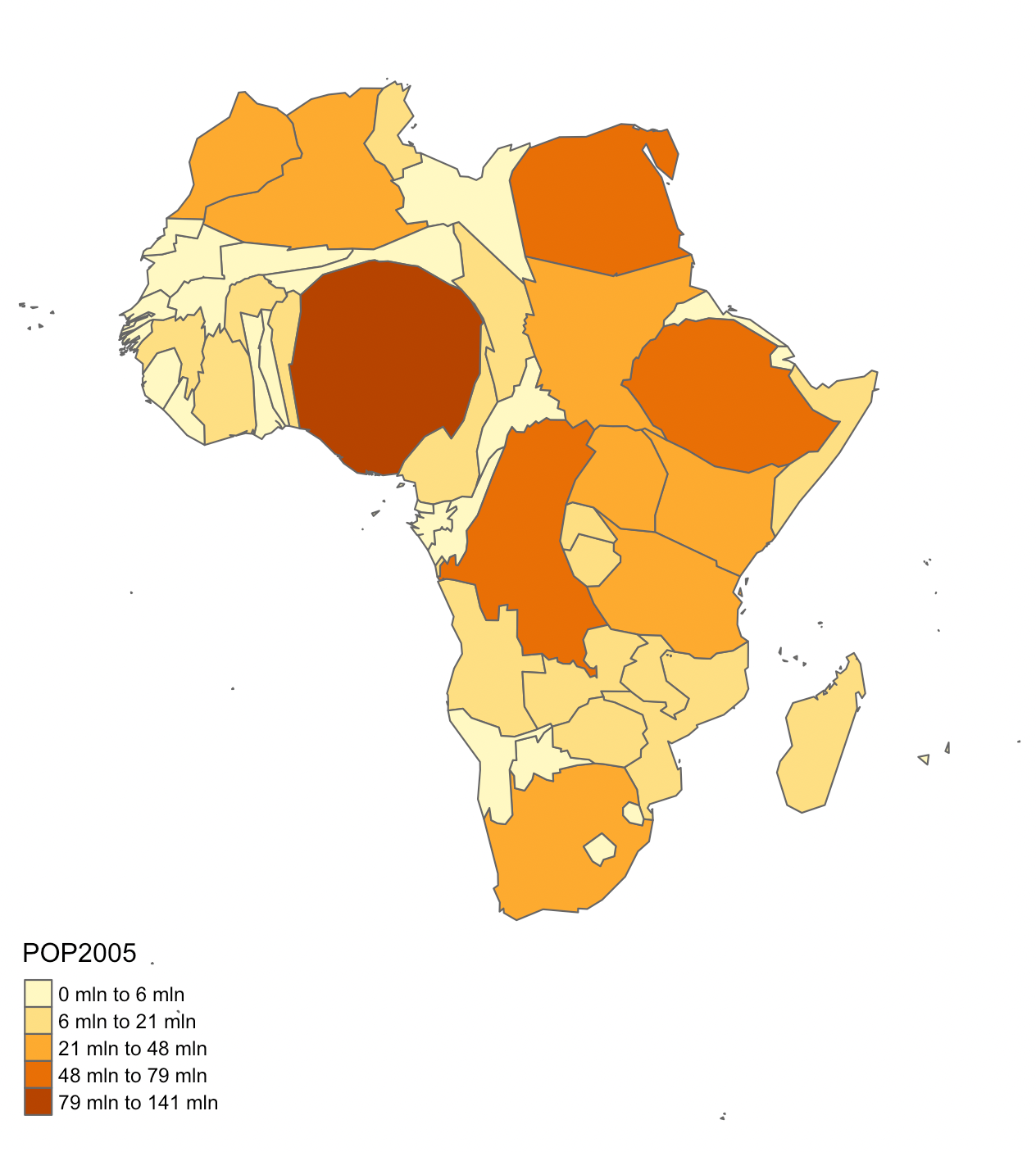
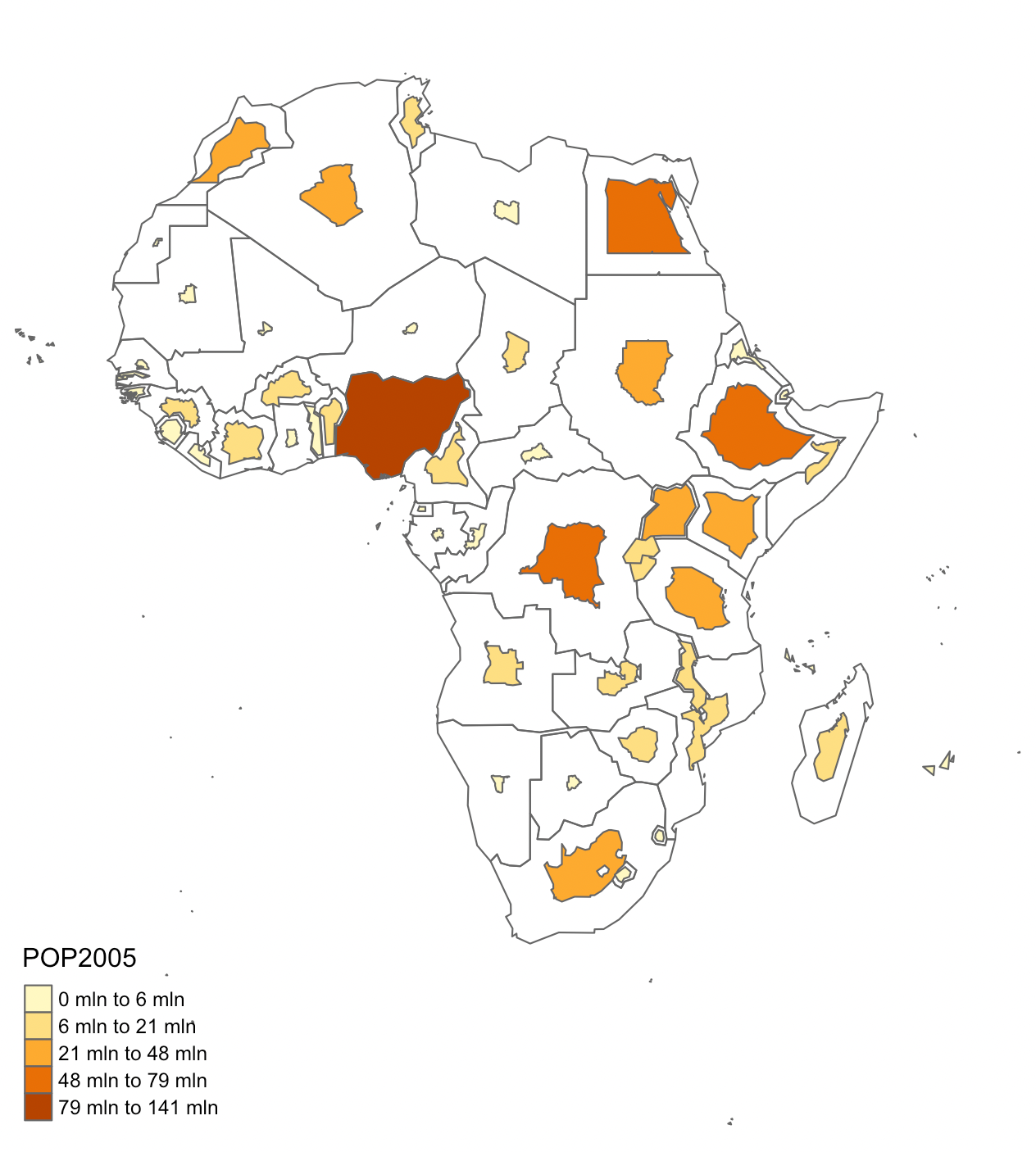
- En un cartograma contiguo, las entidades geográficas mantienen sus límites compartidos con los países vecinos, aunque su forma se distorsiona para reflejar el valor de la variable representada. En la Figura 2.6 se muestra la población total de los países africanos. En él, Nigeria, representada en rojo oscuro, aparece ampliada debido a su gran población, mientras que otros países se han reducido debido a sus menores poblaciones.
- En un cartograma no contiguo, las entidades se escalan para representar la variable en cuestión, pero ya no mantienen contacto entre sí. Esto permite que la distorsión sea más clara sin comprometer la legibilidad del mapa. Como se puede observar en la Figura 2.7 los países africanos han sido escalados según su población, lo que ha provocado que pierdan su continuidad geográfica.
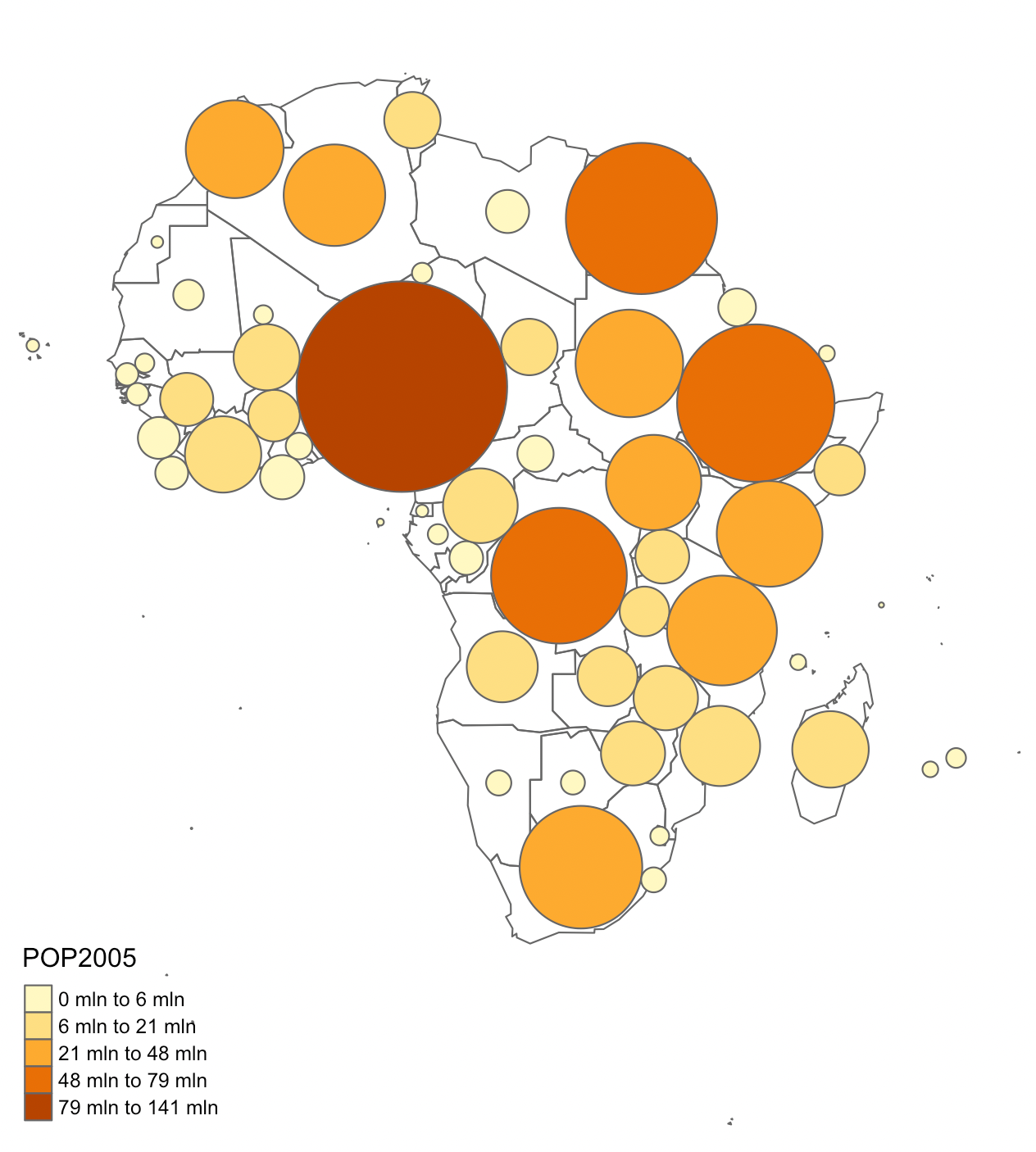
- En un cartograma de Dorling (Dorling, 2011), las formas originales de las entidades geográficas se reemplazan por círculos de tamaño proporcional al valor de la variable representada.
Un cartograma de Dorling es similar a un mapa de símbolos escalados, pero con una diferencia clave: en el cartograma de Dorling, los círculos suelen escalarse y posicionarse de manera que se toquen entre sí, pero nunca se superponen. En cambio, en los mapas de símbolos proporcionales, los círculos están más anclados a su ubicación geográfica original y pueden superponerse parcialmente.
En la Figura 2.8 se muestra un cartograma de Dorling en el que los países africanos han sido reemplazados por círculos de tamaño proporcional a su población, lo que permite una comparación visual más clara.
2.2.2.7 Mapas de agregación hexagonal (Hexbin maps)
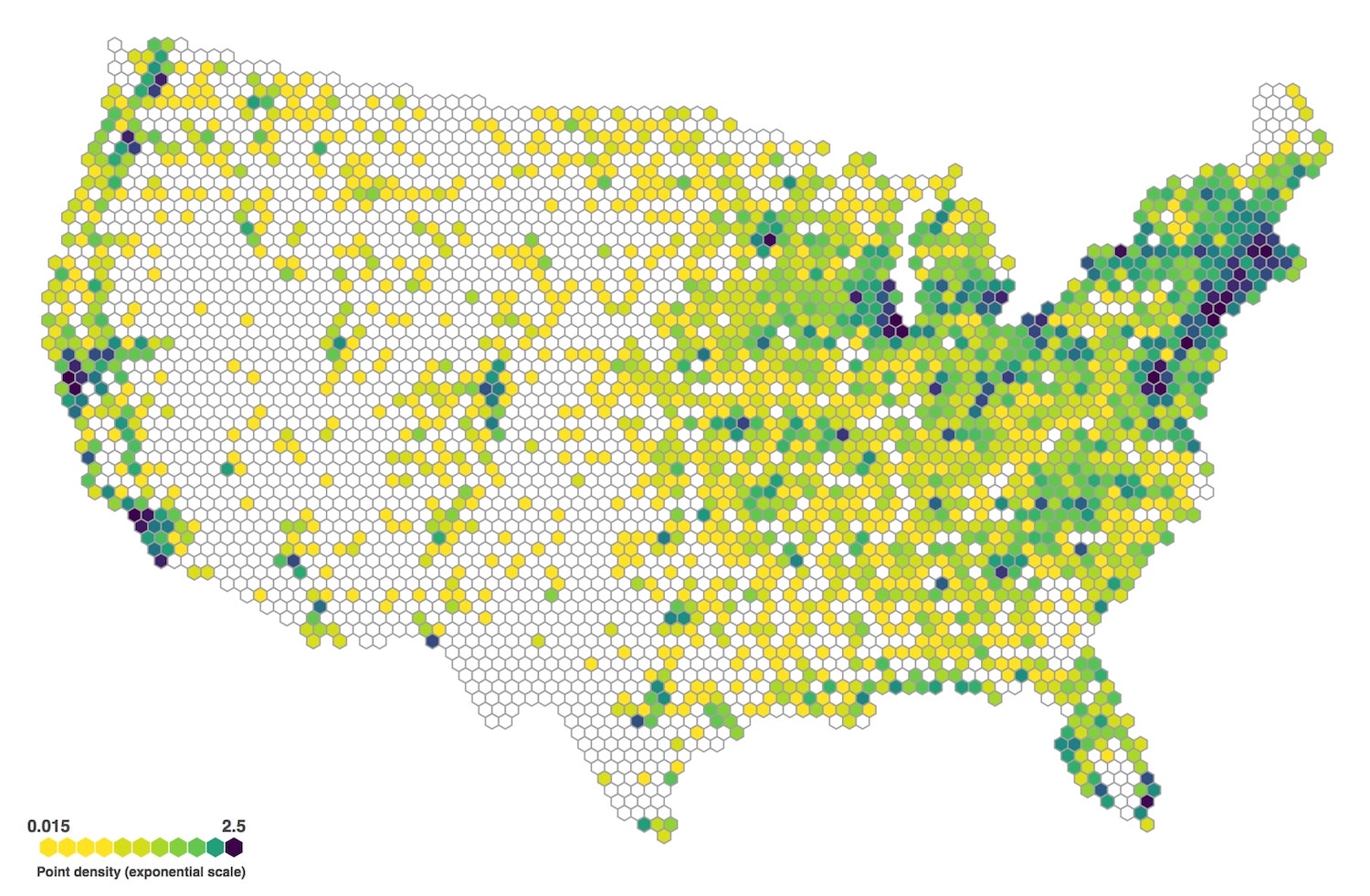
Un mapa con una gran cantidad de puntos puede representarse utilizando una cuadrícula (malla o grid) y contando cuántos puntos caen en cada celda. Si bien esta cuadrícula podría estar compuesta por cuadrados, generalmente se utilizan hexágonos porque cubren el plano de manera más eficiente y ofrecen una mejor visualización de los datos sin generar patrones de alineación artificiales. En la Figura 2.9 se muestra un Hexbin map con la densidad de mercados de agricultores en los Estados Unidos, donde la intensidad del color de cada hexágono representa la cantidad de mercados dentro de esa zona del territorio.
2.2.2.8 Visualizaciones dinámicas
Además de los mapas estáticos, existen herramientas interactivas que permiten explorar datos espaciales de manera más flexible y detallada. Las visualizaciones dinámicas permiten acercar, alejar, activar capas, desplegar información adicional al pasar el cursor o hacer clic sobre un elemento del mapa. Estas funcionalidades son especialmente útiles cuando se trabaja con grandes volúmenes de datos o cuando se busca mejorar la experiencia del usuario en la exploración de la información.
Tres de las bibliotecas más utilizadas para crear mapas interactivos son Leaflet, Mapbox y Maplibre.
Leaflet es una biblioteca de código abierto ligera y flexible que permite integrar mapas dinámicos en páginas web y aplicaciones. Es compatible con datos en formato GeoJSON, capas raster y vectoriales, y permite personalizar la visualización con iconos, marcadores y estilos personalizados. En R, Leaflet cuenta con un paquete dedicado (leaflet) que facilita la creación de mapas interactivos dentro del entorno de análisis. Dedicaremos una sesión práctica a conocer en profunidad esta librería.
Mapbox y Maplibre son más robustas y avanzadas, permitiendo la creación de visualizaciones interactivas altamente personalizables. Mapbox es una plataforma comercial que ofrece potentes herramientas para el diseño de mapas, integración con datos en tiempo real y renderizado 3D. Es ampliamente utilizada en aplicaciones móviles y web que requieren visualizaciones de alto rendimiento. Por otro lado, Maplibre es una bifurcación de código abierto de Mapbox GL JS, surgida tras la transición de Mapbox a un modelo más restrictivo. Esta biblioteca mantiene muchas de las capacidades avanzadas de Mapbox, como la renderización vectorial y la personalización mediante estilos JSON.
Además de estas bibliotecas, existen otras opciones como D3.js, que permite crear visualizaciones geoespaciales avanzadas mediante programación declarativa, o deck.gl, una biblioteca de alto rendimiento especializada en grandes volúmenes de datos geoespaciales.
La selección de la herramienta adecuada dependerá del caso de uso específico. Para aplicaciones web ligeras con mapas interactivos básicos, Leaflet es una excelente opción. Si se requiere renderizado 3D, integración con datos dinámicos o un alto nivel de personalización, Mapbox o Maplibre son alternativas más adecuadas. En escenarios donde se necesiten gráficos complejos o representación de datos geoespaciales a gran escala, D3.js o deck.gl pueden ser las mejores soluciones.
2.2.3 Herramientas para la visualización y análisis de datos espaciales
El análisis y la visualización de datos espaciales requieren herramientas especializadas que permitan gestionar, procesar y representar información georreferenciada de manera efectiva. Estas herramientas pueden agruparse en dos grandes categorías: Software de Sistemas de Información Geográfica (SIG) y plataformas de visualización en la web.
2.2.3.1 Software de Sistemas de Información Geográfica (SIG)
Los Sistemas de Información Geográfica (SIG) son herramientas diseñadas para la captura, almacenamiento, análisis y visualización de datos espaciales. Permiten manipular información en distintos formatos, realizar análisis geoespaciales avanzados y generar mapas con alto grado de personalización.
Algunas de las aplicaciones más utilizadas en este ámbito son:
- QGIS: Software de código abierto ampliamente utilizado en la comunidad geoespacial. Soporta múltiples formatos de datos, cuenta con una gran variedad de herramientas de análisis y permite la integración con lenguajes de programación como Python y R.
- ArcGIS: Una de las plataformas SIG más completas y utilizadas a nivel profesional. Desarrollada por Esri, ofrece herramientas avanzadas de análisis espacial, modelado geoespacial y visualización en 3D. Su ecosistema incluye ArcGIS Pro, ArcGIS Online y ArcGIS Enterprise.
- GRASS GIS: Un SIG de código abierto con potentes capacidades de análisis espacial, modelado y procesamiento de imágenes de teledetección. Es utilizado en proyectos de investigación y aplicaciones ambientales.
- SAGA GIS: Un SIG de código abierto con herramientas especializadas en análisis geomorfológico, modelado de terreno e hidrología. Se integra bien con R a través del paquete RSAGA, lo que permite acceder a su funcionalidad directamente desde el entorno de análisis.
Estos programas permiten la realización de operaciones como análisis de redes, interpolaciones espaciales, modelado de datos y generación de mapas temáticos. Son herramientas fundamentales para profesionales en geografía, urbanismo, medio ambiente y otras disciplinas que requieren análisis espaciales detallados.
2.2.3.2 Plataformas de visualización en la web
Además del software SIG tradicional, existen plataformas en la web que permiten la visualización e interacción con datos espaciales sin necesidad de instalar programas especializados. Estas herramientas han cobrado gran relevancia en los últimos años, facilitando la publicación de mapas interactivos y el acceso a datos geoespaciales en entornos colaborativos.
Algunas de las plataformas más destacadas son:
- Google Earth Engine: Un potente entorno basado en la nube que permite el análisis y visualización de imágenes satelitales y datos geoespaciales. Es ampliamente utilizado para estudios de cambio climático, monitorización ambiental y análisis de cobertura terrestre.
- ArcGIS Online: Versión en la nube de ArcGIS que permite la creación de mapas interactivos y dashboards sin necesidad de software instalado. Facilita la colaboración y el acceso a datos espaciales a través de la web.
- Carto: Plataforma enfocada en la visualización y análisis de datos espaciales con una interfaz intuitiva y herramientas avanzadas para análisis de datos geoespaciales. Es utilizada en sectores como transporte, planificación urbana y análisis de mercado.
- Kepler.gl: Herramienta de código abierto desarrollada por Uber para la visualización de grandes volúmenes de datos geoespaciales de manera eficiente y sin necesidad de programación.
El uso de estas herramientas web permite a los usuarios acceder y compartir información geoespacial de manera más accesible, integrándose con aplicaciones móviles, sistemas de monitoreo y otras tecnologías.
2.3 Exploración espacial de datos
La exploración espacial de datos constituye una fase fundamental en el análisis de información geográfica, ya que permite descubrir patrones, tendencias y relaciones en la distribución espacial de los fenómenos. Este apartado se centra en los métodos y técnicas que facilitan la comprensión inicial de los datos espaciales antes de aplicar modelos predictivos o inferenciales más complejos.
Entre los objetivos de la exploración espacial se encuentran los siguientes:
Identificación de patrones y clusters: Detectar agrupamientos, concentraciones y dispersión en la distribución de variables geográficas, lo que puede indicar la presencia de fenómenos subyacentes, como zonas de alta incidencia en problemas de salud, delitos o actividad económica.
Detección de valores atípicos (outliers): Localizar puntos que difieren significativamente del comportamiento general del conjunto de datos, ya que estos pueden representar errores en la recolección de datos o fenómenos excepcionales de interés.
Evaluación de la autocorrelación espacial: Analizar el grado en que las observaciones en el espacio se relacionan entre sí. La autocorrelación positiva sugiere que valores similares se agrupan en zonas cercanas, mientras que la negativa indica la alternancia de valores altos y bajos en el territorio.
Comprensión de la heterogeneidad espacial: Examinar cómo varían las relaciones y distribuciones de los datos a lo largo del espacio, lo que es esencial para el diseño de modelos que reflejen adecuadamente la complejidad de los procesos geográficos.
2.3.1 Técnicas y herramientas utilizadas
Tal como se ha comentado en el apartado Sección 2.2, la representación gráfica es uno de los primeros pasos en la exploración espacial. Los mapas temáticos permiten representar variables de forma intuitiva, mientras que los mapas de calor ayudan a visualizar la densidad o intensidad de eventos en el espacio, facilitando la identificación de zonas críticas o de alta concentración. Es importante tener en cuenta los principios básicos de la visualización espacial, así como las diferentes tipologías y herramientas disponibles para asegurar una representación precisa y útil de los datos.
2.3.1.1 Análisis de autocorrelación espacial
Indicadores como el Índice de Moran y la Estadística de Geary son herramientas fundamentales para cuantificar la autocorrelación. El Índice de Moran, por ejemplo, evalúa si la distribución de una variable es aleatoria o si existe una dependencia espacial, proporcionando una medida global del fenómeno. Complementariamente, el uso de Indicadores Locales de Autocorrelación Espacial (LISA) permite identificar áreas específicas que contribuyen significativamente a la autocorrelación global, destacando clusters o áreas atípicas. Cabe mencionar que las estadísticas espaciales se abordarán en futuras sesiones, lo que permitirá profundizar en la interpretación y aplicación de estos indicadores.
2.3.1.2 Análisis de vecinos y matriz de contigüidad
Establecer la definición de vecindad es clave para el análisis espacial. Las matrices de contigüidad (basadas en criterios como la contigüidad de borde o de vértice) o las distancias definidas permiten modelar las relaciones espaciales entre observaciones. Estas definiciones son esenciales para la aplicación de técnicas de autocorrelación y para la identificación de estructuras espaciales.
2.3.1.3 Técnicas de clustering espacial
Algoritmos de agrupamiento, como el DBSCAN (Density-Based Spatial Clustering of Applications with Noise) y otros métodos adaptados al contexto espacial, se utilizan para detectar agrupamientos naturales en los datos, considerando tanto la proximidad geográfica como las características intrínsecas de las variables analizadas.
2.3.2 Proceso de exploración
El proceso de exploración espacial generalmente se estructura en las siguientes etapas:
Pre-procesamiento y limpieza de datos: Se revisa la calidad y consistencia de los datos espaciales, corrigiendo errores, normalizando formatos y asegurando que las coordenadas y proyecciones sean correctas.
Visualización inicial: La representación gráfica de los datos a través de mapas y diagramas (ver Sección 2.2) facilita la identificación preliminar de patrones y anomalías. Esta etapa facilita la formulación de hipótesis y definir la dirección del análisis posterior.
Cálculo de estadísticas espaciales: Se aplican indicadores globales y locales de autocorrelación, así como medidas descriptivas específicas, para cuantificar y validar la existencia de patrones espaciales. Estas cuestiones se aboradrán en profundid en sesiones posteriores.
Interpretación y validación: Los resultados obtenidos se interpretan en el contexto del fenómeno estudiado, considerando posibles factores externos que pueden influir en la distribución espacial. Además, se validan mediante la comparación con estudios previos o el uso de datos complementarios.