3 Modelos espaciales

Los modelos espaciales constituyen una herramienta fundamental en el análisis y la interpretación de datos geográficos. Su objetivo principal es captar las relaciones espaciales, patrones de distribución y variabilidad que ocurren en el espacio, permitiendo describir, modelar y, en algunos casos, predecir fenómenos que tienen una dependencia explícita con su ubicación geográfica. Estos modelos surgen de la necesidad de abordar la complejidad inherente a los datos espaciales, que suelen estar influenciados por la proximidad, las interacciones locales y las características del entorno. En este tema, exploraremos tres enfoques principales que permiten analizar los datos espaciales desde distintas perspectivas: procesos puntuales, geoestadística y datos regionales.

3.1 Procesos puntuales

Como vimos en anteriormente, los datos espaciales se componen de dos elementos:

Las localizaciones \(\{s_1, ..., s_n\}\) sobre una superficie, generalmente La Tierra, y que habitualmente están formadas por duplas \((x_i, y_i)\) o Latitud y Longitud (coordenadas).
Los datos \(\{Z(s_1),...,Z(s_n)\}\) observados sobre esas localizaciones (el número de ventas por tienda o el número de pacientes que hay en un hospital, por ejemplo). En resumen, estos datos son el resultado de la observación de una variable \(Z\), unidimensional o multidimensional.

Según el tipo de localización \(s\) que se considere, los datos espaciales se denominan y analizan de forma diferente. Si las localizaciones \(\{s_1, ..., s_n\}\) son fijas hablamos de Geoestadística (apartado 3). Si las localizaciones son valores aislados y no son fijas sino que también son aleatorias (independientes de \(Z\)) se habla de Procesos Puntuales (Point Patterns). Un ejemplo podría ser los árboles en un bosque. Por último, cuando los datos están agrupados decimos que son Datos Regionales o lattice data (apartado 4).

3.1.1 Procesos Puntuales espaciales

Los Modelos Espaciales puntuales (Spatial Point Patterns) fueron utilizados inicialmente por botánicos y ecólogos en los años 30 del siglo XX para determinar, por ejemplo, la distribución espacial de los datos y sus causas en unas determinadas especies, o para comparar si podía admitirse que dos especies estaban igualmente distribuidas. En la actualidad estos modelos se implementan en una gran variedad de campos, como en la arqueología, la epidemiología, la astronomía, la criminología, la analítica de negocios…

Por ejemplo, es posible diseñar un modelo para comprender mejor la ubicación de los delitos, o estudiar si los casos de una cierta enfermedad están distribuidos geográficamente siguiendo un determinado modelo. En todos los casos, los datos observados serán del tipo \((x_i, y_i)\) y, si se quieren comparar poblaciones, tendrán asociados una marca (género, edad…) que identifique las poblaciones a comparar.

Los tres propósitos para los que se usan los Procesos Puntuales Espaciales son:

Analizar la distribución que presentan los datos espaciales para concluir:
- si están distribuidos aleatoriamente, es decir, al azar y sin ningún modelo que rija las localizaciones observadas;
- si están distribuidos regularmente, es decir, están uniformemente espaciados;
- si están distribuidos formando clusters.
Analizar la densidad espacial, es decir, el número de individuos por unidad de área.
Analizar las marcas para, por ejemplo, comparar el comportamiento de dos especies.

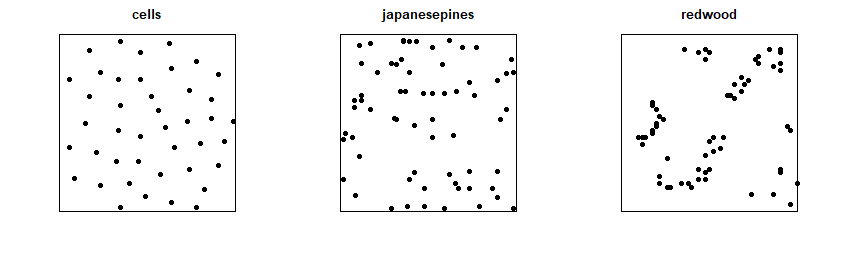
A continuación se muestran tres ejemplos (hablaremos de ello en la sesión práctica) en los que se representan ciertas ubicaciones en regiones muestrales cuadradas:

library(spatstat)
par(mfrow = c(1,3))
plot(cells)
plot(japanesepines)
plot(redwood)

3.1.2 Análisis de distribución espacial

Antes de abordar los tres objetivos anteriores es necesario recordar algunos conceptos matemáticos y estadísticos.

Un Proceso Estocástico es una sucesión de observaciones de origen aleatorio. Cuando decimos sucesión nos estamos refiriendo a que las observaciones se obtienen siguiendo un orden que puede ser temporal (como ocurre con las Series Temporales) o espacial (el que aquí nos ocupa) o, incluso, espaciotemporal (lo veremos más adelante). Formalmente, un Proceso Estocástico es una sucesión de variables aleatorias \(X_t\) que evolucionan en función de otra variable (la que marca el orden) denominada índice \(t\) (el tiempo o el espacio). Cada una de las variables aleatorias del proceso tiene su propia distribución de probabilidad y, entre ellas, pueden estar correlacionadas o no.

Un Proceso Puntual Espacial es un proceso estocástico que genera localizaciones de algunos sucesos de interés dentro de una región concreta objeto de estudio.

Denominaremos Modelo Espacial Puntual a las localizaciones de los sucesos generados por un proceso puntual en el área objeto de estudio. Si las localizaciones tienen marcas para distinguir varios grupos de datos, hablaremos de Proceso y Modelo Espacial Puntual con Marcas.

3.1.3 Aleatoriedad Espacial Completa

El primer objetivo del Análisis de la distribución de las localizaciones es averiguar si éstas están distribuidas al azar en la región objeto de estudio. En ocasiones la aleatoriedad puede intuirse, es decir, podemos observar que no existe ningún patrón que regule la ubicación de los puntos. Esta idea se denomina Aleatoriedad Espacial Completa (Complete Spatial Randomness) o CSR y se formaliza matemáticamente con un Proceso de Poisson homogéneo de parámetro \(\lambda\), ya que este tipo de procesos se caracteriza por tres propiedades:

El número de localizaciones en una región \(A\) de área \(|A|\) sigue una distribución de Poisson con media \(\lambda|A|\), en donde \(\lambda\) es la intensidad del proceso, es decir, el número esperado de localizaciones por unidad de área.
Dadas \(n\) localizaciones en una región \(A\), es decir, condicionalmente a que hay \(n\) localizaciones en \(A\), éstas se distribuyen según una distribución uniforme sobre \(A\).
En dos regiones disjuntas \(A\) y \(B\), el número de localizaciones en \(A\) y el número de localizaciones en \(B\) son variables aleatorias independientes.

Para analizar si los datos siguen o no CSR, es decir, un proceso de Poisson homogéneo, podemos anotar el número de localizaciones acaecidas en cuadrados (Quadrant Test) en los que se ha dividido la zona de estudio y comparar mediante un test \(\chi^2\) de bondad del ajuste si se cumple ese modelo Poisson, pero este método es poco preciso, por lo que es más frecuente utilizar métodos basados en distancias.

3.1.4 Distancia a la localización más cercana

Hay varias posibilidades de distancia aunque suele utilizarse la distancia (Euclídea) entre una localización y la localización vecina más cercana (nearest-neighboring). Se puede demostrar que si las localizaciones están generadas por un proceso de Poisson homogéneo de parámetro \(\lambda\), es decir, al azar, la distribución de estas distancias viene dada por la siguiente función de densidad: \[g(w) = 2 \pi \lambda w e^{-\pi \lambda w^2} \phantom{aaaaa} w > 0\]

o equivalentemente, por la siguiente función de distribución: \[G(w) = 1 - e^{-\pi \lambda w^2} \phantom{aaaaa} w > 0\]

Por tanto, las localizaciones observadas estarán generadas al azar, es decir, no siguiendo ningún patrón, si las diferencias entre su función de distribución empírica y este modelo teórico \(G\) no son significativas.

Existen varios test de hipótesis para contrastar la aleatoriedad CSR, como los citados en Cressie (1993) o los comentados en Diggle (2003).

3.1.5 Ajuste de Modelos Espaciales Puntuales

Si hemos rechazado la CSR (Aleatoriedad Espacial Completa) de una región \(A\), es decir, que las localizaciones observadas en \(A\) no se producen al azar, el siguiente paso lógico es ajustar un modelo a las localizaciones observadas. Si rechazamos la CSR tenemos dos posibilidades: la distribución regular y la formación de clusters.

Una distribución regular o uniforme implica, como hemos adelantado anteriormente, que las localizaciones están uniformemente espaciadas. Este fenómeno se suele modelizar mediante Procesos de Inhibición Simple.

La segunda posibilidad es que se produjeran clusters, es decir, agrupamientos de localizaciones. Esta segunda posibilidad se puede modelizar mediante un Proceso de Poisson no homogéneo (la CSR lo era mediante un Proceso de Poisson homogéneo), mediante un Proceso de Cox o mediante un Proceso de Poisson con clusters. Nosotros sólo analizaremos el Proceso de Poisson no homogéneo de parámetro \(\lambda(s)\), que se diferencia del homogéneo comentado anteriormente porque la intensidad del proceso \(\lambda(s)\) ya no es constante, sino que depende de la localización \(s \in A\).

3.1.6 Estimación de la Intensidad

En un proceso de Poisson homogéneo la intensidad es constante en cada área considerada \(A\), por lo que, si en ese área hay \(n\) localizaciones, un estimador suyo será \(\hat{\lambda}=\frac{n}{|A|}\) en donde \(|A|\) representa el área de la región \(A\).

En el caso de procesos de Poisson no homogéneos hay varias posibilidades que se resumen en dos: utilizar Métodos Paramétricos, consistentes en proponer una función cuyos parámetros son estimados por el método de máxima verosimilitud. Esta vía permite incluir \(p\) covariables existentes \(Z_j, \;j = 1, ..., p\) y utilizar, por ejemplo, un modelo log-lineal de la forma \[log\lambda(s)=\sum_{j=1}^{p}\beta_jZ_j(s)\]

siendo \(Z_j(s) \; j=1,...,p\) los valores que toman las covariables en la localización \(s\).

La segunda posibilidad en la estimación de un proceso de Poisson no homogéneo son los Métodos no Paramétricos, basados en el Estimador Núcleo Suavizado (kernel smoothing) dado por \[\hat{\lambda}(s)=\frac{1}{q(||s||)h^2}\sum_{i=1}^{n}K \left( \frac{||s-s_i||}{h} \right)\]

suponiendo que se han observado \(n\) localizaciones \(s_1,...,s_n\), siendo \(K\) la función núcleo considerada (habitualmente bivariante), \(q_s\) una corrección frontera para compensar los valores que se pierden cuando \(s\) está cerca de la frontera de la región \(A\), y siendo \(h\) una medida del nivel de suavizado (smoothing), también denominada ancho de banda (bandwith), que se quiere considerar: valores pequeños de \(h\) conducirán a estimadores poco suaves y valors grandes a estimadores muy suaves.

La función núcleo habitualmente considerada es la denominada función cuártica (quartic), también denominada biponderada (biweigth) definida, para localizaciones \(s \in (-1, 1)\), como \(K(s)=\frac{3}{\pi}(1-||s||)^2\) y como \(0\) para localizaciones \(s \notin (-1,1)\).

Nota: \(||s||\) denota la norma o longitud del vector \(s\), que si es bidimensional tiene coordenadas \((s_1, s_2)\), y es igual a \(||s||=\sqrt{s_1^2 + s_2^2}\)

3.1.7 Análisis de la densidad espacial

El objetivo de determinar el número de individuos por unidad de área se consigue fácilmente con la función summary.

library(spatstat)
summary(cells)

Planar point pattern:  42 points
Average intensity 42 points per square unit

Coordinates are given to 3 decimal places
i.e. rounded to the nearest multiple of 0.001 units

Window: rectangle = [0, 1] x [0, 1] units
Window area = 1 square unit

summary(japanesepines)

Planar point pattern:  65 points
Average intensity 65 points per square unit (one unit = 5.7 metres)

Coordinates are given to 2 decimal places
i.e. rounded to the nearest multiple of 0.01 units 
(one unit = 5.7 metres)

Window: rectangle = [0, 1] x [0, 1] units
Window area = 1 square unit
Unit of length: 5.7 metres

summary(redwood)

Planar point pattern:  62 points
Average intensity 62 points per square unit

Coordinates are given to 3 decimal places
i.e. rounded to the nearest multiple of 0.001 units

Window: rectangle = [0, 1] x [-1, 0] units
                    (1 x 1 units)
Window area = 1 square unit

3.1.8 Análisis de marcas

Como hemos hecho en varias ocasiones, podemos analizar nuestros datos de forma agregada (centros educativos) o diferenciando según una determinada variable: por régimen (público, privado y concertado), por niveles formativos impartidos (primaria, secundaria, formación profesional, personas adultas…), etc.

3.2 Geoestadística

3.2.1 Introducción

Cuando hablamos de Geoestadística generalmente nos referimos al análisis de datos espaciales \({Z(s_1), ...,Z(s_n)}\) en donde las localizaciones \({s_1, ..., s_n}\) no son aleatorias (procesos puntuales), sino fijas (variables de tipo continuo: elevación, temperatura, calidad del aire…).

Es muy habitual que no tengamos observaciones de \(Z\) en todas las localizaciones deseadas, siendo uno de los propósitos de la Geoestadística hacer predicciones (generalmente mediante interpolaciones) de \(Z\) en algunas localizaciones \(s_0\) en donde se desconoce su valor. También suele ser de interés conocer la media de \(Z\) en alguna zona determinada, \(B_0\).

Estos dos objetivos se suelen conseguir estimando y modelizando la correlación espacial (covarianza o semivarianza) y analizando la estacionariedad, tanto en localizaciones concretas como en redes, mallas o grids.

3.2.2 Variograma

Los variogramas, elementos clave para definir la autocorrelación espacial, se fundamentan en el concepto de semivarianza.

La semivarianza es una medida de autocorrelación espacial de una variable \(x\) entre dos puntos \(i,j\), y viene expresada por:

\[ \gamma(s)=\frac{1}{2}(z_i-z_j)^2 \]

Puesto que puede calcularse la distancia entre dichos puntos, pueden representarse los valores de \(\gamma\) frente a las distancias \(h\), obteniendo una nube de puntos (nube del variograma) como esta:

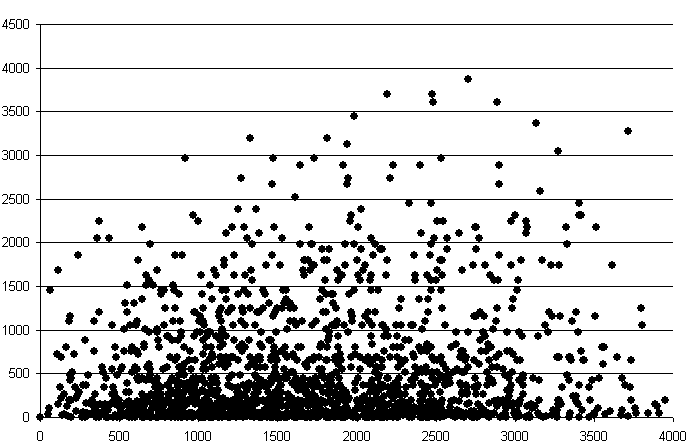
Esta nube aporta, en principio, poca información, pero puede resumirse agrupando los pares de puntos por intervalos de distancia, y calculando la media de todas las semivarianzas en cada intervalo. De esta forma se tiene una función que relaciona la semivarianza con la distancia entre los puntos, según

\[ \gamma(h)=\frac{1}{2m(h)}\sum_{i=1}^{m(h)}(x_i-x_j)^2 \] siendo \(m(h)\) el número de puntos del conjunto separados entre sí por una distancia \(h\).

En la práctica se establecen una serie de valores de distancia equiespaciados, cada uno de los cuales define un intervalo centrado en dicho valor. La función \(m(h)\) representa el número de puntos en cada bloque. Es importante que este número de puntos en cada bloque sea significativo, especialmente para dar validez al posterior ajuste sobre estos valores medios, como más adelante veremos. La función \(\gamma(h)\) es lo que se conoce como variograma experimental o semivariograma.

La elección de un tamaño óptimo para los intervalos es importante para obtener un variograma fiable. Si en el variograma aparecen ondulaciones, esto puede ser señal de que existe un comportamiento cíclico de la variable, pero más probablemente de que la distancia del intervalo no ha sido bien escogida.

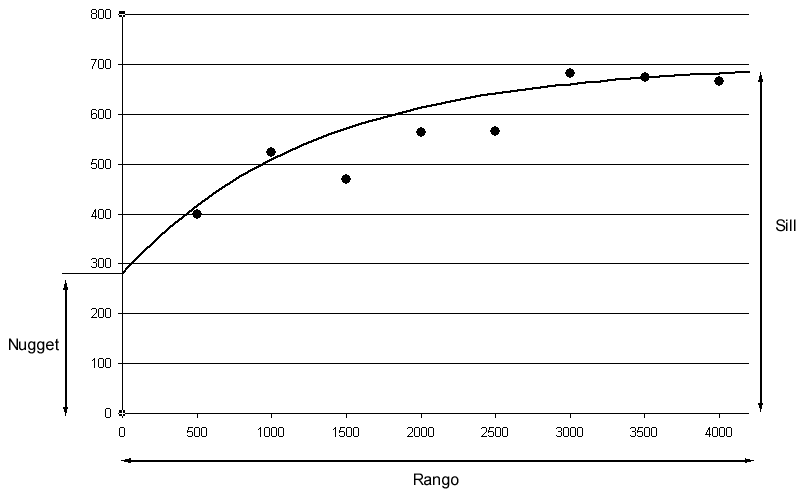
Como puede verse en la figura anterior, la curva que los puntos del variograma experimental describen da lugar a la definición de unos elementos básicos que lo caracterizan:

Rango: representa la máxima distancia a partir de la cual existe dependencia espacial. Es el valor en el que se alcanza la máxima varianza, o a partir del cual ya presenta una tendencia asintótica.
Sill: representa la máxima variabilidad en ausencia de dependencia espacial.
Nugget: conforme la distancia tiende a cero, el valor de la semivarianza tiende a este valor. Representa aquella variabilidad que no puede explicarse mediante la estructura espacial.

A partir de los puntos que forman el variograma experimental, puede definirse un modelo que aporta información sobre el proceso subyacente, a partir de su forma y sus parámetros. La definición de este modelo implica el ajuste de una curva a los puntos del variograma experimental, y tiene como resultado la obtención de un variograma teórico.

Existen muchas alternativas para elegir una función para el variograma teórico. Aquí se muestran algunos:

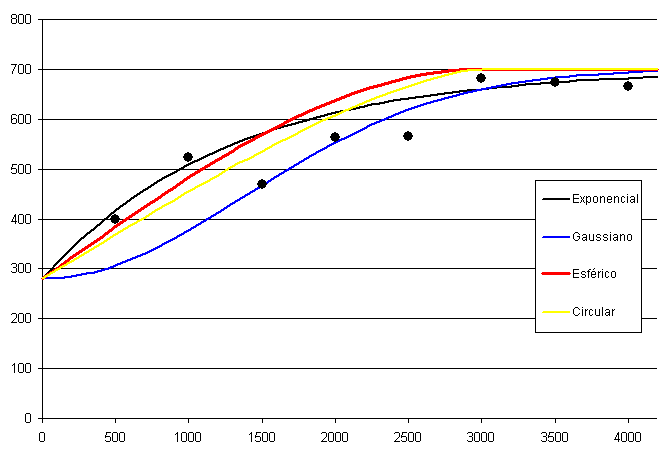
3.2.3 Interpolación espacial

Un método de interpolación permite el calculo de valores en puntos no muestreados, a partir de los valores recogidos en otra serie de puntos. Veamos este concepto mediante un sencillo ejemplo:

Los cuatro puntos señalados en la figura han sido muestreados y se dispone de un valor para cada uno de ellos. Como se puede observar, los puntos no han de encontrarse necesariamente en el centro de las celdas. Queremos estimar los valores en las celdas de la malla, en particular en la celda marcada con un interrogante.

La lógica nos indica que el valor en esta celda debe estar alrededor de 10, ya que este valor sigue la tendencia natural de los valores recogidos, que tiene todos ellos un valor de esa magnitud. Si aplicamos cualquiera de los métodos de interpolación que veremos a continuación, el valor que obtengamos será con seguridad muy aproximado a esa cifra.

Otro ejemplo sería el siguiente:

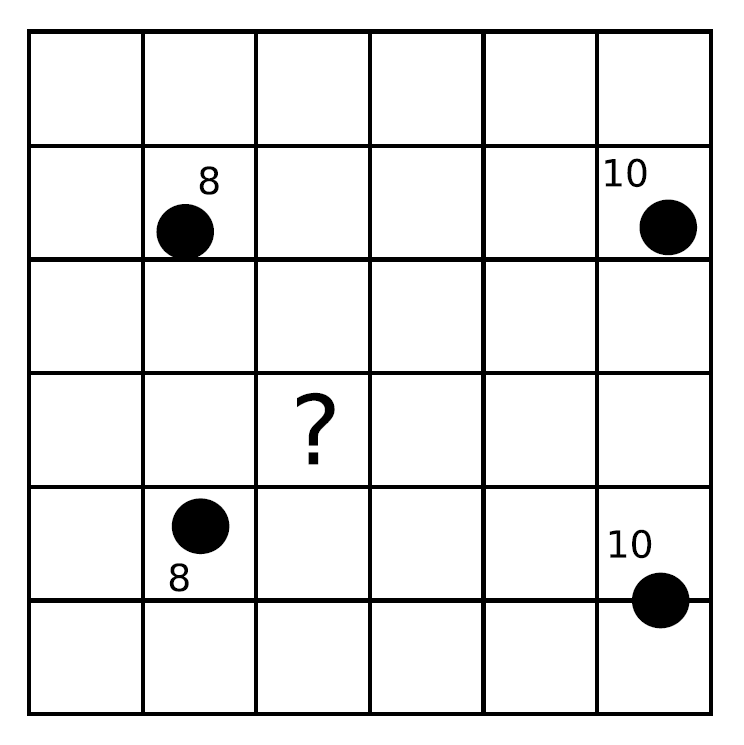
En este caso, la lógica nos indica que el valorá ser inferior a 10, y también probablemente a la media de los valores muestrales (9), ya que la celda en cuestión se sitúa más cerca de los valores inferiores que de los superiores a ese valor medio. Razonando de este modo, aplicamos el hecho de que la proximidad incrementa la semejanza de valores. Es decir, que existe autocorrelación espacial para la variable interpolada.

El caso siguiente ya es algo distinto:

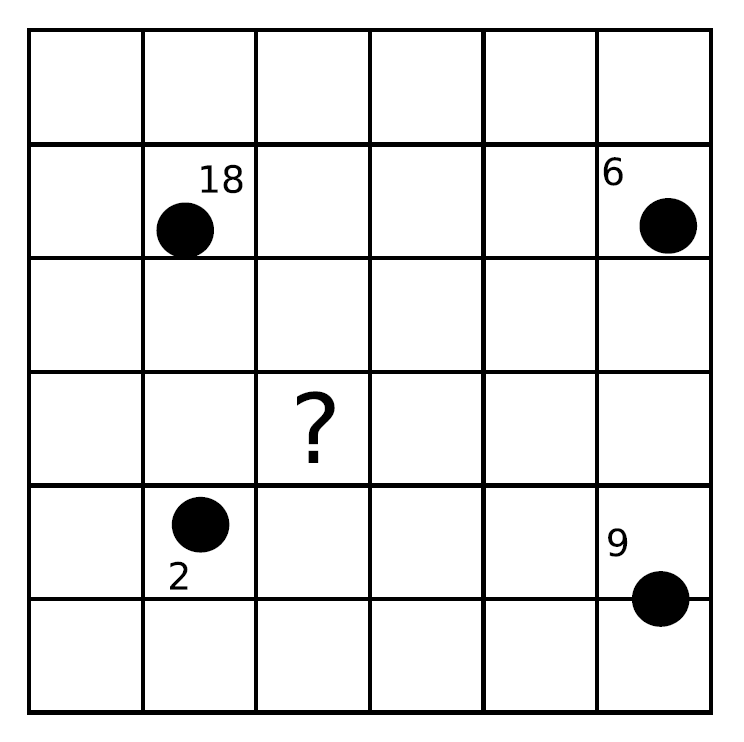
En este caso, no parece tan sencillo “adivinar” el valor que corresponde. Esto es así no porque las operaciones sean más complejas, sino porque no existe de la misma forma que en los ejemplos anteriores la autocorrelación espacial de la variable, y esa lógica no resulta tan obvia. Utilizando los distintos métodos de interpolación, puede ser que estos den valores distintos, ya que se comportarán de forma diferente ante tal situación.

A pesar de las diferencias que puedan existir entre los diferentes métodos de interpolación, todos persiguen el mismo objetivo: replicar de la forma más precisa posible un campo a partir de un conjunto definido de puntos con valores de este.

3.2.4 Métodos de Interpolación

Existen muchos métodos de interpolación, de los cuales algunos cuentan con más presencia en los SIG por estar más adaptados al tipo de dato que se maneja. Podemos clasificar los distintos métodos de interpolación según varios criterios:

Según los puntos considerados para el cálculo de valores. Algunos métodos consideran que todos los puntos de los que disponemos tienen influencia sobre el valor a calcular en una celda. Estos modelos se conocen como globales. En otros, denominados locales, solo se considera un conjunto restringido de estos. Este conjunto puede establecerse por medio de un umbral de distancia (todos los situados a una distancia menor que el umbral), de conteo (los \(n\) puntos más cercanos), o bien ambos.
Según su valor en los puntos de partida. En algunos métodos, denominados exactos, los valores asignados a las coordenadas correspondientes a los puntos de origen son exactamente los recogidos en dichos puntos. En los métodos aproximados, el valor en esas celdas es el que corresponde al mejor ajuste, y no ha de coincidir necesariamente con el valor original.
Según la inclusión o no de elementos probabilísticos. Diferenciamos entre métodos estocásticos (aquellos que emplean elementos probabilísticos) y métodos determinísticos (aquellos que no los emplean).

3.2.4.1 Interpolación por vecindad

El método más sencillo de interpolación es el de vecindad o vecino más cercano. En él se asigna directamente a cada celda el valor del punto más cercano. No existe formulación matemática que emplee las distancias entre puntos o los valores de estos, sino que el valor resultante es sencillamente el del punto más próximo.

Se trata, por tanto, de un método local, exacto y determinístico. El resultado es una capa con saltos abruptos, como se puede ver a continuación:

La interpolación por vecindad no es adecuada para el trabajo con variables continuas, pero sí para variables categóricas.

3.2.4.2 Métodos basados en ponderación por distancia

Los métodos basados en ponderación por distancia son algoritmos de interpolación de tipo local, aproximados y determinísticos. El valor en una coordenada dada se calcula mediante una media ponderada de los puntos de influencia seleccionados (bien sea la selección por distancia o por número de estos). Su expresión es de la forma

\[ \begin{equation} \hat{z}=\frac{\sum_{i=1}^{n}{p_i}{z_i^k}}{\sum_{i=1}^{n}{p_i^k}} \end{equation} \]

siendo \(p_i\) el peso asignado al punto \(i\)–ésimo. Este peso puede ser cualquier función dependiente de la distancia. La función más habitual es la que da lugar al método de ponderación por distancia inversa (Inverse Distance Weighted Interpolation) o IDW, de la forma

\[ p_i=\frac{1}{d_i^k} \]

donde el exponente \(k\) toma habitualmente los valores 1 o 2. Este parámetro permite controlar la significancia de puntos conocidos en los valores interpolados basándose en la distancia desde el punto de salida, es decir, a mayor \(k\), más alto será el peso que tengan las muestras más cercanas.

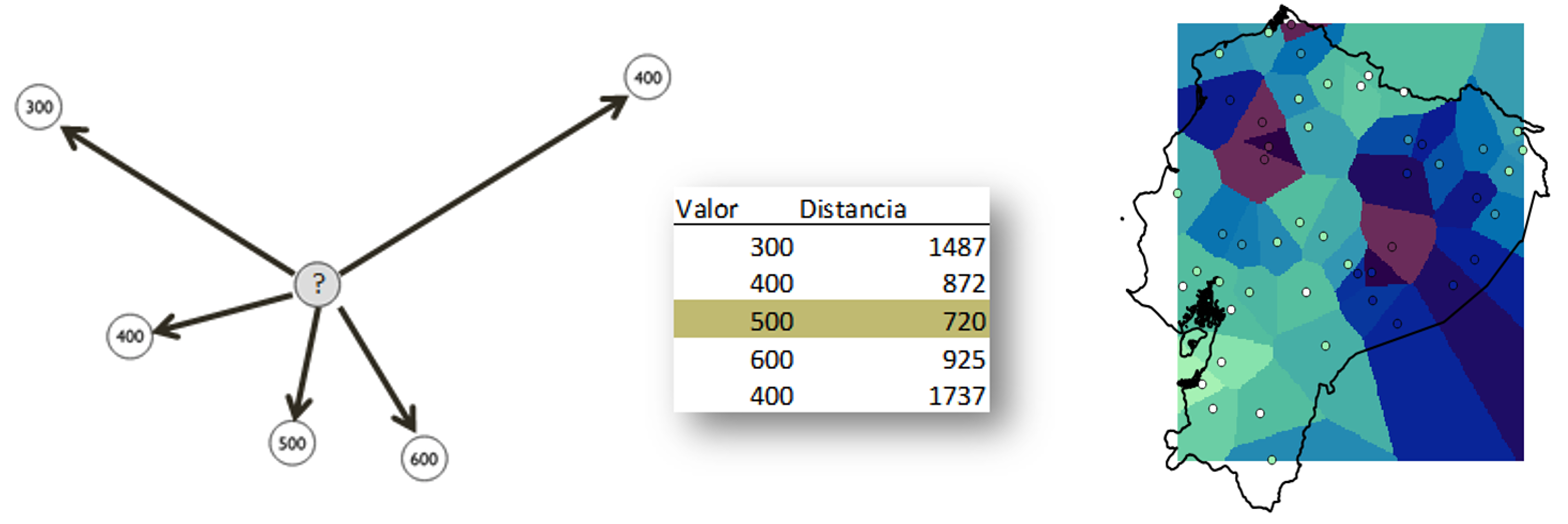
Así, dado

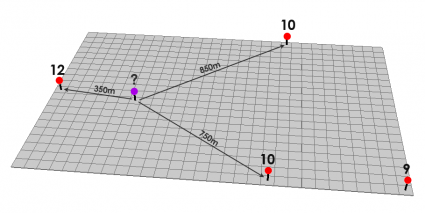
si \(k=1\), tenemos que

\[ \frac{12/350+10/750+10/850}{1/350+1/750+1/850}=11.1 \]

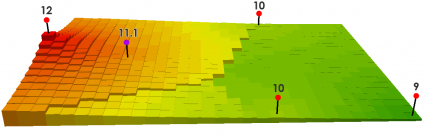
y si \(k=2\), tenemos que

\[ \frac{(12/350)^2+(10/750)^2+(10/850)^2}{(1/350)^2+(1/750)^2+(1/850)^2}=11.4 \]

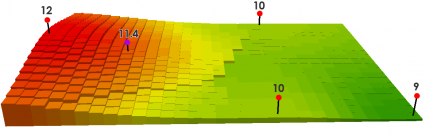
Los métodos basados en ponderación por distancia solo tienen en cuenta el alejamiento, pero no la posición. Es decir, un punto situado a una distancia \(d\) hacia el Norte tiene la misma influencia que uno situado a esa misma distancia \(d\) pero hacia el Oeste.

Igualmente, los métodos basados en distancia no generan valores que se encuentren fuera del rango de valores de los datos de entrada. Eso causa efectos indeseados en caso de que el muestreo de datos no recoja los puntos característicos de la superficie interpolada.

3.2.4.3 Ajuste de funciones. Superficies de tendencia

El ajuste de funciones es un método de interpolación determinístico o estocástico (según el tipo de función a ajustar), aproximado y global. Puede aplicarse de forma local, aunque esto resulta menos habitual. Dado el conjunto completo de los puntos de partida, se estima una superficie definida por una función de la forma

\[ \hat{z}=f(x,y) \]

El ajuste de la función se realiza por mínimos cuadrados. Estas funciones son de tipo polinómico, y permiten el cálculo de parámetros en todas las celdas de la capa ráster. Por su propia construcción, requieren pocas operaciones y son rápidos de calcular. Sin embargo, esta sencillez es también su principal inconveniente.

Los polinomios de grado cero (plano constante), uno (plano inclinado), dos (colina o depresión) o tres, son todos ellos demasiado simples, y las variables continuas que pueden requerir un proceso de interpolación dentro de un SIG son por lo general mucho más complejas. El empleo de funciones de ajuste permite incorporar otras variables adicionales \(h_i\) mediante funciones de la forma

\[ \hat{z}=f(x,y,h_1,...,h_n) \]

Esto posibilita la incorporación de variables de apoyo (predictores) que pueden tener una influencia en la variable interpolada, considerando así no únicamente la posición de los distintos puntos, sino los valores en ellos de dichas variables de apoyo.

3.2.4.4 Curvas adaptativas o splines

Las curvas adaptativas o splines conforman una familia de métodos de interpolación exactos, determinísticos y locales. Desde un punto de vista físico pueden asemejarse a situar una superficie elástica sobre el área a interpolar, fijando esta sobre los puntos conocidos. Crean así superficies suaves, cuyas características pueden regularse modificando el tipo de curva empleada o los parámetros de esta, de la misma forma que sucedería si se variasen las cualidades de esa membrana ficticia.

La superficie creada cumple la condición de minimizar con carácter global alguna propiedad tal como la curvatura. Desde un punto de vista matemático, los splines son funciones polinómicas por tramos, de tal modo que en lugar de emplear un único polinomio para ajustar a todo un intervalo, se emplea uno distinto de ellos para cada tramo.

Los splines no sufren los principales defectos de los métodos anteriores. Por un lado, pueden alcanzar valores fuera del rango definido por los puntos de partida. Por otro, el mal comportamiento de las funciones polinómicas entre puntos se evita incluso al utilizar polinomios de grados elevados. No obstante, en zonas con cambios bruscos de valores (como por ejemplo, dos puntos de entrada cercanos pero con valores muy diferentes), pueden presentarse oscilaciones artificiales significativas.

3.2.4.5 Interpolación kriging

El kriging es un método de interpolación estocástico, exacto, aplicable tanto de forma global como local. Se trata de un método complejo con una fuerte carga (geo)estadística, del que existen además diversas variantes.

El kriging se basa en la teoría de variables regionalizadas. El objetivo del método es ofrecer una forma objetiva de establecer la ponderación óptima entre los puntos en un interpolador local. Tal interpolación óptima debe cumplir los siguientes requisitos, que son cubiertos por el kriging:

El error de predicción debe ser mínimo.
Los puntos cercanos deben tener pesos mayores que los lejanos.
La presencia de un punto cercano en una dirección dada debe restar influencia (enmascarar) a puntos en la misma dirección pero más lejanos.
Puntos muy cercanos con valores muy similares deben “agruparse”, de tal forma que no aparezca sesgo por sobremuestreo.
La estimación del error debe hacerse en función de la estructura de los puntos, no de los valores.

Pregunta

¿Cuál es el origen del método kriging?

Junto con la superficie interpolada, el kriging genera asimismo superficies con medidas del error de interpolación, que pueden emplearse para conocer la bondad de esta en las distintas zonas (importante novedad respecto de los métodos expuestos anteriormente).

En su expresión fundamental, el kriging es semejante a un método basado en ponderación por distancia. Dicha expresión es de la forma

\[ \hat{z}=\sum_{i=1}^{n}z_i\Lambda_i \] siendo \(\Lambda_i\) los pesos asignados a cada uno de los puntos considerados. El cálculo de estos pesos, no obstante, se realiza de forma más compleja que en la ponderación por distancia, ya que en lugar de utilizar dichas distancias se acude al análisis de la autocorrelación a través del variograma teórico. Por ello se requiere, asimismo, que exista un número suficiente de puntos (mayor de 50) para estimar correctamente el variograma.

A partir de los valores del variograma, se estima un vector de pesos que, multiplicado por el vector de valores de los puntos de influencia, da el valor estimado.

Como hemos adelantado anteriormente, existen diversas variantes del método kriging.

En el denominado kriging ordinario, e interpolando para un punto \(p\) empleando \(n\) puntos de influencia alrededor de este, el antedicho vector de pesos se calcula según

\[ \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \\ \lambda \end{pmatrix} = \begin{pmatrix} \gamma(d_{11}) & \dots & \gamma(d_{1n}) & 1 \\ \gamma(d_{21}) & \dots & \gamma(d_{2n}) & 1 \\ \vdots & \ddots & \vdots & 1 \\ \gamma(d_{n1}) & \dots & \gamma(d_{nn}) & 1 \\ 1 & \dots & 1 & 0 \end{pmatrix} \begin{pmatrix} \gamma(d_{1p}) \\ \gamma(d_{2p}) \\ \vdots \\ \gamma(d_{np}) \\ 1 \end{pmatrix} \]

La aplicación del kriging ordinario implica la asunción de una serie de características de los datos:

Estacionaridad de primer y segundo orden, es decir, la media y la varianza son constantes a lo largo del área interpolada, y la covarianza depende únicamente de la distancia entre puntos.
Normalidad de la variable interpolada.
Existencia de una autocorrelación significativa.

Cuando no puede asumirse la estacionariedad de primer orden y existe una tendencia marcada en el valor medio esperado en los distintos puntos, puede aplicarse un tipo de kriging denominado kriging universal. Además de los valores a interpolar y sus coordenadas, este método permite el uso de predictores relacionados con dicha tendencia.

El kriging con regresión es similar en cuanto a sus resultados e ideas, aunque la forma de proceder es distinta. Mientras que en el universal se trabaja con los residuos y la superficie de tendencia conjuntamente, este separa ambas partes y las analiza por separado, combinándolas después para estimar los valores y los errores asociados.

Existen muchas otras variaciones del kriging tales como el kriging simple, el kriging por bloques o el co–kriging. La aplicación de los mismos, no obstante, es restringida debido a que no es tan frecuente su implementación. Los SIG habituales implementan por regla general las variantes básicas anteriores, quedando las restantes para programas mucho más especializados.

3.2.4.6 Elección del método adecuado

Junto a los métodos de interpolación que hemos visto, que son los más comunes y los implementados habitualmente, existen otros muchos que aparecen en determinados SIG (vecino natural, interpolación picnofiláctica…). Además de esto, cada uno de dichos métodos presenta a su vez diversas variantes, con lo cual el conjunto global de metodologías es realmente extenso. A partir de un juego de datos distribuidos irregularmente, la creación de una malla ráster regular es, por tanto, una tarea compleja que requiere para empezar la elección de un método concreto. Este proceso de elección no es en absoluto sencillo.

No existe un método universalmente establecido como más adecuado en todas situaciones, y la elección se ha de fundamentar en diversos factores. Al mismo tiempo, un método puede ofrecer resultados muy distintos en función de los parámetros de ajuste, con lo que no solo se ha de elegir el método adecuado, sino también la forma de usarlo. Entre los factores a tener en cuenta para llevar esto a cabo, merecen mencionarse los siguientes:

Las características de la variable a interpolar.
La calidad de los datos de partida (cuando los datos de partida son de gran precisión, los métodos exactos pueden tener más interés, de cara a preservar la información original).
El rendimiento de los algoritmos (tiempo de procesado).
El conocimiento de los métodos (elevado número de ajustes y alta sensibilidad del método).

3.3 Datos Regionales

3.3.1 Introducción

En ocasiones los datos espaciales observados son áreas o zonas, lo que comúnmente se denomina datos agregados o regionales. A diferencia de los dos apartados anteriores, en los que analizábamos la relación entre ubicaciones/localizaciones (puntos) concretas (ligadas a valores discretos o continuos), en este caso las unidades de investigación, es decir, los datos observados, son polígonos, los cuales deben de tener los límites bien definidos. No obstante, por su propia definición, varias áreas (polígonos) pueden unirse y formar una nueva zona, por lo que es de gran interés analizar si existe autocorrelación espacial entre varias unidades ya que, en muchas ocasiones, lo que pasa en una zona está relacionado con lo que pasa en la zona adyacente.

3.3.2 Entornos y pesos de Áreas

Si queremos realizar un análisis de datos espaciales cuando estos son áreas, es necesario asignar pesos a las zonas objeto de estudio, fundamentalmente para conseguir residuos totalmente independientes (sin autocorrelación espacial), cosa que será necesaria cuando hagamos el ajuste de un modelo a este tipo de datos.

La determinación de las zonas (o clusters) a considerar ya es un problema en sí mismo. Por ello, supondremos que las zonas están ya definidas (CCAA, provincia, municipio, distrito, barrio, sección censal…). A la hora de fijar pesos a esas zonas, podemos asignar un peso igual a 1 a las zonas limítrofes y un peso igual a 0 a las zonas no limítrofes. Es decir, si una zona A tiene sólo una zona como vecina, el peso de A será 1; si A tiene dos zonas vecinas, su peso será 2. Esta forma de fijar pesos se denomina binaria y con ella, si una zona tiene a su alrededor 2 zonas, su peso será el doble que el de otra zona con sólo una zona limítrofe.

La forma natural de contar cuántos vecinos tiene una zona es unir los centroides de las zonas. El número de conexiones entre los centroides nos dará su peso. Esta forma de asignar pesos hará que algunas áreas tengan peso 2 y otras peso 7, por ejemplo. Otra forma de asignar pesos se denomina ponderada, en donde los pesos de cada área son estandarizados de forma que todos los pesos sumen 1.

Por ejemplo, para el caso de las provincias españolas situadas en la Península Ibérica:

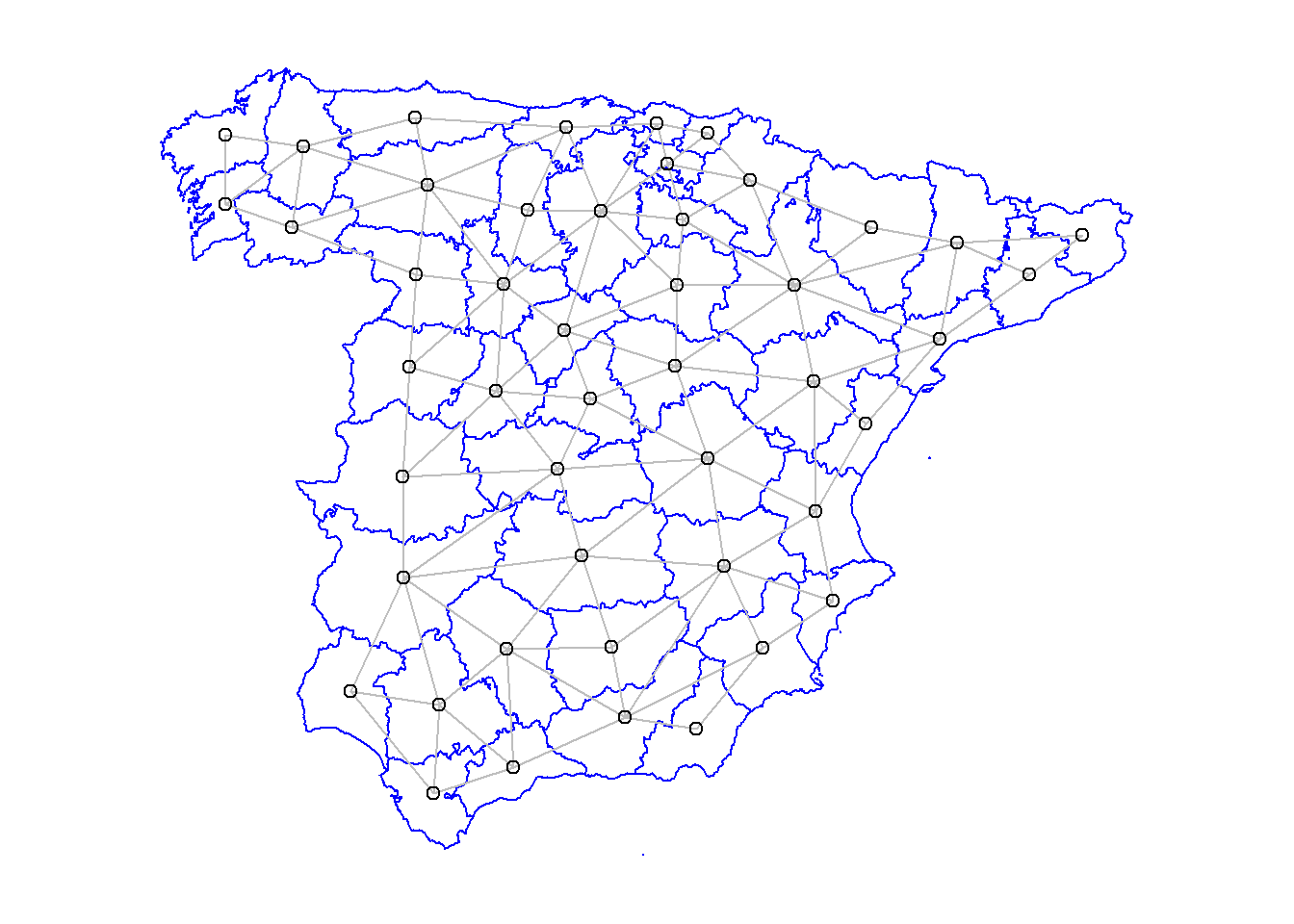
La función nb2mat() de la librería spdep es la que calcula los pesos de las zonas de las dos maneras antes mencionadas, las cuales se indican con el argumento style, asignando el valor "B" cuando lo hace de forma binaria, "W" en el caso de la forma ponderada (por filas) y "C" para ponderar globalmente. Hay una cuarta opción ("S"), siguiendo el método propuesto por Tiefelsdorf y Boots (1999).

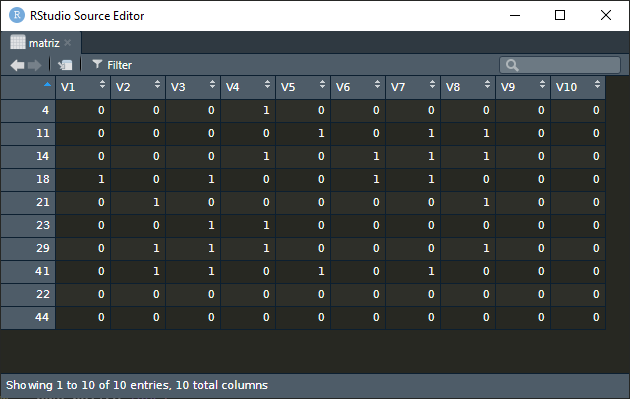
3.3.3 Contraste global de autocorrelación espacial

El estadístico (índice) I de Moran se utiliza para detectar la presencia de correlación espacial en observaciones tomadas en una malla o grid, siguiendo la siguiente expresión:

\[ \begin{equation} I=\frac{n}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}} \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij} (y_i-\overline{y}) (y_j-\overline{y})}{\sum_{i=1}^n (y_i-\overline{y})^2} \end{equation} \] Representamos con \(w_{ij}\) el peso espacial de la unión entre el individuo \(i\)-ésimo de la matriz de datos (fila \(i\)-ésima) y el individuo \(j\)-ésimo en donde se habrá medido la variable de interés, obteniendo respectivamente los valores \(y_i\) e \(y_j\). Es decir, con \(y_i\) lo que representamos es el valor de \(Z\) en \(s_i\), o lo que es lo mismo, \(Z(s_i)\).

Este índice toma un valor comprendido entre −1 y 1. Si es \(I = 0\) interpretamos que los datos están distribuidos al azar (algo similar al CSR que vimos en procesos puntuales). Si es positivo significa que hay concentración y, si toma un valor negativo, entendemos que hay una dispersión mayor de la que tendríamos si los datos se distribuyeran al azar.

El valor esperado del índice \(I\), bajo la hipótesis nula de ausencia de autocorrelación espacial, es \(E[I] = −1/(n − 1)\). Habitualmente se calculan los valores de este índice, de su media, de su varianza, de la desviación estándar, así como del p-value del test de la hipótesis nula de ausencia de autocorrelación espacial.

El test de Moran comentado en el punto anterior es un test global de autocorrelación espacial. El valor obtenido con ese test global se puede dividir para conseguir test locales que permitan detectar clusters en donde las observaciones sean similares a las de su entorno, así como detectar outliers locales, también denominados puntos calientes o hotspots.

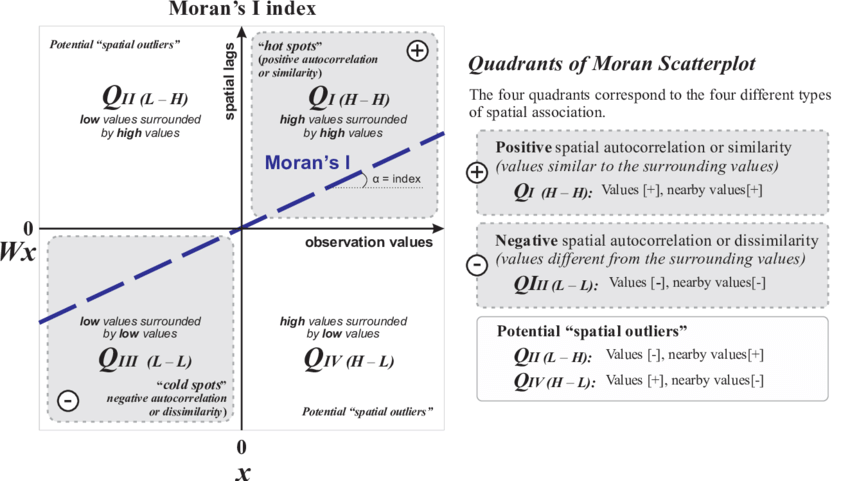
Comencemos estudiando el Gráfico de dispersión de Moran. Este gráfico (scatterplot) es un gráfico de dispersióon en donde aparecen en el eje de abscisas (eje X) los valores de la variable de interés y en el eje de ordenadas (eje Y) esos mismos valores retardados espacialmente (promedio ponderado de la variable de interés). Este gráfico está dividido en 4 cuadrantes, recogiendo los siguientes pares de valores:

High-High (Alto en X, Alto en Y): valores superiores a la media (puntos calientes).
High-Low (Alto en X, Bajo en Y): resultados atípicos con valores superiores/inferiores a la media.
Low-Low (Bajo en X, Bajo en Y): valores inferiores a la media o puntos fríos.
Low-High (Bajo en X, Alto en Y): resultados atípicoscon valores inferiores/superiores a la media.

Gráfico de dispersión de Moran (Quadrants of Moran Scatterplot), obtenido de Koutsos et al. (2021)

A este gráfico se añade una recta con pendiente igual al índice de Moran \(I\), tratando de expresar de esta forma una relación lineal con correlación \(I\), de manera que se aprecian aquellos puntos del gráfico que influyen en la recta de regresión construida. Estos son “sospechosos” de autocorrelación espacial, es decir, son posibles puntos calientes.

Si definimos los índices locales de Moran como

\[ \begin{equation} I_i=n \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij} (y_i-\overline{y}) (y_j-\overline{y})}{\sum_{i=1}^n (y_i-\overline{y})^2} \end{equation} \]

se pueden hacer test de zonas locales y contrastar esos puntos sospechosos. Podemos escribir que es

\[ \begin{equation} \frac{1}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}}\sum_{i=1}^n I_i \end{equation} \]

con lo que el valor de \(\sum_{i=1}^n \sum_{j=1}^n w_{ij}\) es una constante de normalización. Podemos decir, por tanto, que con los índices locales de Moran lo que estamos haciendo es descomponer el índice \(I\) global.

3.3.4 Ajuste de modelos

En la mayoría de datos espaciales no habrá independencia, es decir, presentarán autocorrelación espacial. Una forma habitual de modelizar este problema es la de suponer que nuestras observaciones multivariantes \(Y\) (o \(Z\) si seguimos la notación empleada en geoestadística) se pueden expresar en función de covariables de la forma

\[ \begin{equation} Y=\beta_0 + \beta_1X_1 + \cdots + \beta_kX_k + e \end{equation} \]

en donde \(e\) es una variable de error con distribución normal multivariante de vector de medias cero y matriz de varianzas-covarianzas \(V\) (aunque esta modelización podría variar según el modelo considerado, como por ejemplo los modelos autorregresivos, similares a los utilizados en series temporales, capaces de recoger la dependencia espacial de la matriz \(V\)).