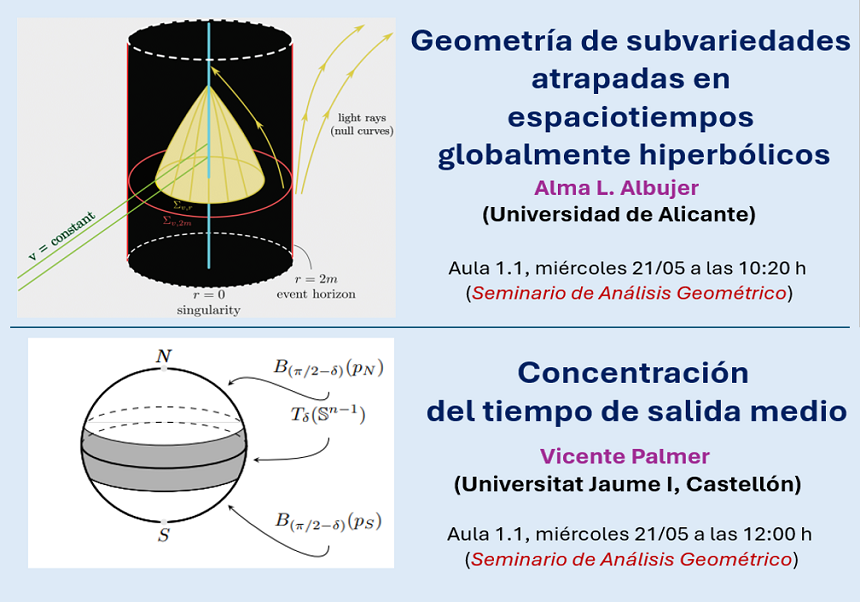
Geometría de subvariedades atrapadas en espaciotiempos globalmente hiperbólicos.

Concentración del tiempo de salida medio

Geometría de subvariedades atrapadas en espaciotiempos globalmente hiperbólicos
Alma L. Albujer
(Universidad de Alicante)
Aula 1.1, miércoles 21/05 a las 10:20 h

(Seminario de Análisis Geométrico)
Resumen: En esta charla mostramos resultados de rigidez y de no existencia de subvariedades espaciales parabólicas, con vector curvatura media causal, en espaciotiempos que admiten una descomposición ortogonal. Estos incluyen, en particular, a la familia de espaciotiempos globalmente hiperbólicos. Por otro lado, también damos un resultado sobre la geometría de una familia más general de subvariedades en dichos espaciotiempos, probando la no existencia de mínimos o máximos locales de una determinada función. Como aplicación en el ámbito de la relatividad general, obtenemos resultados sobre superficies atrapadas (no necesariamente compactas) en una familia muy amplia de espaciotiempos.
Trabajo conjunto con Jónatan Herrera y RafaelM. Rubio (U. de Córdoba).

Concentración del tiempo de salida medio
Vicente Palmer
(Universitat Jaume I, Castellón)
Aula 1.1, miércoles 21/05 a las 12:00 h
(Seminario de Análisis Geométrico)

Resumen: El “fat equator effect” es un fenómeno de concentración de la medida experimentado por las bandas ecuatoriales de las esferas, que se deduce de la desigualdad isoperimétrica de Levy. Conlleva que, si la dimensión de la esfera tiende a infinito, su área se concentra en cualquier banda ecuatorial de radio arbitrario.
En esta charla, estudiamos el comportamiento de la difusión Browniana en la esfera, en términos de la dimensión. En concreto, demostramos que la función del tiempo de salida medio, definida en un tubo de radio arbitrariamente pequeño alrededor de cualquier ecuador, tiende a infinito con la dimensión, de modo que, cuando consideramos una parícula browniana que inicia su movimiento en un ecuador, permanecerá cerca del mismo durante un tiempo casi infinito cuando la dimensión de la esfera se acerque al infinito. Se generaliza esta propiedad a tubos alrededor de
hipersuperficies cerradas y mínimas de una n-variedad Riemanniana compacta M con curvatura de Ricci acotada inferiormente.
Trabajo conjunto con V. Gimeno (UJI) y G. Pacelli Bessa (Ceará-UFC).