Aparato de Galton y esferas de plástico.

El aparato de Galton (también llamado Quincunx), inventado por Sir Francis Galton, primo de Charles Darwin, es un sencillo aparato mecánico formado por una matriz de clavos o tacos dispuestos de forma triangular. Si se dejan caer canicas sobre el taco superior, éstas van rebotando sucesivamente hasta la parte inferior donde se recogen en pequeños contenedores. Cada vez que una canica golpea en un taco puede irse hacia la derecha o hacia la izquierda. Si la probabilidad de que la canica siga un camino u otro es la misma, las canicas recogidas en los contenedores forman una campana de Gauss, alrededor del contenedor central [1, 2].

Se cuenta con dos aparatos de Galton: uno con bolas más del tamaño de canicas (Galton 1) y otro (nuevo) con muchas bolas pequeñas (Galton 2). Según la preferencia particular se pueden llevar a la demostración ambos o solo uno de ellos.

MONTAJE GALTON 1 (fotografías 1 y 2)

Se monta el aparato de Galton. Para ello se insertan las patas azules en la bandeja blanca (la pata marcada con un 1 a la izquierda y la pata marcada con 2 a la derecha). Después se introduce la bandeja azul por la parte superior de la bandeja blanca hasta dejarla apoyada contra la mesa. Las guías de la bandeja azul deben quedar alineadas con los huecos de la última fila de tacos, con el fin de que las bolas puedan caer por dichas guías.

Funcionamiento:

Se van echando las bolas rojas por el embudo superior. Cada bola, en su caída, va chocando contra uno de los tacos de cada una de las nueve filas (fotografía 1), y al final es recogida y almacenada en alguno de las nueve guías de la bandeja azul, según el camino que haya seguido. Cuando se lanzan todas las bolas observaremos un histograma de nueve intervalos correspondientes a las nuevas filas de tacos, y en ellos las bolas que se han ido acumulando (fotografía 2). El número de bolas de cada intervalo se corresponde con la frecuencia asociada a dicho intervalo. 

Para recoger las bolas, se utiliza una bandeja blanca adicional que se sitúa sobre la mesa a continuación de la bandeja azul como se ilustra en la fotografía 2. Si levantamos la regleta blanca que sostiene a las bolas éstas caerán hacia la bandeja de recogida.

MONTAJE GALTON 2 (fotografías 3 y 4)

Se invierte la posición del tablero para que todas las bolitas bajen hasta el triángulo de salida. A continuación se pone la plaquita que viene atada al tablero en la ranura para queden bloqueadas en el triángulo de salida y se gira a la posición de

partida, de manera que el tablero queda apoyado en sus pies y las bolas quedan en la parte superior (fotografía 3). Finalmente se coloca la hoja de papel con la escala en la parte posterior para poder estimar las alturas en cada contenedor

Funcionamiento:

Una vez montado, se retira la plaquita para desbloquear las bolas caigan hacia los compartimentos. Las bolas van cayendo hacia cada compartimento. La hoja que se ha colocado detrás del tablero permite medir la altura relativa en cada compartimento, lo

que se puede usar para hacer una comparación con los valores esperados para la distribución gaussiana si se estima el número de bolitas.

Explicación:

Una bola que se desvíe hacia la derecha n veces acabará en la guía n-ésima contando desde la izquierda. Si el número de filas de tacos es n, la probabilidad de que la bola aparezca en la guía n-ésima es igual a la probabilidad de obtener n desviaciones

hacia la derecha de un total de n ensayos, probabilidad que viene dada por la distribución binomial

siendo p la probabilidad de que la bola se desvíe hacia la derecha en cada choque.

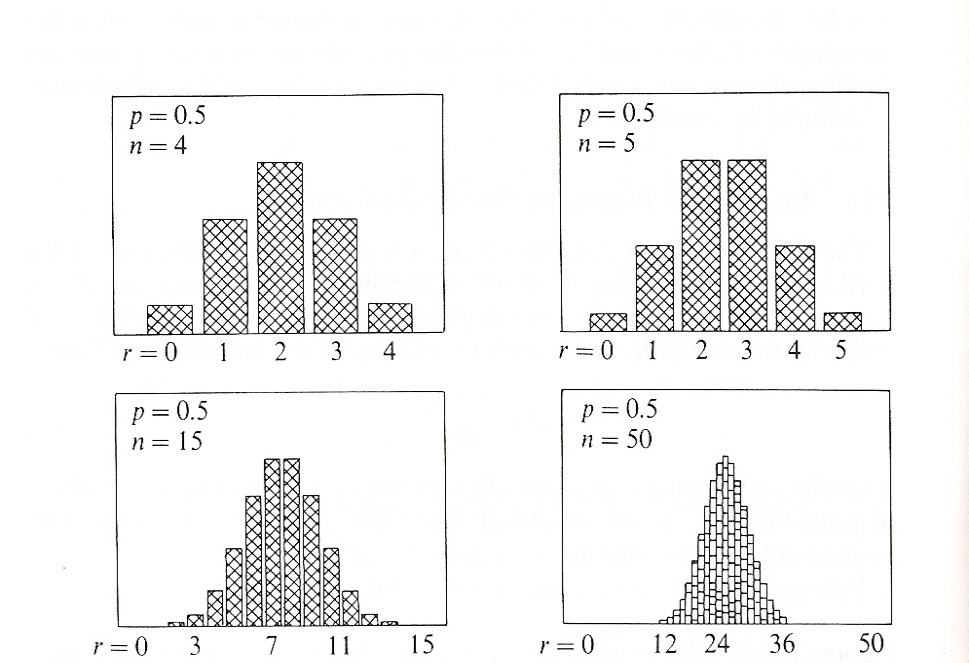
Cuando crece el número de ensayos, esta distribución tiende a una distribución de Gauss de media    y varianza   . En la figura siguiente se observa cómo a medida que crece el número n de ensayos  la distribución binomial (en

este caso con p=1/2) se aproxima mejor a una distribución gaussiana. En realidad p puede tomar cualquier valor, y el resultado sigue siendo una gaussiana  tal y como explica el teorema del límite central)

El proceso de medida de una magnitud física podemos imaginarlo sujeto a un número n grande de fuentes  de error independientes de tipo aleatorio  (efectos de paralaje, tiempos de reacción, etc.), que empujarían con igual probabilidad el resultado  hacia arriba o hacia abajo alrededor del valor verdadero. Al repetir la medida muchas veces los resultados estarían distribuidos de forma gaussiana como consecuencia de la acumulación de un número n grande de errores aleatorios, tal como sucede en el aparato de Galton.

Se puede también animar discutir posibles fuentes de desviación del modelo (bordes limitados, interacción entre las bolas, tridimensionalidad del problema, tamaño no finito de las bolas y los clavos…)

Galton 1: Se pueden contar el número de canicas de cada intervalo para calcular  la media y la varianza, de una distribución particular. Luego se puede estimar  el de esta distribución para cuantificar su grado de similitud con una gaussiana con la misma media y varianza.

Para el Galton 2: se puede hacer la comparación con la gaussiana si se estima en número de bolitas total. Además, se puede “pausar” el proceso poniendo la plaquita en cualquier momento mientras descienden las bolas para mostrar cómo se va formando en pasos sucesivos la distribución gaussiana.

Existen simuladores de estas máquinas [3, 4] que se pueden usar para explorar qué pasa con más estadística, sesgos en la distribución binomial, distinto número de filas, etc.

Galton 1: Se pueden lanzar varias bolas al mismo tiempo por el embudo superior. Al recoger las canicas se ha de ser cuidadoso para que no se pierdan.

[1] Galton, F. (1889). Natural Inheritance. Macmillan
[2] https://es.wikipedia.org/wiki/M%C3%A1quina_de_Galton
[3] https://polypad.amplify.com/lesson/galton-board
[4] https://phet.colorado.edu/en/simulations/plinko-probability