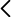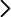La honda y el movimiento circular

Categories:

Mechanics.

Authors:

chantal maria ferrer roca

Tags:

órbita o trayectoria circular, fuerza centrípeta, relación de la velocidad con el radio.

Objectives:

Comprender el concepto aceleración normal o centrípeta en una trayectoria circular y su relación con la velocidad de la órbita y su radio de forma semi-cuantitativa. Observar el fenómeno como un símil de las órbitas planetarias y la relación entre y el radio de la órbita y la velocidad en ella.

Materials:

Masa sujeta a un hilo. Tubo de PVC, tapones de goma de diferente masa mg unidos a hilos con ojal para colgar pesas de diferente masa mp (comprendidas entre 0.2 kg y 0.5 kg y sus combinaciones).

Assembly Time:

1 minuto

Description:

La honda es, en su versión más simple, un cuerpo sujeto a un hilo que gira siguiendo una trayectoria circular, de forma que incluso si su velocidad es constante en módulo, su dirección cambia continuamente. La honda ha sido empleada como arma desde la prehistoria y se usa desde la antigüedad como ejemplo paradigmático del movimiento circular. El lanzamiento de martillo (bola de gran masa unida a un cable) es una prueba de atletismo que se parece al lanzamiento honda, solo que la masa del martillo es mucho mayor que la del proyectil de la honda.

Demostración con una honda sencilla

Puedes probar una honda sencilla haciendo una en casa, con lo primero que encuentres a mano, lo importante es que sea un cuerpo con una masa no muy grande sujeta a un hilo o cable de una cierta longitud. Por ejemplo: un llavero u otra cosa atada a un hilo, una patata dentro de un foulard, un ratón de ordenador viejo con su cable, etc.

La pones a girar encima de tu cabeza con velocidad de giro constante (¡cuidado con tu cabeza y con lo que tengas alrededor!). Sientes la tensión sobre tu mano (igual y opuesta a la tensión que actúa sobre el objeto que gira), mantén siempre aquella que permite mantener el hilo horizontal. Prueba primero usando una longitud de hilo más corta y después otra más larga. En ambos casos debes intentar que la tensión sea la misma (aquella con la que el hilo se mantiene casi horizontal). Observa que el tiempo que dura una vuelta (periodo t) aumenta a medida que alargas la longitud del hilo r.

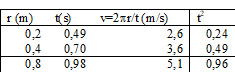La honda y el movimiento circular Con el cronómetro o la videocámara del móvil puedes medir este tiempo o periodo t. Con nuestra honda y para una longitud del hilo r=20 cm se completan 10 giros en 4,9 segundos (t=0,49 s). Hago lo mismo para otras dos longitudes (40 y 80 cm, por ejemplo) 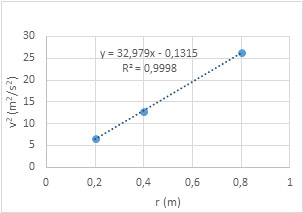y obtengo los resultados de la tabla. Vemos que al multiplicar cuadruplicar la longitud del hilo (r=80 cm), el periodo t se duplica. Calculamos la velocidad y vemos que también aumenta al incrementarse la longitud del hilo r. La representación gráfica de v² frente a r muestra una línea recta cuyo ajuste lineal proporciona un valor de la pendiente de 33 m/s². Esto significa también que la cantidad r/t² es constante (vale 0,8 en ambos casos).

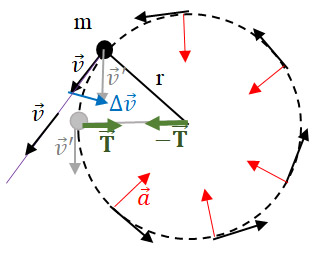La honda y el movimiento circular Explicación: La velocidad $\vec{v}$ del cuerpo, siempre tangente a la circunferencia de su trayectoria, mantiene constante su valor en módulo pero cambia continuamente de dirección. Este objeto seguiría la línea recta si no actuara sobre él la tensión del hilo, una fuerza dirigida hacia el centro del círculo y que continuamente desvía el cuerpo. Por la 2ª Ley de Newton sabemos que la aceleración está relacionada con las fuerzas que actúan. Se ve que la variación de la velocidad $\Delta \vec{v}= \vec{{v}'}-\vec{v}$ , es radial y dirigida hacia el centro de la circunferencia (ver el dibujo). Esta es, pues, la dirección de la aceleración normal o centrípeta $\vec{a}$ que produce ese cambio y también la de la tensión $\vec{T}$ que actúa sobre el cuerpo tirando de él y curvando su trayectoria. Si el hilo se rompe o si el hondero libera el proyectil de su sujeción, desaparece esta fuerza y, por lo tanto, su velocidad permanecerá constante en módulo y dirección y saldrá tangencialmente siguiendo la línea recta.

Recordemos que, por la 3ª ley de Newton, hay una tensión igual y opuesta actuando sobre mi mano en el centro del círculo (la puedo sentir tirando hacia fuera). Por otro lado, como el hilo permanece horizontal supondremos que está en equilibrio en dirección vertical y podemos asumir que la fuerza total en dirección vertical es nula (suma de gravitatoria y componente vertical de la tensión).

Aplicando la 2ª ley de Newton en dirección radial (suma de fuerzas que actúan sobre el cuerpo igual a su masa por su aceleración, todo en esa dirección radial. $\left (a= \frac{v^{2}}{r} = \omega ^{2}r \right )$ . $T= ma=m\frac{v^{2}}{r}= m\omega ^{2}r= mr\left ( \frac{2\pi }{t} \right )^{2}= \left ( 2\pi \right )^{2}m\frac{r}{t^{2}}$ [1]

Por lo tanto, $v= \sqrt{\frac{Tr}{m}}$ . Si no se cambia la tensión ni la masa del cuerpo que gira, la velocidad aumenta con $\sqrt{r}$ , como ya hemos comprobado empíricamente. Si disminuye la masa que gira, a igualdad de las otras magnitudes, la velocidad aumenta. Si aumenta la longitud de la honda, a igualdad de las demás magnitudes, la velocidad aumenta también.

Si no cambia la tensión, la aceleración centrípeta $\frac{v^{2}}{r}$ es constante y también es constante $\frac{t^{2}}{r}$ y se tiene la relación ${t^{2}}= \frac{\left ( 2\pi \right )^{2}m}{T}r$ .

Cualquier movimiento circular funciona de igual forma: si el cuerpo gira cambiando la dirección de su velocidad es porque hay alguna componente centrípeta en la fuerza total que actúa sobre el cuerpo: un vehículo que se mueve por una pista circular lo hace porque actúa el rozamiento de las ruedas en dirección radial (y los pasajeros sentados en el coche siguen el movimiento del coche porque actúa el rozamiento de su trasero con el asiento). Los electrones en un sincrotrón curvan su trayectoria debido a la fuerza magnética que tiene dirección centrípeta, etc, etc. Las órbitas circulares de los astros y planetas, por ejemplo, responden al mismo principio. Si la Luna o un satélite gira alrededor de la Tierra, la Tierra alrededor del Sol o este alrededor del centro de la galaxia es porque actúa una fuerza en dirección radial apuntando hacia el centro del círculo. En este caso, dicha fuerza es la fuerza gravitatoria F_g lugar de la tensión.

Órbitas planetarias circulares: Aplicando como antes la 2ª ley de Newton en dirección radial: $F_{g}= ma=m\frac{v^{2}}{r}$ , solo que ahora la fuerza que actúa es

$F_{g}= G\frac{Mm}{r^{2}}$

donde r es el radio de la circunferencia (la distancia entre la Tierra y el satélite, por ejemplo), M la masa de la Tierra, m la masa del satélite y G la constante de gravitación universal (G=6,67·10^-11 Nm²/kg²)

Luego : $G\frac{Mm}{r^{2}}= m\frac{v^{2}}{r}= mr\left ( \frac{2\pi }{t} \right )^{2}= \left ( 2\pi \right )^{2}m\frac{r}{t^{2'}}$ [2]

Además. $v= \sqrt{\frac{GM}{r}}$ y lo que ahora permanece constante es $\frac{t^{2}}{r^{8}}= \frac{\left ( 2\pi \right )^{2}}{GM}$ (3ª ley de Kepler) [3]

Demostración con una honda unida a una masa que pende verticalmente

Esto se puede hacer con el material de la demostración o bien en casa con cualquier tubo estrecho (como el de aluminio de cocina) y dos cuerpos, uno de menor masa que gira y otro de masa mayor que pende. Este montaje permite controlar la tensión que se aplica a la masa que gira m, ya que queda determinada por la masa de la pesa que se cuelga debajo m_p.

Elegiremos, por ejemplo, como masa que gira el tapón num. 10 (56 g)

Hacer pasar el hilo del tapón elegido por el tubo y colgar por el otro extremo una pesa (de 0,5 kg, por ejemplo). Poner a girar el tapón de goma eligiendo un radio de giro determinado (por ejemplo, r=0,8 m). Ajustar la velocidad de giro de forma que la pesa inferior permanezca en equilibrio. Mientras no cambiemos la masa inferior, la tensión (componente centrípeta de la fuerza) no cambia.

La honda y el movimiento circular

Ahora se puede también cronometrar el tiempo t que tarda en dar 10 vueltas, de forma que f =10/t =1,6 rps. La velocidad angular $\omega = 2\pi f= 10.3 rad/s$ y la velocidad lineal $v=\omega r = 8.2 m/s$ .

Manteniendo el mismo radio o longitud del hilo, aumentar la masa de la pesa inferior : añadir otra pesa de 0,5 kg de forma que haya un total de 1 kg. Poner a girar el tapón. Se verá que se requiere mayor velocidad de giro (concretamente un factor 1,4). O bien, si no aumentamos la velocidad de giro, debemos dejar que el radio aumente.
Ahora elegir un radio menor, por ejemplo de 0,2m, y repetir. Se verá que se requiere una velocidad angular mayor para mantener la pesa inferior en equilibrio. (en este caso deberían darse 3 vueltas por segundo, la velocidad angular debería ser de 19 rad/s y la velocidad lineal debería ser aproximadamente de 3,8 m/s).

En resumen: cuanto mayor es el radio de giro del tapón, menor es la velocidad necesaria para mantener el equilibrio. Cuanto mayor es la pesa inferior (y la tensión), hay que girar el tapón más rápidamente si no se quiere que aumente el radio de giro.

Explicación: En la Figura 2 se representan las fuerzas que actúan en el sistema. Aplicando la 2ª ley de Newton a cada cuerpo, teniendo en cuenta la tensión T del hilo:

Pesa inferior, dir. y : $T-m_{p} g=m_{p}a_{y}$ $\small (a_{y}=0 \: \: en \: equilibrio)$

Tapón que gira (dir. centrípeta) $T=ma_{n}=m\frac{v^{2}}{r}$

Luego, en equilibrio: $\small T=m_{p}g=m\frac{v^{2}}{r}=m\omega^{2}r$ [4]

Es decir, si la pesa está en equilibrio, la fuerza gravitatoria sobre es igual a la tensión T, cuyo valor depende de la velocidad angular (para una m y r dadas). En el caso a) m_pg= 0,5·10= 5 N y coincide con T= m·v²/r= 0.056·(1,7·2·p)²·0.8=5,1 N

Por otro lado, de la expresión [4] se obtiene la aceleración normal cuando la pesa está en equilibrio:

$a_{n}=\frac{v^{2}}{r}=\omega^{2}r=\frac{m_{p}}{m}g=cte$ [5]. proporcional a la masa de la pesa.

También, $\small v= \sqrt{ \frac{m_{p}}{m}gr }\:; \; \; \omega = \sqrt{ \frac{m_{p}}{m} \frac{g}{r} }$ que es proporcional a ${m_{p}^{1/2}}$ (ya verificado) e inversamente proporcional a m y r (como se verifica comparando a) y c) ).

Se puede comprobar que las leyes de Newton predicen correctamente la velocidad angular en el equilibrio:

el valor teórico que se obtiene al calcular con la expresión deducida

$\omega _{teo}=\sqrt{\frac{m_{p}}{m}\frac{g}{r} }= \sqrt{\frac{0,5}{0,056}\frac{9,8}{0,8} }=10,5\: rad/s$

el valor medido (experimental) :

$\omega _{exp}=\frac{2\pi }{\tau _{exp} } =2\pi f_{exp}=10,5\: rad/s$

ESTA DEMO PUEDE UTILIZAR COMO UN SÍMIL DE ÓRBITAS CIRCULARES GRAVITATORIAS

El objeto que gira se asemeja a un planeta de masa m en una órbita circular alrededor de una estrella de masa M, y la tensión del hilo representa la fuerza gravitatoria que dicha estrella ejerce sobre el planeta.

Podemos considerar un planeta que gira en una órbita de radio r₁ y otro que lo hace a r₂=2 r_{1 .}Para simular que actúa una fuerza gravitatoria diferente sobre cada uno (ya que la fuerza disminuye con el cuadrado de la distancia), se puede cambiar la masa inferior, de forma que la tensión que actúa sobre el “planeta” más alejado disminuya en la proporción adecuada:

Para r₁ T₁= m·(GM /r₁²)= m_p g (usar 0,8 kg, por ejemplo)

Para r₂=2r₁: T₂= m·(GM /r₂²)= T₁/4= m_pg/4 se requiere una pesa que tenga una masa 4 veces inferior.(0,2 kg)

Como hemos visto, en las órbitas gravitatorias circulares lsegún la 2ª ley de Newton, la velocidad viene dada por:

$v= \sqrt{\frac{GM}{r}}$

Luego si r₂= 2r₁ entonces v₂= v₁ /2^1/2 Veamos que esto se cumple en nuestra “simulación” de las órbitas circulares:

m_pg/4 = m v₂² /r₂= m v₂² /2r₁ luego v₂² /2r₁= v₁² /4r₁ y v₂= v₁ /2^1/2

También se puede verificar la tercera ley de Kepler: la relación entre los periodos orbitales medidos cumple es

Comentaris:

Como hay un conjunto completo de tapones de goma que pueden girar y también de pesas, se puede hacer un desarrollo experimental más amplio. Es decir, realizar diferentes medidas en las que se varíe el radio (tomar varios valores), o la masa de gira m o la pesa inferior m_p , verificando las dependencias discutidas.

Nota histórica

La piedra girando en la honda como símil del movimiento en órbitas circulares se encuentra citado en varios textos antiguos, por ejemplo, en el “De facie quae in orbe lunae apparet”, 7 [923 F-924 C]” (sobre la cara visible de la Luna) de Plutarco, intelectual griego que vivió en el último periodo republicano romano (s. I AC):

“A la Luna le impide caer su propio movimiento y la rapidez de su revolución, al igual que el proyectil de la honda no cae debido a su giro circular. Ya que el movimiento natural guía todas las cosas, salvo que algo las desvíe. Por eso la Luna no sigue su peso: la influencia de éste queda anulada por la acción del movimiento orbital”

Los conocimientos de física y matemáticas de esta época se encuentran en recopilaciones mal comprendidas del trabajo de científicos del periodo helenístico, de siglos anteriores (s. IV-II AC), en los que tuvieron lugar importantes desarrollos en ciencia y tecnología. Para más información.

File:

Demo 116 en pdf

Demo 116. La honda y el movimiento circular