Base con circuito metálico que incluye un rizo y dos bolas de acero

Se suelta la bola de acero desde una posición del plano inclinado comprendida entre las dos marcas blancas. Se observa que la bola desciende por el plano y al llegar al rizo o loop da la vuelta completa sin caerse, hasta llegar al tope final del circuito. Si se deja caer por debajo de la marca inferior, antes de llegar al punto más alto del rizo, la bola cae, y no completa el loop. Por encima de la marca superior, la bola se sale del raíl y hace caída libre.

Explicación: supongamos que solo actúa la fuerza gravitatoria y la fuerza de contacto de la bola con el carril. La energía mecánica en el punto inicial (A) es sólo energía potencial gravitatoria. En el punto (B) es potencial gravitatoria y cinética. 

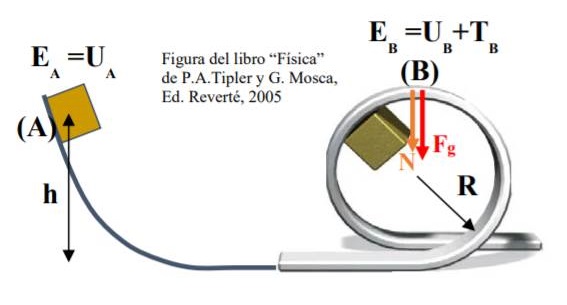
Por conservación de la energía mecánica en A y B, se cumple en general:   [1]

Aplicando la 2ª ley de Newton en dirección normal (radial sentido hacia el centro de la circunferencia) en el punto B tenemos:

           [2]

Vemos a partir de [2], que la velocidad será mínima cuando la fuerza de contacto N entre la bola y la superficie sobre la que se apoya es nula (N=0, ingravidez )

     [3]

Luego habrá una altura mínima h_min inicial que produzca la velocidad mínima vmin en el punto B. Sustituyendo en la conservación de la energía [1] :

[4]

Luego    independiente de m .

Si, además, actúa algún tipo de fuerza disipativa (rozamiento con el aire), en la parte derecha de [1] se añade el trabajo W de dicha fuerza, por lo que . Es decir, hay que soltar la bola desde una altura mayor de la calculada inicialmente.

Ver los vídeos adjuntos:

Movimiento por un loop (conservación E) y Corredor completa un loop sin caerse.

• Movimiento por un loop (conservación E)
• Corredor completa un loop sin caerse