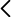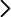- Tubo de difracción de electrones.
- Fuente de alimentación para la extracción y focalización de los electrones.
- Fuente de alimentación aceleradora (de 0 a 10 kV).
- Webcam para proyección de imágenes.
IMPORTANTE: Esta demostración está montada en un carro para su transporte a las aulas, ubicado en el laboratorio de Física Cuántica. Para recogerlo, contactar con el prof. Pedro González
Descripción El equipo de difracción de los electrones, figura 1, se compone de un tubo de rayos catódicos, en el que se ha hecho el vacío, y en el cual los electrones se extraen de un filamento incandescente por efecto termoiónico. Los electrones son acelerados por una diferencia de potencial de hasta 7 kV y focalizados sobre un blanco de grafito. Los electrones son dispersados por los microcristales del grafito y alcanzan la pantalla fosforescente esférica del tubo donde producen centelleo. Los microcristales tienen todas las posibles orientaciones, por lo que no hay una dirección privilegiada de dispersión de los electrones por el grafito alrededor del haz de los electrones. Debido a esta simetría axial, las dispersiones de Bragg del haz de electrones dan lugar a anillos de interferencia constructiva sobre la pantalla fosforescente, en la que cada punto luminoso resulta del impacto de un electrón. El dispositivo experimental permite observar con nitidez estas interferencias (véanse figuras de cabecera de este documento). Las dispersiones de Bragg, así como la formación de anillos, a partir de las mismas, están explicadas detalladamente en el guion que acompaña a esta ficha. La dispersión de Bragg de los electrones es un fenómeno relacionado con la naturaleza ondulatoria del electrón, cuya longitud de onda de De Broglie está dada por la ecuación (1), en la que ℎ es la constante de Planck (h = 6,626 × 10−34 J. s.) y p es el momento lineal del electrón. El electrón se acelera con una diferencia de potencial máxima de 7 kV, por lo que su energía cinética máxima será de 7 keV. Esta energía es significativamente inferior a la masa del electrón (mc2 = 511 keV), lo que permite considerar el movimiento del electrón no relativista, y calcular su longitud de onda de de Broglie usando las ecuaciones (2) y (3).
(1)
(2)
(3)

La condición de interferencia constructiva de los rayos de electrones dispersados por planos atómicos paralelos del grafito con distancia interplanar d, para ángulos de incidencia iguales, se expresa mediante la condición de Bragg, ecuación (4).
(4)
Esta estipula que debe de haber una diferencia de caminos recorridos por los rayos de un número entero de longitudes de onda del electrón, donde n es el orden de interferencia de los rayos, y n=1 el orden observado con más intensidad. En el tubo de rayos catódicos (figura 2), el diámetro d del anillo de interferencia, para un ángulo de difracción 𝜃, está dado por la ecuación (5).
(5)
donde L= 130 mm es la distancia entre el blanco de grafito y la pantalla fosforescente. Considerando las distancias interplanares 𝑑1 = 123 𝑝m y 𝑑2 = 213 𝑝m (figura 3) citadas en la literatura [2-3], se deducen de las ecuaciones (4) y (5) los diámetros de los anillos de interferencia de primer orden (𝑛 = 1) y
. Estos son los anillos de más intensidad observables en la pantalla fosforescente. Los anillos de orden superior se observan con mucho menos intensidad.
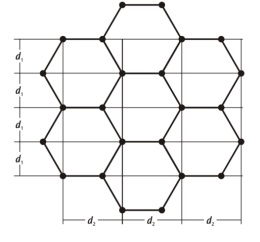
Figura 3: Esquema de la red cristalina del grafito, en donde se aprecian los átomos de carbono formando
hexágonos, y los planos atómicos a las distancias d1 = 123 pm y d2 = 213 pm en los cuales se
produce la dispersión de los electrones y las interferencias constructivas.
Para observar los anillos de difracción de los electrones en la pantalla fosforescente del tubo catódico, se debe elegir en la fuente aceleradora un voltaje de unos 5-6 kV, que corresponde a girar el botón regulador del voltaje hacia la derecha, desde el cero (ver Figura 4). Poner a 0 los botones controladores de la fuente focalizadora G1 y G4 para conseguir un haz fino. Una vez visualizados los anillos se puede observar cómo varía el tamaño de los anillos al hacerlo el voltaje acelerador. Para ello conviene fijarse en un anillo concreto. Al subir el voltaje el tamaño del anillo decrece. Ello está relacionado con el hecho de que, según la relación de De Broglie, la longitud de onda de los electrones disminuye al aumentar su momento (es decir, al aumentar el potencial acelerador aplicado a los mismos), por lo que el ángulo de Bragg disminuye. Se puede comprobar que los impactos en la pantalla corresponden a partículas cargadas acercando un imán y observando la deformación de los anillos. Para una demostración cuantitativa de la difracción de Bragg, se puede medir los radios de los anillos y utilizando las distancias interplanares en el grafito, se puede comprobar la Ley de Bragg, para cada voltaje acelerador. A la inversa, a partir de las medidas de los radios y de los voltajes aceleradores se pueden extraer las distancias entre planos atómicos paralelos en el grafito. Se propone a continuación un ejemplo práctico de la demostración para dos voltajes de aceleración. Los voltajes de aceleración de los electrones que permite el equipo de difracción se muestran en la Figura 4, junto con las correspondientes longitudes de onda de De Broglie de los electrones acelerados. En el equipo se dispone de un sistema de focalización con voltajes y límites que se describen en la documentación del equipo [1].
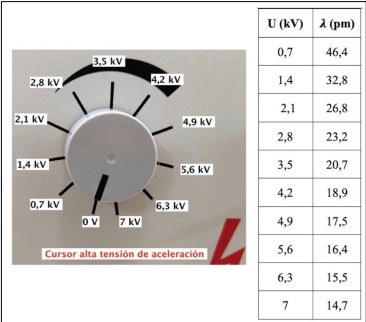
Figura 4: Tabla de voltajes de aceleración y longitudes de onda de De Broglie. A la izquierda de la imagen se indican las posiciones del cursor y los valores correspondientes del voltaje de aceleración.
Para un voltaje de aceleración U, se puede medir el diámetro de los anillos observados en la pantalla fosforescente, utilizando un pie de rey y compararlo con el diámetro de los anillos de Bragg mencionados.
En la Figura 5 se muestran los anillos de diámetro 𝐷1 y 𝐷2 medidos con el pie de rey, con una incertidumbre derivada del grosor de unos 4 mm de los anillos. En la tabla 1, se recogen los valores de los diámetros medidos para los voltajes de aceleración de 4,9 kV y 7 kV, así como los valores de los diámetros determinados por la condición de Bragg. Como se puede ver en esta tabla, los valores experimentales de los diámetros de los anillos de interferencia de primer orden son compatibles con los valores calculados por la ecuación de Bragg (4). Se observa también que a mayor voltaje menor diámetro de los anillos.

Figura 5: Anillos de interferencia de diámetro D1 y D2 correspondientes a las distancias inter-planares de los microcristales del grafito d1 = 123 pm y d2 = 213 pm, respectivamente, para un voltaje de aceleración de 7 kV.

electrones para dos voltajes de aceleración.
Aunque el experimento puede hacerse en penumbra y a la vista directa de los alumnos, resulta práctico, una vez explicado el funcionamiento, tapar el tubo y proyectar, en la pantalla del aula, los anillos mediante una webcam. Aparte de evitar la aglomeración de estudiantes en torno al experimento, la condición de oscuridad hace que los anillos se vean nítidamente. Para ello se dispone de una tela negra que cae sobre una pared transparente de metacrilato a la misma altura que las fuentes, pero en el extremo opuesto de la mesa experimental. Así se pueden manipular las fuentes de alimentación lateralmente mientras las imágenes nítidas de los anillos aparecen proyectadas. Se aconseja para la medición de los diámetros de los anillos evitar exponer excesivamente las manos en la zona de medición de la pantalla fosforescente, pues en ésta se producen rayos X.
1- https://www.phywe.com/experiments-sets/nobel-prize-experiments/electrondiffraction_9532_10463/
2- D Gray, A McCaughan, B Mookerji, Cristal structure of Graphite, Graphene and Silicon. Physics for Solid State Applications 6, 730. 2009
3- S. Hembacher et al., Revealing the hidden atom in graphite by low temperature atomic force microscopy. https://doi.org/10.1073/pnas.2134173100