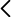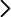Varilla que gira con pesas en los extremos

Categories:

Mechanics.

Authors:

domingo martinez garcia , chantal maria ferrer roca

Tags:

Rotación del sólido rígido, momento de fuerzas, aceleración angular, momento de inercia.

Objectives:

Ilustrar cualitativa y cuantitativamente los conceptos básicos involucrados en la dinámica de rotación de un sólido rígido, midiendo velocidad angular, aceleración angular y poniendo de manifiesto el papel que juega el momento de inercia en la dinámica de rotación de un sistema.

Materials:

Base con eje de rotación y husillo, hilo, soporte con polea, varilla hueca de acero, pesas de disco (100 y 200 g), fijadores de pesas de plástico, gancho portapesas y pesa ranurada de 10g.

Assembly Time:

5 minutos.

Description:

En primer lugar se monta la base con el eje de rotación en la mesa, sujetando la varilla con las pesas de disco en el eje. Poner las pesas de disco a una distancia R = 25 cm del eje (posición extrema marcada en ,la varilla para los fijadores de plástico). A continuación se enrolla el hilo en el husillo poniendo en el extremo el gancho porta-pesas, con la pesa de 10 g. La base de la polea se coloca al borde de la mesa y se hace pasar el hilo por la polea de manera que la pesa cuelgue verticalmente. Procurad que el hilo quede perpendicular al husillo en la parte horizontal y que no roce con la mesa en la vertical (tal y como ilustran las figuras de arriba). Al dejar caer libremente la pesa hacia abajo el hilo se desenrolla del husillo haciendo girar el sistema varilla-pesas.

La dinámica del sistema se puede describir con las siguientes ecuaciones:

$r\cdot T=I\cdot \alpha\:\:\:\:\:\:\:\: (1)$
$mg-T=ma\: \: \: \: \: (2)$
$a = r\cdot\alpha \: \: \: \: \: \: \: (3)$

Siendo r el radio del husillo, T la tensión del hilo, I el momento de inercia del sistema varilla-pesas, a la aceleración angular, a la aceleración lineal de la pesa colgante y m su masa (incluida la masa del portapesas).Combinando las ecuaciones anteriores se puede obtener la siguiente expresión para la aceleración angular:

$\alpha = \frac{rmg}{I + mr^{2}}$ (4)

que en la aproximación I >> mr² se puede escribir como: $\alpha \approx \frac{rmg}{I}$ (5)

que podemos interpretar como si el momento de fuerzas que hace girar el sistema varilla-pesas lo generara la fuerza gravitatoria (mg) de la pesa que cae verticalmente. Esta ecuación pone de manifiesto que hay una relación inversamente proporcional entre la aceleración angular del sistema y el momento de inercia, que vamos a comprobar experimentalmente. Mediremos la aceleración angular para dos valores del momento de inercia (cambiando la distancia de las pesas al eje).

El momento de inercia se puede calcular con la expresión: $I = I_{varilla} + I_{pesas} =\frac{1}{12}\cdot M_{var}L^{2} + 2M_{pesa}R^{2}$ (6)

Aproximando las pesas como masas puntuales, y siendo L la longitud de la varilla y R la distancia de las pesas al eje de giro. Teniendo en cuenta que M_varilla = 114,2 g, L = 60 cm, M_pesa = 300 g y si consideramos dos distancias al eje R₁ = 25 cm y R₂ = 12,5 cm, se puede obtener el momento de inercia, para cada una de las situaciones utilizando la ecuación (6) :

I₁(R₁) = 40,9∙10^-3 kg∙m²

I₂(R₂) = 12,8∙10^-3 kg∙m²

Se pueden comparar con mr² : m = 10 g (10 g del portapesas y otros 10 g de la pesa gris) r ≈ 1 cm, con lo que mr² = 2∙10^-6 kg∙m², es decir, cuatro o cinco órdenes de magnitud menor que I, lo que justifica la validez de la aproximación en la ecuación (5).

A partir de la ecuación (5): al disminuir R, disminuye el momento de inercia I, y por lo tanto aumenta la aceleración angular, es decir $\alpha$ ₂ > $\alpha$ ₁. La relación teórica entre las aceleraciones angulares $\alpha$ ₁ e $\alpha$ ₂ que se obtiene a partir de la relación (5) y los datos es:

$\left.\begin{matrix} \frac{a_{2}}{a_{1}} \end{matrix}\right|_{teo}= \left.\begin{matrix} \frac{\alpha _{2}}{\alpha _{1}} \end{matrix}\right|_{teo}= \left.\begin{matrix} \frac{I _{1}}{I _{2}} \end{matrix}\right|_{teo}= 3,1$ o, lo que es lo mismo $\alpha _{2}^{teo} \approx 3,1 \alpha _{2}^{teo}$ (7)

Ahora vamos a realizar medidas para obtener los valores experimentales. Hay dos procedimientos: medir la aceleración angular a partir de la velocidad angular inicial y final, o bien medir el tiempo de descenso de la masa.

MÉTODO 1

Un o una estudiante cronometra el tiempo de caída de la masa desde el instante en que se suelta la barra hasta el que la masa toca el suelo en las dos situaciones: con las pesas en la posición más externa (1) y más interna (2). La distancia vertical recorrida por la masa en ambos casos es $h= \frac{1}{2}a_{1}\Delta t_{1}^{2}= \frac{1}{2}a_{2}\Delta t_{2}^{2}$ . Luego se cumple que:

$\left.\begin{matrix} \frac{a_{2}}{a_{1}} \end{matrix}\right|_{exp}= \left.\begin{matrix} \frac{\Delta t _{1}^{2}}{\Delta t _{2}^{2}} \end{matrix}\right|_{exp}= \frac{32,3^{2}}{57,9^{2}}= 3,2$

Este resultado coincide con la predicción teórica dentro del margen de incertidumbre (7), lo que indica que el modelo de sólido rígido es adecuado. Hay que tener en cuenta, además, que se ha obtenido asumiendo varias aproximaciones (pesas como masas puntuales, vástago como varilla, poleas de masa despreciable, ausencia de rozamientos, etc.)

MÉTODO 2:

Dos estudiantes estarán preparados con sendos cronómetros.
Suelte el gancho con las pesas.
Un estudiante cronometrará el tiempo que tarda la masa en llegar al suelo (Dt).
En cuanto la masa toque el suelo, el siguiente estudiante cronometrará el tiempo que tarda el sistema en dar dos vueltas (t) (para ello se ha puesto una marca de referencia en una de las pesas de disco). Al tocar las pesas el suelo, el hilo deja de tener tensión y por lo tanto la aceleración angular se hace cero y el sistema gira con velocidad angular constante, salvo por el rozamiento. Por ello hay que hacer la medida antes de que el rozamiento amortigüe el movimiento.

Con estas medidas se puede calcular la $\omega _{final}$ , y $\alpha$ , ambos experimentales (obetnidos a partir de las medidas de los tiempos siendo $\Delta \omega =\omega_{f}$ : (la velocidad angular inicial es cero). $\omega _{\int exp}=2 \frac{2\pi }{t} \, \, \, \,\; \; \; \; \; \; \, \, \, \, \, \, \, \alpha ^{exp}=\frac{\Delta \omega }{\Delta t}$

Luego para R₁ = 25 cm, se obtiene un determinado valor de la aceleración angular a_1:

Repetimos la medida reduciendo la distancia de las pesas al eje de giro a la mitad, es decir para un valor R₂ = 12,5 cm, se obtiene un valor $\alpha$ ₂ para la aceleración angular. $\alpha ^{exp}_{2}=\frac{\Delta \omega_{2} }{\Delta t_{2}} = \frac{4\pi}{t_{2}\Delta t_{2}}$

Tras la medida, se verifica que los valores experimentales coinciden con la predicción teórica dentro del margen de incertidumbre: $\frac{\alpha ^{exp}_{2}}{\alpha ^{exp}_{1}} = \frac{t_{1}\Delta t_{1}}{t_{2}\Delta t_{2}}\approx 3,\! 1$

Comentaris:

- En función del tiempo disponible se puede hacer un experimento más completo. Por ejemplo, medir la aceleración angular para más valores de la distancia de las pesas al eje de rotación. O bien estudiar la influencia de la masa m, para un valor fijo del momento de inercia I. Para ello se dispone de una pesa ranurada roja, adicional, de 20 g.

- La ecuación (5) tiene una utilidad adicional: determinar el momento de inercia desconocido de un cuerpo arbitrario mediante una recta de regresión de puntos experimentales, siendo a la ordenada, m la variable (se cambian las masas que penden del portapesas), y gr/I la pendiente

$\alpha \approx \frac{gr}{I} \cdot m$ (5)

Video gallery:

Varilla que gira con pesas en los extremos

File:

Demo 137 en pdf

Demo 137. Varilla que gira con pesas en los extremos