
Anabel Forte Deltell, Universitat de València
Imaginem que, en despertar-nos, sentim en la ràdio una notícia urgent: “S'ha alliberat un virus que converteix les persones en zombis i que es transmet mitjançant una mossegada”. Què podem fer?
Les opcions són variades. Podem tancar-nos en casa amb pany i clau i esperar que no vinguen infectats o eixir corrent al camp i fugir lluny, molt lluny, a algun refugi on no ens trobe ningú. Cada estratègia té els seus avantatges i els seus inconvenients, i molts factors determinen quina és la millor. Podria un zombi trencar la porta de casa? Correrà prou per a agafar-nos al camp? Quants en trobarem de camí cap al refugi? Quant tardarem a transformar-nos si ens mosseguen? N’hi ha cap cura?
Existeix una solució alternativa: recórrer a les matemàtiques i a l'estadística per a escapar-nos-en. Gràcies a les matemàtiques podem modelitzar el comportament de l'epidèmia mitjançant allò que es coneix com a models SIR.
A grans trets, un model SIR és un sistema d'equacions diferencials que permet comprendre la dinàmica d'una infecció. En concret, com variarà en el temps el nombre de persones susceptibles de ser infectades (S), el nombre d'infectades (I) i el de recuperades (R).
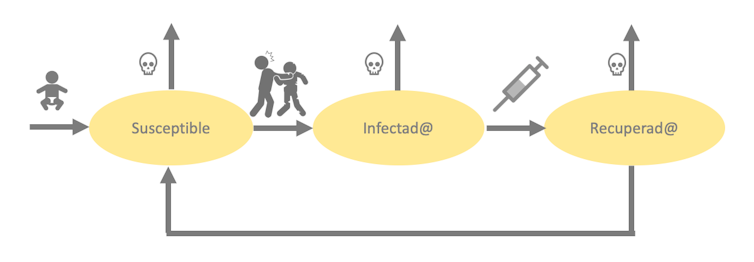
Representació d'un model SIR per a l'epidèmia zombi.
Per a poder comprendre una epidèmia hem de conèixer com es transmet i quines variables hi influeixen. Com es passa de ser susceptible a estar infectat? I a estar recuperat? Es pot tornar a ser susceptible després d'una recuperació? Es pot eixir del sistema de cap altra forma que no siga per defunció?
Per a respondre a aquestes preguntes hem de conèixer bé l'epidèmia. Per sort per a nosaltres encara no coneixem les dades d'una infecció zombi, però aquests models són útils per a entendre’n moltes altres, com la grip, la varicel·la i l'ebola.
En realitat, existeixen models matemàtics per a entendre quasi tots els aspectes de la vida. Models econòmics, models físics, models climàtics, models biomèdics. N'hi ha de totes les formes i nivells de complexitat i ens serveixen per a entendre on cal invertir, com batega un cor i com podem fugir del flux piroclàstic d'un volcà.
Però –sempre hi ha un però– tots aquests models pateixen del mateix inconvenient. Són una manera de representar el nostre coneixement respecte a un fenomen que és, quasi sempre, incomplet. Això deixa un buit entre el model i la realitat que volem explicar. Per aquest buit s’esmuny l'estadística.
Arribats a aquest punt, estic quasi segura que esteu pensant “Estadística? De veritat? Però no és allò de les enquestes?”. Potser us han vingut al cap paraules com dades o gràfiques. Però l'estadística és molt més que tot això.
L'estadística es troba darrere de cada nou tractament mèdic, de l'eficàcia de cada vacuna, de cada nou fertilitzant. També es troba al darrere de moltes polítiques mediambientals, de la recomanació de no fumar i de la que les embarassades i els menors de deu anys no consumisquen tonyina i emperador. Dit d'una altra forma, l'estadística és la ciència que ens permet entendre tot allò a què el nostre coneixement no arriba, per a quantificar la incertesa que ens envolta.
Tornem al cas dels models matemàtics. La metodologia estadística permet captar allò que difereix entre el procés real i el simulat i donar-hi forma. Per entendre-ho millor, penseu en una reacció química. Volem saber com de ràpid es produeix i un expert ens dona una fórmula que ens permet estimar aquella velocitat a partir de la quantitat de producte sense reaccionar en cada instant de temps. Així que repetim tres vegades la reacció, la mesurem en diversos instants de temps i obtenim una aproximació al valor desitjat.
Fins ací tot genial, però –maleït però– en la fórmula no s'ha tingut en compte que sempre hi ha una part del producte que no reacciona perquè es queda enganxat a les parets del recipient. Amb aquest panorama és molt possible que el valor de la velocitat que hem estimat siga erroni.
Ho podem veure en la següent gràfica, on els punts representen la quantitat de producte sense reaccionar en cada instant. La línia roja és el model incorrecte i la verda representaria el correcte. El primer estima que la taxa de reacció (velocitat) és de 0,63 quan, en realitat, és de 1,7.
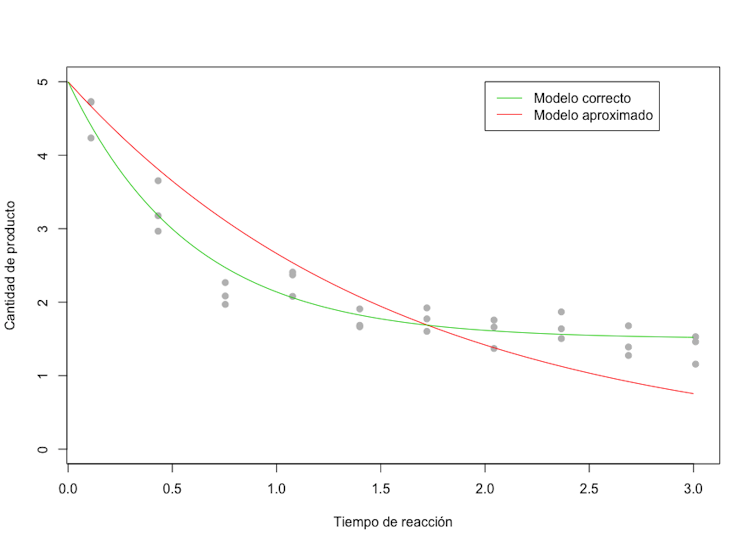
Evolució de la reacció química.
Què fem aleshores? Com podíem saber que el model estava malament? En realitat, no podíem, però sí que podem afegir al model una correcció estadística, alguna cosa que només tinga efecte quan el que observem diferisca del model. Aquesta correcció se la coneix com a funció de discrepància i, en aquest exemple concret, permet recuperar una estimació del paràmetre en 1,72 (quasi l’hem encertada!).
Tenir en compte que hi ha incertesa, fins i tot sobre el model que estem utilitzant, és fonamental per a aconseguir millors resultats.
Arribats fins ací, com ajuda això a fugir dels zombis? (No me n'havia oblidat.) Doncs fàcil: afegir aquesta funció de discrepància al model SIR permet (si hi ha dades) estimar millor la velocitat de pas dels monstres, quant tardem a infectar-nos després de la mossegada i l'eficàcia de la cura. Així, l'estadística ens ajuda a decidir on és millor amagar-nos.
Anabel Forte Deltell, Doctora en Matemàtiques i professora en la Universitat de València, Departament d'Estadística i Investigació Operativa, Universitat de València
Este artículo fue publicado originalmente en The Conversation. Lea el original.

.jpg)








