
Pablo Beltrán-Pellicer, Universidad de Zaragoza; Gregorio Morales Ordóñez, Universitat de València i Sergio Martínez-Juste, Universidad de Zaragoza
Pensa en matemàtiques i, més concretament, en la classe de matemàtiques: has pensat en operacions, fórmules i exercicis? És l'habitual. I, tot i això, tenen molt més a veure amb raonar, comunicar, resoldre problemes, representar. Posar el focus de l'ensenyament en l'un o l'altre cantó afecta de manera diferent les emocions, l'autoconcepte (si pensem que hi tenim facilitat o no) i les creences de l'alumnat respecte a les matemàtiques.
Hem investigat aquestes tres dimensions (emocions, autoconcepte i creences) quan les classes de matemàtiques passen de tenir un enfocament “instrumental” (basat en regles i procediments aplicats sense significat) a un de “relacional” (fonamentat en una comprensió profunda dels continguts). I hem comprovat que el segon permet a l'alumnat viure l'assignatura d'una manera més positiva, sentir-se més competents en matemàtiques i construir una visió més rica de què significa fer-les.
Si és objectivament millor, per què és tan difícil d'adoptar aquest model en la classe de matemàtiques? Els avanços curriculars, les orientacions internacionals i la bibliografia científica incideixen en la seua importància, però el professorat sovint prefereix repetir models d'ensenyament similars als que va experimentar en el seu moment com a estudiant, i els llibres de text no solen afavorir aquest enfocament.
Un punt de partida instrumental
N’hi ha prou fent una ullada als llibres de text habituals per a comprovar que l'ensenyament de les matemàtiques, tant en primària com secundària, continua estant marcat per un enfocament instrumental: “Això es fa així, exercita, repeteix”.
Això és precisament el que ens trobem en analitzar redaccions d'un grup de 19 estudiants al començament de quart de primària: la majoria descrivia les matemàtiques com una assignatura centrada en operacions. “Els problemes són multiplicacions, sumes, restes…”, escrivia un alumne.
En aquestes redaccions, els alumnes percebien la seua competència en matemàtiques com a baixa. Les emocions, quan eren positives, es limitaven a un “M'agraden” sense més profunditat. El missatge era clar: les matemàtiques eren exercicis aritmètics rutinaris que calia superar. No es feien referències al raonament i a la comprensió.
El gir cap a la resolució de problemes
En un model d'ensenyament instrumental es fomenta una comprensió superficial dels continguts, perquè l'aprenentatge d'aquests requereix memoritzar una sèrie de regles. Qui no ha sentit mai la frase “No cal que ho entengues ara: simplement fes-ho”? Fins i tot en pel·lícules com ara Omohide Poro Poro (‘Records gota a gota’, exhibida a l’Estat espanyol com a Recuerdos del ayer (1991)) apareix aquesta tendència.
Les tasques a fer solen ser rutinàries, exercicis, mentre que els problemes es redueixen moltes vegades a exercicis amb un context que actua com a decorat, sense aportar res. És possible que en aquest model apareguen problemes autèntics al final, que comporten un repte i per als quals no hi haja una regla directa de resolució.
Ben al contrari, en un model relacional es persegueix una comprensió profunda dels continguts. L'objectiu ja no és aprendre's una sèrie de regles sense significat, sinó connectar l'experiència prèvia per construir coneixement nou.
Per fer-ho, és imprescindible mobilitzar processos que indiquen activitat matemàtica de qualitat: resolució de problemes; raonament, conjectura i prova; argumentació; comunicació; representació; connexions dins i fora de les matemàtiques. L'aprenentatge per mitjà de la resolució de problemes implica que l'alumnat s'enfronta a problemes autèntics, acuradament seleccionats, sense haver rebut instrucció prèvia que els convertisca en exercicis. És en la resolució d'aquests problemes, amb l'adequat suport de la teoria de la bastida per part del professorat (normalment en forma de preguntes), on emergeix el nou contingut.
Per exemple, calcular l'àrea un quadrat “inclinat” en una quadrícula, és tot un problema. Si no es coneix el teorema de Pitàgores, clar:
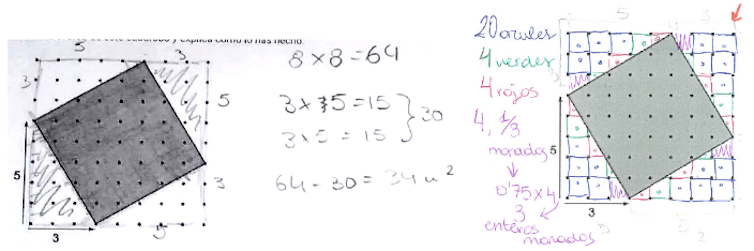
En la imatge podem veure dues tècniques posades en joc per l'alumnat per a resoldre'l. Aquest problema dona lloc a una extensió directa, perquè si es planteja investigar l'àrea de quadrats amb diferents “inclinacions”, la generalització et posa en safata el famós teorema. Observem que si primer es proporciona el teorema, com es faria en un model instrumental, el problema es converteix en un exercici rutinari.
Treballant amb l'enfocament relacional
Al llarg del curs, el nostre grup de 19 estudiants va treballar amb un model relacional, centrat en la resolució de problemes i en metodologies com les thinking classrooms, també conegudes com a aules per a pensar, que sorgeixen arran d'un llibre del professor suec Peter Liljedahl. En aquesta obra es recull una sèrie de tècniques que facilita la creació d'una cultura d'aula orientada a la resolució de problemes. Per exemple, que l'alumnat s'hi enfronte dret, en pissarres esborrables verticals i en grups aleatoris de tres. D'aquesta manera, la interacció es multiplica, al mateix temps que el docent es fa més conscient de què està fent l'alumnat.
El canvi va ser radical. Al juny, 15 dels 19 alumnes parlaven de les matemàtiques com una cosa que tenia a veure amb comprendre, pensar, treballar en grup i trobar sentit. Ja no es tractava de comptes, sinó de processos. Una xiqueta resumia així la seua experiència:
“Les matemàtiques per a mi són poder entendre els nombres. M'agrada treballar en grups en les pissarres en comptes de fer-ho en solitari”.
Aquest canvi d'enfocament no sols va transformar la visió de l'assignatura. També va augmentar l'autopercepció de competència: sis estudiants se sentien ara “bons en matemàtiques”, enfront de només un a l'inici. I en el pla emocional, 16 de 19 expressaven entusiasme, diversió i tranquil·litat, i vinculaven les seues emocions positives amb activitats concretes, com ara resoldre problemes difícils o col·laborar en grup.
L'aula va deixar de ser un lloc on es repeteixen procediments per a convertir-se en un espai d'exploració i descobriment compartit.
El retorn al model expositiu
La història, tanmateix, no acaba ací. Al gener del curs següent, ja en cinquè de primària, aquest mateix alumnat va tornar a un enfocament instrumental, basat en exercicis individuals i ensenyament expositiu. Vam tornar a demanar redaccions al principi de curs en què compartissen les seues emocions i creences sobre l'assignatura. El contrast va ser immediat. Menys de la meitat de les redaccions incloïen ara una visió clara de les matemàtiques, i moltes reflectien avorriment o descoratjament, com indica un alumne:
“Enguany les mates són més avorrides perquè la majoria de les vegades fem comptes”.
Curiosament, la percepció de competència continuava sent alta: 12 alumnes se sentien segurs. Però les emocions es van tornar negatives per als qui havien gaudit d'un aprenentatge relacional. La incoherència entre el que havien viscut abans i el que ara trobaven en classe generava frustració.
Alhora, un altre grup d'estudiants mostrava alleujament: “No tenim quasi cap problema difícil… M'agraden les matemàtiques”. Per a alguns, la baixa demanda cognitiva resultava còmoda, encara que poc estimulant.
Què ens diuen aquestes troballes
Els resultats d'aquesta petita recerca confirmen una cosa que la bibliografia científica internacional ja fa anys que subratlla: la cultura d'aula condiciona la relació de l'alumnat amb les matemàtiques. Un enfocament basat en la resolució de problemes no sols proporciona aprenentatges significatius, sinó que també fomenta emocions positives i reforça la confiança en les pròpies capacitats. Al contrari, tornar a un model instrumental pot erosionar aquest vincle, especialment en els qui han descobert que les matemàtiques poden ser alguna cosa més que comptes.
Aquest article està basat en una recerca en què ha col·laborat Manuel Jesús Siaba-Lestón, mestre en el CEIP Plurilingüe Ricardo Tobío, Esteiro-Murs (la Corunya).
Pablo Beltrán-Pellicer, Profesor del área de Didáctica de la matemática, Universidad de Zaragoza; Gregorio Morales Ordóñez, Professor de Matemàtiques, Universitat de València i Sergio Martínez-Juste, Profesor de Didáctica de las Matemáticas, Universidad de Zaragoza
Aquest article es publicà originalment en The Conversation. Llegiu l'original.

.jpg)








