Complementos
MODELO LINEAL
Puede definirse como un esquema de relación entre una variable Y (EXÓGENA O A EXPLICAR) y otra(s) variable(s) X (X1X2 ... Xk ) (endógena(s) o explicativa(s), tal que:
Y= F.LINEAL (X) + PERTURBACIÓN ALEATORIA
(Modelo Lineal Simple)
Y= F.LINEAL (X1X2 ... Xk ) + PERTURBACIÓN ALEATORIA
(Modelo Lineal General)
Las hipótesis (básicas) que se asuman sobre la perturbación aleatoria permitirán realizar el análisis estadístico inferencial
Las razones para la introducción de una perturbación aleatoria, son fundamentalmente:
UTILIDADES DEL MODELO LINEAL:
1.verificar la existencia de la relación lineal.
2.estimar (contrastar) la (una) relación lineal concreta (estructural).- supone actuar sobre los coeficientes de la relación lineal.
3.predecir la variable y en función de x o (x1x2 ... xk )
ESPECIFICACIÓN DEL MODELO
NOTACIONES ALTERNATIVAS:
La información recogida hace referencia a n periodos de tiempo, o n localizaciones espaciales.Entonces, la relación (teórica) según el modelo entre las variables sería:
M.L.S.: yi= a + b xi + ei para i= 1,2,3,..., n
M.L.G.: yi = b0+ b1x1i + b2x2i + . . . + bkxki+ ei para i= 1,2,...,n
puede expresarse también matricialmente:
y = Xb + e donde:
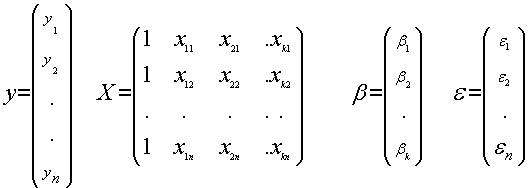
Y EN EL Modelo lineal simple
HIPÓTESIS BÁSICAS DEL MODELO LINEAL
Sobre el modelo lineal:
M.L.S.:
yi= a + b xi + ei para i= 1,2,3,..., n
M.L.G.:
yi = b0+ b1x1i + b2x2i + . . . + bkxki+ ei para i= 1,2,...,n
que también pueden expresarse matricialmente como: y = Xb + e
que establece la relación teórica entre las n observaciones de variable exógena y las de la(s) endógena(s).
Consideramos además las siguientes hipótesis básicas:
1ª " i ei sigue una N (0, s ) las perturbaciones aleatorias se distribuyen normalmente con media cero y desviación típica (varianza) constante (homoscedasticidad) en todos los periodos o localizaciones considerados.
2ª " i ¹ j D(ei ej) = 0 Las n perturbaciones aleatorias están incorrelacionadas ( al ser normales, son independientes).
(hipótesis de no autocorrelación)
Como consecuencia de estas dos hipótesis: e sigue una Nn(0; s2 I)
3ª La variable x (las variables x1,x2, . . .,xk) es (son) de naturaleza no aleatoria. Además sus valores son independientes de la perturbación aleatoria.Y en el caso del M.L.G. las variables x1,x2, . . .,xk están incorrelacionadas (hipótesis de ausencia de multicolinealidad)
Como consecuencia de estas hipótesis tendremos que el comportamiento teórico de las observaciones de y deberá ser tal que:
yi sigue una N(a + bxi; s ) con D(yiyj) = 0 " i ¹ j en el M.L.S.
yi sigue una N(b0 + b1x1i+ . . . + bkxki ; s ) con D(yiyj) = 0 " i ¹ j en el M.L.G.
y por lo tanto, para cualquiera de los dos casos la distribución conjunta del vector
de observaciones:
y sigue una Nn( Xb ; s2 I )
A partir de estas hipótesis podremos considerar que los valores observados de la variable y son "como si fueran" datos muestrales de una población normal de las características señaladas arriba y podremos plantearnos realizar inferencias sobre los parámetros (a,b y s ,en el M.L.S. o b0,b1, . . .,bk y s en el caso del M.L.G.)
ESTIMACIÓN DEL MODELO Y PREDICCIÓN PUNTUAL
Nos plantemos, en primer lugar construir un estimador del modelo (esto es , del valor teórico de yi) con la pretensión fundamental de obtener a partir del modelo estimado predictores puntuales de y para situaciones no observadas (supuestos ciertos valores de x).
Vamos buscando un estimador del tipo:
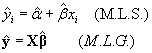
Empleando el método de máxima verosimilitud para obtener los E.M.V. de a,b,s en M.L.S. tendremos que:
La función de densidad de cada dato yi será:
![]()
y por tanto la f. de verosimilitud para el
conjunto de los n datos : ![]()
Tomando logaritmos e igualando a cero las derivadas parciales con respecto a a,b,s obtendríamos los tres E.M.V:
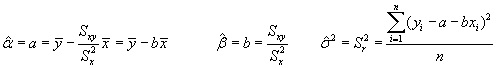
Es decir, se obtiene como resultado de la estimación máximo verosímil que los estimadores de los parámetros son los coeficientes de la regresión mínimo cuadrática y el estimador de la varianza de la perturbación, la varianza residual muestral.
Quedando el modelo estimado como: ![]()
y el predictor para un periodo
extramuestral: ![]()
Puede probarse que el E.M.V. del vector de parámetros b del M.L.G.también coincide con el vector obtenido por ajuste mínimo cuadrático:
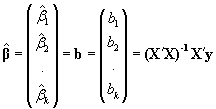
Siendo también la varianza residual muestral el E.M.V. de la varianza de la perturbación
DISTRIBUCIONES DE LOS ESTIMADORES
Con el objeto de poder realizar inferencias (estimaciones por intervalo y contrastes de hipótesis) sobre los parámetros analizaremos las distribuciones que tienen los estimadores obtenidos (E.M.V coincidentes con los E.M.C.O.)
Consideramos los estimadores del M.L.G. que luego particularizaremos para el M.L.S..Llamemos al estimador del vector (parámetros) b; b.
El vector b de estimadores (M.C./M.V.) es como sabemos:
b= (X'X)-1X'y
Esto es,será una función lineal del vector aleatorio n-dimensional y . Como el vector y sigue una Nn (Xb ;s2 I) la distribución de b será normal y como es un vector formado por k+1 (número de variables + 1) estimadores: la distribución de b será normal (k+1)-dimensional.
Su vector de medias vendrá dado por:
E(b)=E[(X'X)-1X'y ]= (X'X)-1X' E(y)=
=(X'X) -1X'E(Xb+e) = b+ E(e) = b de modo que los estimadores de los coeficientes son INSESGADOS
Su matriz de varianzas vendrá dada por:
D2(b)= D2 ((X'X) -1X'y)=D2 [(X'X)-1X'(Xb+e)]=D2 [((X'X) -1 X'X b) +(X'X) -1 X' e ]=
D2 [(X'X)-1X'e] =(X'X)-1X' D2(e) [(X'X)-1X']'=(X'X) -1X' .D2(e). X(X'X) –1 =
=s2 .[ (X'X) -1X' I X(X'X) –1 ] = s2 . (X'X) -1
de forma que b ® Nk+1 [ b ; s2 (X'X)-1]
En el caso del M.L.S. el vector de estimadores era, como sabemos:
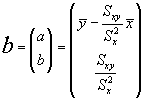
y la matriz (X'X)-1 era:
![]()
De modo que la distribución conjunta de los estimadores a,b será:
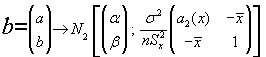
De donde obtenemos que :
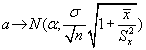
![]()
Siendo la covarianza entre ambos estimadores:
![]()
Para estudiar la distribución del estimador de s2 , la varianza residual que en el caso general para k variables (M.L.G.) tomaba la expresión:
Sr2= 1/n · S (yi- b0- b1x1- . . . - bkxk)2 =
=1/n · (y- Xb)'( y-Xb)
Consideraremos una variable derivada de este estadístico la variable:
nSr2/ s2= (1/s2 )S (yi- b0- b1x1- . . . - bkxk)2 =(1/s2) · (y- Xb)'( y-Xb)
Tengamos en cuenta que el vector de residuos muestrales ,e=y-Xb es un vector n-dimensional que se obtiene a través de una transformación lineal de dos vectores normales (y ý b):Por tanto su distribución será normal.
No es dificil probar que tiene por vector de medias el vector 0 y por matriz de varianzas la matriz M=[ I -X(X'X)-1X] que tiene por rango k+1 y la propiedad de ser idempotente MM=M'M=M.
Tampoco es costoso ver que la relación entre el vector de residuos muestrales y el de perturbaciones aleatorias es: e=Me
De esta manera que el estadístico nSr2/ s2 puede verse como:
nSr2/ s2=(1/s2) · (y- Xb)'( y-Xb)= (1/s2 ) .e'e=(1/s2 ) e'M'Me=
=(1/s2 )e'Me=(1/s2 ) (e'e) - (1/s2 )(e'X(X'X)-1X'e)
X'e es un vector aleatorio k+1 dimensional tal que X'e®N(0,s2(X'X))
de forma que,aplicando el teorema de Cochran:
1/s2 (e'e) sigue una chi2 con n grados de libertad
y 1/s2(e'X(X'X)-1X'e) sigue una chi2 con (k+1) grados de libertad
y a partir de este resultado es facil probar que:
nSr2/s2sigue una chi2 con (n -k-1) grados de libertad
(En particular para el caso del M.L.S k=1 ,de forma que:
nSr2/s2 sigue una chi2 con (n -2) grados de libertad)
Este último resultado es, no sólo importante en sí mismo sino que también tiene
efectos sobre las
inferencias de los estimadores de b.
En efecto, como sabemos b sigue Nk+1 [ b ; s2 (X'X)-1]
de modo que la distribución marginal de cada estimador de cada parámetro bj, bj será:
bj sigue N [ bj ; s ajj]
donde ajj es la raiz cuadrada de el elemento j-j de la matriz (X'X)-1
Como el parámetro s es desconocido es conveniente encontrar una distribución que no dependa de s .
Es fácil ver que el estadístico:
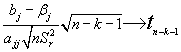
(Al valor que está dividiendo a la diferencia (bj-bj) se le llama error standard del estimador y se le suele representar por Sbj)
Lo que para el M.L.S. supone que:
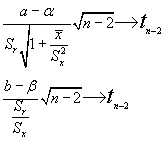
INFERENCIAS SOBRE EL MODELO LINEAL
Inferencia sobre un parámetro.
Contraste de hipótesis sobre un regresor.
Contrastes lineales sobre un conjunto de regresores.
Contraste de significación de los regresores.
Contraste de validez del modelo/ significación general/ Anova
Inferencias sobre un parámetro
Teniendo en cuenta los resultados anteriores resulta sencillo diseñar los métodos para la realización de inferencias sobre uno de los "regresores", bj .
Intervalo de confianza (1-a) para bj:
teniendo en cuenta que: 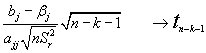
si llamamos Sbj al error standard del estimador ,esto es, a todo lo que divide a (bj-bj) en la expresión anterior; el intervalo de confianza para bj resulta (para un N.C. de 1-a):
bjÎ [bj - ta/2 Sbj ; bj + ta/2 Sbj] con (1-a) de confianza
Para el caso particular del M.L.S. los intervalos de confianza para los coeficientes a y b serán respectivamente:
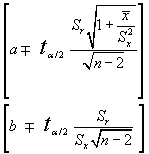
Ejemplo: En el ejemplo visto con anterioridad: El regresor para la primera variable explicativa (precio por kilo)e ra b2=-1.44765.La raiz cuadrada del elemento 2,2 de (X'X)-1, a22=(0.000746)1/2=0.027313,la "cuasi-desviación típica residual":Sr (n/n-k-1)1/2= 8.451406,de forma que que el error standard del estimador es: Sb2= 0.230912
Si queremos construir un intervalo de confianza para un nivel del 99%: t0.005 (12-2-1 g.l.)=3.25 de forma que el intervalo quedará:
b2Î [-1.44765- 3.25. 0.230912 ; 1.44765+ 3.25. 0.230912 ]
b2Î [-2.198114; 0.697186]
Contrastes de hipótesis sobre un regresor.
Basándonos en la distribución de (bj-bj)/ Sbj podremos igualmente contrastar hipótesis sobre el regresor bj
Si la hipótesis nula es: Ho: bj= bj* ya sea la alternativa uni o bilateral, el estadístico (bj-bj* )/ Sbj ,supuesta cierta la hipótesis nula tendrá una distribución t de Student(con n-k-1 g.l.) y podremos diseñar el contraste de la manera habitual que ya conocemos.
Contrastes lineales sobre un conjunto de regresores.
En muchos casos prácticos podemos estar interesado en contrastar una hipótesis no ya sobre el valor que toma un regresor,sino sobre cómo se comportan un conjunto de varios regresores.Si la hipótesis a contrastar consiste en que un conjunto de regresores verifican una cierta relación lineal esto puede llevarse a cabo a partir del procedimiento general que exponemos a continuación:
Una o varias relaciones lineales entre un
conjunto de regresores puede expresarse de forma general de la
siguiente manera:
Db = h
Donde el vector (k+1) dimensional b es el vector de parámetros (regresores) del modelo;h es un vector r-dimensional ,donde r es el número de relaciones lineales que estamos considerando; y, por último la matriz D de dimensión (r´k+1) es una matriz de coeficientes.
Así por ejemplo si queremos expresar sobre un modelo con 4 regresores (b0,b1,b2,b3)las siguientes 2 relaciones lineales:
b1+b2= 1 y b1-2b3= 0 podrá hacerse como:
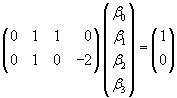
Teniendo en cuenta esto es facil ver que la hiótesis nula de que un conjunto de regresores verifican una o más relaciones lineales puede expresarse como:
H0: Db = h
Es igualmente sencillo probar que si pre-multiplicamos el vector de estimadores b por la matriz D el resultado será un vector aleatorio
r-dimensional cuya distribución será normal ya que es una transformación lineal (forma lineal) del vector b que seguía una distrución normal:
(b --> Nk+1[ b ; s2 (X'X)-1])
El vector de medias del vector Db será E(Db)=DE(b)=Db=h (siempre que la hipótesis sea cierta).
y la matriz de varianzas será
Var (Db)= D.Var (b) D'= s2 D(X'X)-1D'
Así pues, si la hipótesis nula es cierta: Db --> Nr [ h , s2 D(X'X)-1D']
Puede apreciarse que la distribución de este estadístico vectorial depende del parámetro desconocido s .Para evitar este problema puede actuarse de la siguiente manera:
Aplicando el teorema de Cochran es inmediato que la forma cuadrática:
1/s2. (Db-h)' [D(X'X)-1D']-1 (Db-h) sigue una c2 con r grados de libertad
Si consideramos que 1/s2 . e'e sigue una c2 con n-k-1 g.l.
y asumiendo la independencia entre ambas variables aleatorias:
el estadístico:
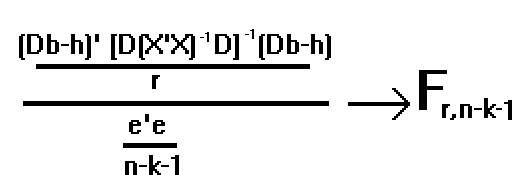
Bajo el supuesto de que la hipótesis nula es cierta.
Así pues evaluando este estadístico y comparandolo con el valor crítico correspondiente para el nivel de significación requerido:
si F > Fa rechazaremos la hipótesis que supone la presencia de esa relación lineal, y en caso contrario, la aceptaremos
Contrastes de significación de los regresores
Un tipo particularmente importante de contrastes de hipótesis sobre los regresores (ya sea sobre 1 o sobre varios de ellos) es el contraste de la hipótesis nula de que el (o los) regresor(es) considerado(s) son cero frente a la alternativa bilateral de que son distintos de cero.En estos casos, si llegamos a rechazar la hipótesis nula quedará establecido que el regresor es significativo queriendo decirse que existirá una relación lineal significativa entre la variable a explicar y la(s) variable(s) explicativa asociada al regresor (o regresores) sujeto(s) a debate.
Suele llamarse contraste de significación a este tipo de contraste.Cuando se trata de un contraste individual se llevará a cabo mediante un contraste t de Student bilateral.
Una medida de la significación o significatividad de un parámetro (regresor) suele darse a través del valor del nivel de significación necesario para rechazar la hipótesis de nulidad;de forma que cuanto más pequeño sea este valor más significativo es el regresor.
Un caso particular importante de los contrastes de significación es aquel en el que se consideran (a la vez)todos los regresores (excepción hecha del termino independiente).Este contraste constituye una prueba de la validez global del modelo y recibe el nombre de "contraste de significación general", de validez general (y, también de análisis de la varianza de la regresión)
Contraste de validez general (significación general)(ANOVA)
Como acabamos de comentar se trata de análizar la significación de todos los regresores a la vez, lo que equivale a analizar la validez general del modelo,la fuerza de la relación lineal existente entre la variable y y las variables x,la significación de la correlación lineal múltiple; todo ello es equivalente.
Como también hemos comentado se trata, en el fondo de contrastar la hipótesis:
H0: b1=b2=b3=. . . = bk= 0
Podemos plantearlo, exactamente igual que el contraste general de hipótesis lineales sobre un conjunto de regresores.
H0: Db = h
Aquí la matriz D sería la matriz identidad de orden k (con 1 elemento menos que el número total de parámetros k+1) y el vector h sería el vector 0 de orden k.
Pudiéndose expresar la hipótesis como:
H0:Ikb = 0k
y si llamamos b al vector de orden k formado por los regresores excluyendo el término independiente podemos expresar la hipótesis como: (igualmente a su estimador lo llamamos b y llamamos X a la matriz de los datos de x excluida la primera columna de unos)
H0: b= 0
Al ser la matriz D la identidad y el vector h el vector cero, el estadístico del contraste quedaría:
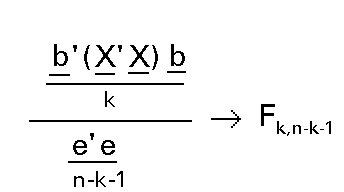
Si tenemos en cuenta que la regresión muestral era: Xb=y* y que pasaba por el centro de gravedad, entonces: b' X' X b será n veces la varianza debida a la regresión:
b' X' X b = n S2y*=n S2yR2 . (Donde R2 es el coeficiente de determinación muestral)
Por otro lado:e'e es n veces la varianza residual:
e'e= n Sr2 = n Sy2(1- R2).
A partir de estos dos hechos es muy facil ver que el estadístico del contraste queda como:
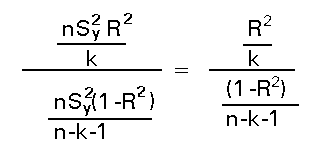
Que bajo el supuesto de la hipótesis nula seguirá una distribución Fk,n-k-1
Es interesante observar que en el caso del M.L.S. , con k=1, y ante la coincidencia del coeficiente de determinación y el cuadrado del coeficiente de correlación, nos encontramos con el estadístico del contraste de incorrelación, cuya distribución no probamos y aquí haya una demostración.
El planteamiento de este contraste admite un esquema ANOVA, en el siguiente sentido: La variación total (muestral) de la y (nSy2) puede descomponerse en variación debida a la regresión
( b'X'Xb = n S2y*=n Sy2R2 ) más la variación residual o no explicada
(e'e= n Sr2 = n Sy2(1- R2)).
PREDICCIÓN DE UN VALOR EXTRAMUESTRAL.-PREDICCIÓN POR INTERVALO
Ya vimos que la predicción puntual de un valor de y extramuestral se llevaba a cabo utilizando como predictor el modelo estimado aplicado sobre los valores futuros de las variables explicativas.
De manera general podríamos expresarlo de la siguiente forma:
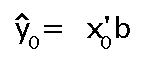
Donde x'0 es el vector fila formado por los valores futuros de las variables explicativas: x'0 = ( 1 x10 x20 . . . xk0 )
Este predictor es una transformación lineal del vector aleatorio b de los estimadores del vector de regresores b .Ademas la dimensión del predictor es 1, por lo que será una variable aleatoria Normal.
Ademas su media será: E(x'0 b)= x'0 E(b) =x'0 b esto es, el valor teórico esperado en el futuro para la variable y (el predictor es insesgado).
Por otro lado su varianza será:
Var(x'0b)=x'0 Var(b)x0 = s 2 x'0 (X'X)-1x0
Así pues la distribución del predictor es:
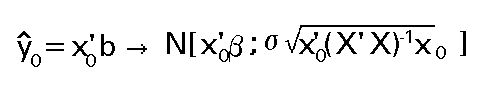
Distribución que depende del parámetro desconocido s .Este problema puede solventarse construyendo el estadístico
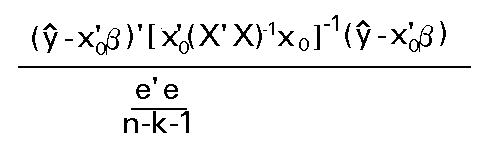
Que tendrá una distribución F de Snedecor con 1 y n-k-1 g.l..
Como tanto x'0 (X'X)-1x0 ; como x'0b ; como el predictor son escalares podemos expresar este estadístico como:
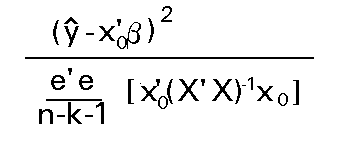
Y como la raiz cuadrada de una variable F1,n-k-1 es una variable t de Student con n-k-1 g.l., tendremos que:
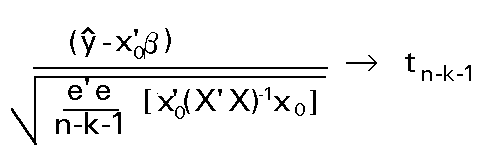
A partir de este estadístico es sencillo construir un intervalo para la predicción esperada según el modelo, dado un nivel de confianza prefijado (1- a):
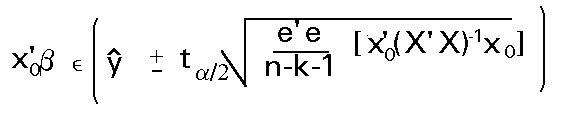
Donde ta/2 es el correspondiente valor
tabulado para n-k-1 g.l.
Es interesante ver cómo quedaría el intervalo de predicción en el caso de un M.L.S.:
Tras realizar las operaciones pertinentes acaba quedando un intervalo para el valor futuro de y (teórico según el modelo):
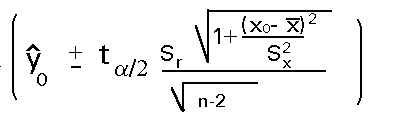
Donde ta/2 es el valor tabulado para n-2 grados de libertad.
COMPLEMENTOS
ESPECIFICACIÓN DEL MODELO
NOTACIONES ALTERNATIVAS:
La información recogida hace referencia a n periodos de tiempo, o n localizaciones espaciales.Entonces, la relación (teórica) según el modelo entre las variables sería:
M.L.S.: yi= a + b xi + ei para i= 1,2,3,..., n
M.L.G.: yi = b0+ b1x1i + b2x2i + . . . + bkxki+ ei para i= 1,2,...,n
puede expresarse también matricialmente:
y = Xb + e donde:
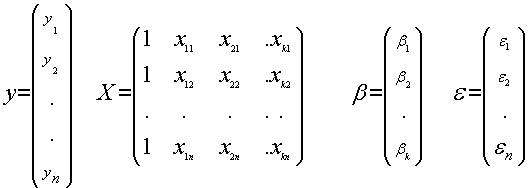
Y EN EL Modelo lineal simple
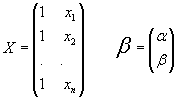
FORMA LINEAL:
sea a un vector columna de constantes de Rn
sea x un vector columna de variables de Rn
una forma lineal es entonces f(x)= x' a = a' x = S ai xi
FORMA CUADRÁTICA:
Si A es una matriz cuadrada de orden n
una forma cuadrática es entonces:
Q(x)= x' A x = S S aij xi xj
Tanto f como Q son funciones que hacen corresponder vectores de Rn con valores (escalares) de R.
DERIVACIÓN VECTORIAL DE F. LINEALES Y CUADRÁTICAS:
puede probarse que la derivada vectorial de una f. lineal es:
![]()
y que la derivada vectorial de una forma cuadrática es:
![]()
EN EL CASO DE QUE A SEA UNA MATRIZ SIMÉTRICA:
( A' + A)= 2A Y LA DERIVADA RESULTA SER: 2Ax
CUESTIONES PREVIAS SOBRE LA REGRESIÓN (MUESTRAL) MÍNIMO-CUADRÁTICA:
Recordemos que el método de ajuste por "mínimos cuadrados "a una
recta y= a + b x se basaba en obtener como coeficientes a,b aquellos valores que :
min j (a,b)= min S (yi- a - bxi)2
y que el resultado de tal ajuste acababa
siendo:
![]()
Igualmente para el caso multidimensional la ecuación de ajuste mínimo cuadrático y = b0+b1x1+. . . +bkxk
que matricialmente puede expresarse (si la extendemos para los n datos disponibles) como: y= Xb
la podremos obtener
min j ( b0,b1, . . . ,bk) = min S (yi- b0- b1x1- . . . - bkxk)2
esto es: min j ( b)= min (y - Xb )' (y - Xb )
de forma que el vector de coeficientes b que nos dará la ecuación de ajuste mínimo-cuadrático será tal que igualará a cero la derivada parcial de j ( b) con respecto a b :
j ( b)= (y - Xb )' (y - Xb ) = y'y - (Xb)'y - y'(Xb)+(Xb)'(Xb) =
= y'y - b'X'y - y'X b + b'X'X b = y'y - 2 b'X'y + b'X'X b
por lo que la derivada parcial de j ( b) con respecto a b acaba siendo:
-2 X'y + 2 X'X b que si la igualamos a cero nos dará la solución del ajuste mínimo-cuadrático:
-2 X'y + 2 X'X b= 0 Û b= (X'X)-1 X'y
de forma que el vector de coeficientes que nos da el ajuste a un hiperplano que minimiza la suma de los cuadrados de los residuos es:
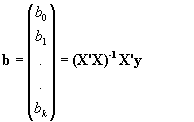
es facil comprobar que en el caso de la regresión simple los coeficientes de la recta de regresión mínimo-cuadrática verifican también esa relación:
en efecto en el caso de la regresión simple tenemos:
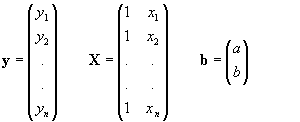
de manera que X'X será:
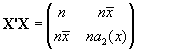
y su inversa (X'X )-1 =
![]()
y por otro lado X'y sera:
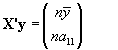
por lo que el vector (X'X)-1 X'y acaba siendo:
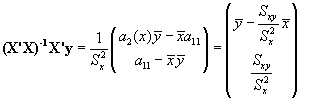
es decir los valores de los coeficientes a y b que ya conocemos.
RECORDEMOS, en otro orden de cosas,que la VARIANZA RESIDUAL era uno de los indicadores de la calidad del ajuste tanto en el caso de la REGRESIÓN SIMPLE como de la LA MÚLTIPLE, y se definía como: Sr2= 1/n · S (yi- a -bxi)2 en el caso de la R.simple
Sr2= 1/n · S (yi- b0- b1x1- . . . - bkxk)2
en el caso de la R. múltiple
y matricialmente Sr2= 1/n · (y- Xb)'( y-Xb)
En el caso de la regresión simple : Sr2= Sy2(1 - r2) = Sy2 - r2.Sy2
y en el caso de la regresión múltiple: Sr2= Sy2 (1 - R2) = Sy2 - R2.Sy2
donde r y R son respectivamente el coeficiente de correlación entre x e y y el coeficiente de correlación múltiple entre y, y las xi (a sus cuadrados se les llama coeficiente de determinación)