
Anabel Forte Deltell, Universitat de València
Catorze de març: 14/3 o 3/14, si ho llegim en nomenclatura anglosaxona. En dir “tres catorze”, ràpidament es dibuixa en el nostre pensament un nombre que ens recorda l'institut. És molt possible, a més, que en sentir-lo, continuem la tirallonga: quinze, noranta-dos, seixanta-cinc… fins on ens arribe la memòria per a recordar les xifres del singular nombre pi.
El 2009, el Congrés dels EUA declarà oficialment que aquest dia, el 14 de març, seria el Dia de π. Tingué un enorme èxit des del seu inici, i la idea cresqué fins que el 2019 la UNESCO el declarà el Dia Internacional de les Matemàtiques. Des d’aleshores, cada any més i més gent s'ha anat incorporant a la celebració, amb π com a símbol dels qui estimem les matemàtiques.
Pi no és realment un nombre
Comencem per aclarir un fet: pi és la setzena lletra de l'alfabet grec (π) i en matemàtiques la usem per a representar una cosa molt més interessant que un nombre (que no dic jo que els nombres no ho siguen). Així doncs, la primera raresa de pi és aquesta: que no és un nombre. Però llavors, si no és un nombre, què és pi?
Pi representa la proporció que manté la longitud de la circumferència amb el seu diàmetre. Una proporció que té la particularitat (ací, la seua segona raresa) de ser constant, això és, de valer sempre el mateix sense importar com de gran o de petita siga la circumferència.
En particular, en la geometria euclidiana –la que devem a Euclides (325 - 265 abans de l’era comuna) i que ens assegura coses com ara que per dos punts passa una única recta– el valor constant de pi és tan especial (i ja en van tres) que fins i tot és irracional.
No és que haja perdut la raó sinó que, tot i ser el resultat de dividir el perímetre entre el diàmetre, no pot expressar-se mai com la divisió de dos nombres enters. Si el diàmetre d'una roda és un valor “exacte”, sense decimals, l'espai que recorrerà en fer una volta no ho serà. Però, aleshores quant serà? Ens acostem a una qüestió clau, el valor de pi… Però deixeu-me que abans continue amb una altra de les seues rareses, la quarta ja.
Pi és transcendent. No és que siga tan important perquè transcendisca ni perquè siga transcendental. Aquesta propietat matemàtica ens assegura que pi no serà mai la solució de cap polinomi. Polinomi? Segur que ho recordeu dels estudis de matemàtiques. Els polinomis són les equacions en les quals la incògnita apareix elevada a un o diversos nombres naturals, per exemple x2 + x + 3 = 0.
Doncs bé, és igual els exponents i els nombres que hi puguem posar: no hi ha un polinomi per al qual la x valga pi. Cal esmentar, a més, que aquesta és una propietat que no compleixen gaires nombres, de manera que, a hores d'ara, ja està demostrat que pi és raret, però encara falta la millor. Ara sí, parlarem del seu valor.
L'esmunyedís valor de Pi
Com dèiem a l'inici, el valor constant de pi (en la geometria euclidiana) és de 3,141592… però, precisament pel fet que és irracional, sabem que tindrà infinits decimals. Infinits, com sona, sense fi i, per a més inri, en aquest cas no sols és que siguen infinits, sinó que no segueixen cap patró. Semblen col·locats a l'atzar, amb totes les xifres del 0 al 9 tenint la mateixa probabilitat d'aparèixer. De fet, poden usar-se els seus valors com un generador de nombres aleatoris i és possible cercar-hi qualsevol sucessió de xifres, fins i tot el nombre de DNI d'una persona qualsevol, que de segur que s’hi troba en alguna banda. No obstant això, la cosa més important d'aquesta propietat de pi és que s'ha convertit en una font inspiració per al treball de moltíssima gent.
Des dels temps més remots (hi ha indicis que pi ja era conegut pels babilonis l’any 2000 abans de l’era comuna) s'han fet esforços per aconseguir establir-ne el valor amb la màxima precisió possible. En particular, un dels primers a donar fruit va ser el d'Arquimedes de Siracusa (287 - 212 a. e. c.), que va dissenyar un mètode per a delimitar el valor d'aquesta rara constant.
Arquimedes usava polígons que s'inscrivien (els que se situen dins de la circumferència) i se circumscrivien (els que contenen a la circumferència en el seu interior). D'aquesta manera, el valor del perímetre de la circumferència se situaria sempre entre el perímetre del polígon inscrit i el del polígon circumscrit. Afegint cada vegada més costats als polígons, Arquimedes va aconseguir donar un interval de valors per a pi, que tenia un error màxim del 0,040% sobre el valor real… Vaja, propet, ben propet.
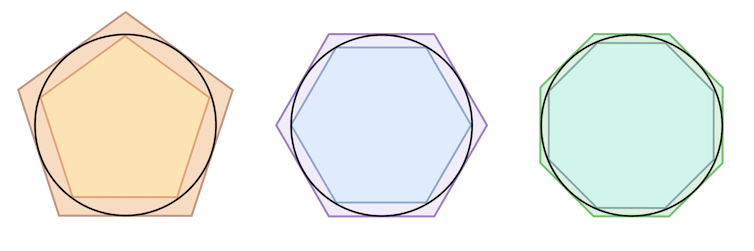
Mètode d’Arquimedes per a l'aproximació de pi. Wikipedia Commons
La idea d'Arquimedes va trobar seguiment en moltes altres i de molt diversa índole, algunes fins i tot des del punt de vista de la probabilitat i l'estadística, com va ser el cas de Georges-Louis Leclerc (1707-1788), el comte de Buffon.
En particular, Leclerc va trobar el nombre pi mentre tractava de determinar com de probable era que, en llançar una agulla sobre un conjunt de línies paral·leles, aquesta caigués travessada sobre una de les rectes. Després de diversos càlculs va arribar a la conclusió que, si les línies estaven separades per la mateixa distància que la longitud de l'agulla, aquesta probabilitat era de 2 dividit per pi. D'aquesta manera era fàcil aproximar pi llançant moltes agulles, observant la proporció d'aquelles que tallaven realment a les rectes paral·leles i comparant-la amb la probabilitat exacta.
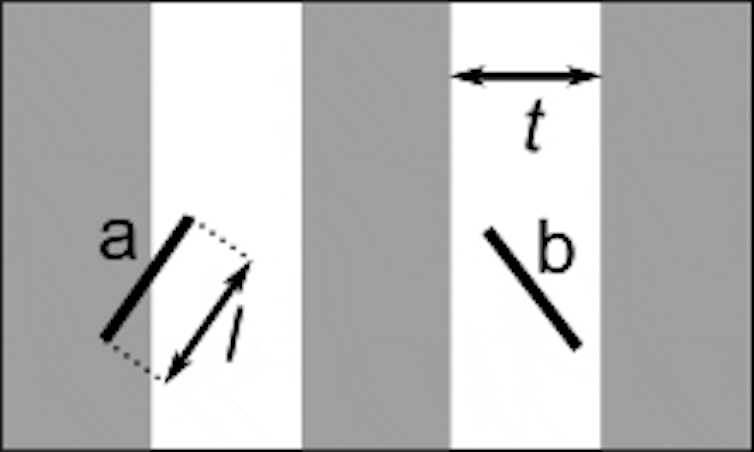
Buffon needle. Buffon_needle.gif: Claudio Rocchini, derivative work: Nicoguaro
Tot i això, amb l'arribada de l'era de la computació va aparèixer la cinquena raresa de pi: ser un nombre computable. En particular, Alan Turing, ja el 1936, va definir que un nombre és computable si existeix un algorisme que ens permet aproximar el seu valor amb una quantitat de xifres decimals predeterminades.
S'han calculat 63 bilions de decimals de pi
Seguint aquesta premissa, el 1949 una màquina ENIAC va aconseguir trencar el rècord establert fins al moment per l'ésser humà i calcular els 2037 primers decimals de pi, cosa amb la qual donava el tret d'eixida a una cursa que ha arribat fins als 63 bilions (europeus) de xifres amb les quals va ser calculat en 2021 per un equip de la Universitat de Ciències Aplicades del cantó suís dels Grisons.
Però pi no és només un entitat matemàtica curiosa que ha fet sonar les cordes del pensament humà des de l'antiguitat. Pi és, com assegura Rhett Alain, un nombre sorprenent que apareix de manera natural allà on menys l'esperem: en l'estimació de la nostra posició per GPS, en el moviment del pèndol d'un rellotge de paret o fins i tot en la manera en què un assistent per veu és capaç de reconèixer que, per exemple, l'usuari vol que li conte un acudit.
Però, sobretot, pi és l'excusa perfecta perquè cada catorze de març celebrem les matemàtiques i tot el que ens donen. Bon Dia Internacional de les Matemàtiques!
Anabel Forte Deltell, Doctora en Matemàtiques i professora en la Universitat de València, Departament d'Estadística i Investigació Operativa, Universitat de València
Este artículo fue publicado originalmente en The Conversation. Lea el original.

.jpg)








